1. 引言
随着经济的发展以及人们对环境问题的日益关注,清洁能源的地位不断提升。近些年来,中国的清洁能源发展非常迅速,而风电作为重要的清洁能源之一,其在经济和环境上有着巨大优势,有关风电的各方研究也日益增多。但风电出力具有明显的波动性和反调峰特点,风力发电大规模并网后功率的时域波动会造成电网调峰能力不足,影响电力系统的稳定运行,在负荷的低谷期,系统调峰容量不足也将产生弃风问题。
此外,由于其良好的环境效益,电动汽车在近几年得到国家的大力支持和发展。随着电动汽车技术的发展,特别是性能卓越的电池和充电性能卓越的电机及其控制系统的飞速发展,电动汽车的发展明显加快。在电动汽车的行驶过程中,碳的排放量取决于一次能源结构,而中国的能源结构还是主要以火电为主,因此电动汽车的单位里程碳排放水平在某些情况下甚至有可能高于传统汽车,大大限制了电动汽车的减排能力。此外,受车主出行习惯的影响,电动汽车大量入网后负荷高峰时段充电,也将会增大峰谷差和系统压力。大量电动汽车的无序充电行为会影响系统的安全性与可靠性。
现阶段国内外已经开展了很多研究。文献 [1] 提出电动汽车与风力发电的协同调度策略,通过对电动汽车充电的调度来调节峰谷差,消纳更多的风电。文献 [2] 分析了电动汽车充电在低碳电力系统中可以充当的角色和作用。文献 [3] 分析了电动汽车代替传统汽车来达到碳减排目的的策略。文献 [4] 以碳排放最少为调度目标,分析了在对电动汽车充电进行合理调度下的碳减排效益。文献 [5] 考虑需求响应,将用户成本考虑到模型中,提出了一种负荷方差最小且火电和用户成本最低的电动汽车充电策略模型。文献 [6] 以最大限度改善负荷方差、排放最小以及火电成本最低为目标对电动汽车充电进行优化调度。文献 [7] [8] [9] [10] [11] 考虑用户侧的利益,提出分时电价的制度,同时考虑平滑负荷波动,减小负荷峰谷差。文献 [12] 基于分时电价,提出了寻找负荷最低时段和倒序逆推两种充电模式。文献 [13] 提出基于分时电价的一种滚动优化控制策略,并与无序充电对比,结果能有效降低用户成本和达到削峰填谷的目的。文献 [14] 研究了虚拟电厂的碳减排策略。文献 [15] 提出一种双层调度模型,在上层考虑用户利益,在下层考虑用户满意度,并尽量与上层模型偏差最小。文献 [16] 利用虚拟电厂的概念,将电动汽车、火电以及清洁能源作为一个整体,对电动汽车的充电进行调度,以收益最大为目标并将碳交易的概念加入其中。可以看出,对电动汽车充电和风电的协同调度能够良好的解决上述问题,不过目前的研究停留在考虑峰谷差、发电成本或是用户成本,而忽略了碳减排的效益,或是单一的考虑碳排放这唯一条件。
本文在考虑降低等效负荷方差的基础上,以碳排放最低和系统成本最低为目标,并加入碳交易机制,充分分析调度策略的碳减排水平,并赋予碳减排经济价值。
2. 电动汽车全生命周期碳排放水平
为了核算有电动汽车参与调度的系统碳排放水平,并与燃油汽车和无序充电下进行比较,不能忽略电动汽车生命周期中产生的碳排放量,使用全生命周期法对电动汽车生命周期的碳排放量进行核算。生命周期法即详细研究产品生命周期内各单元过程的能源需求、原材料利用和活动可能造成的污染排放。将电动汽车的生命周期分为三个过程,生产、使用以及报废 [17] 。在生产阶段,又分为传统汽车制造部分以及锂电池制造部分。在使用阶段,电动汽车的碳排放主要取决于一次能源的类型以及其对环境的影响。在报废阶段,主要分析汽车材料的报废和回收对环境所产生的影响。对比电动汽车的生命周期与燃油汽车的生命周期,可以发现,最主要的区别在于锂电池的制造以及行驶过程中的碳排放,在本文中,为了对比燃油汽车与电动汽车的碳排放,所以重点分析生命周期中的这两个部分。
锂电池制造阶段,主要消耗的能源为电能,将制造过程分为两个部分:原材料制备和电池组装。在原材料制备过程中,耗电量主要根据各原材料制造的耗电量加权平均来计算,权重为电池中对应含量。由于材料比较复杂,采取抓大放小的思路,主要取锂电池中国产的能耗大含量大的原材料。其公式如下:
(1)
其中
代表材料制造总过程中的电耗,
代表第i种材料电耗,
代表该材料的含量比重。这里主要取正负极材料以及铜箔和铝箔。
在组装过程中,因为工艺复杂繁多,无法详细确定单个工序电耗,所以采用整体测算,取组装厂年度耗电总量,除以产品总重量,得到单位质量锂电池组装的耗电量,如下:
(2)
其中,
代表单位质量电池组装耗电量,
为年度耗电总量,M为产品总质量。
最后将耗电量折算成标准煤,公式如下
(3)
式中,
代表锂电池的煤当量,
为折算系数。
根据文献 [17] 提供的数据得生产1吨电池排放二氧化碳约23.71吨。
电动汽车行驶过程中的碳排放量取决于电耗量以及一次能源对环境的影响,在电动汽车与风电协同调度中,一次能源主要为火电以及风电,在下文,结合实际情况对其进行分析和计算。
为了使锂电池生产中的碳排放量和下文行驶过程中的碳排放量相结合,将其归算到行驶里程中,假设电动汽车全生命周期行驶里程为150,000 km,电池循环次数达10年以上,设定电动汽车生命周期只需要一组电池。E150V型电动车电池重量约为300 kg。本文将其归算到电动汽车充每度电排放的二氧化碳量,公式如下:
(4)
其中,
代表总的碳排放量,
为总行驶里程,W为百公里耗电量,
代表充电效率。求得数值约为351.26 t/Gwh。
3. 电动汽车充电负荷建模与风电出力建模
首先对电动汽车充电负荷进行建模,假设开始充电时刻、初始SOC、目标SOC之间相互独立。
根据数据统计,电动汽车开始充电时刻近似为正态分布 [18] 。其概率密度函数如下:
(5)
其中
,
,
,
。
电动汽车到达充电站开始充电时车载电池的初始SOC及充电结束时的目标SOC都与起始充电时刻一样,也具有一定程度的随机性,本文均使用概率模型对其进行描述,公式如下:
(6)
(7)
其中,
为初始S0C,通常在0.1~0.6之间。
为目标SOC,通常在0.5~1.0之间。
,
,
,
。
本文假设电动汽车都以恒定功率充电,取充电功率为100 KW。因此,根据充电功率以及初始SOC、目标SOC,可以计算出充电时长,再根据上述模型模拟出各时段电动汽车充电数量,进而得到各时段充电负荷。
其次对风电出力进行模拟,这里选用双参数威布尔风速模型,公式如下:
(8)
式中,k和c为威布尔分布的形状参数和尺度参数。
结合威布尔风速模型,假设空气密度恒定,线性化有功出力曲线,得出风电出力分段函数:
(9)
式中,
、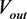 和
分别对应风电机组的切入风速、切出风速和额定风速;
为风电机组的额定有功出力。当风速大于
时,风电机组启动并正常运行;当风速大于
且小于
时,风电机组有功出力保持额定值;当风速小于
或大于
时,风电机组停止运行。
和
分别对应风电机组的切入风速、切出风速和额定风速;
为风电机组的额定有功出力。当风速大于
时,风电机组启动并正常运行;当风速大于
且小于
时,风电机组有功出力保持额定值;当风速小于
或大于
时,风电机组停止运行。
4. 电动汽车-风电协同调度建模
4.1. 目标函数
本文主要考察电动汽车的碳减排效益,因此以碳排放量最小为目标函数,在这里主要考虑火电本身的碳排放,以及电动汽车全生命周期核算过后对应到充电上的碳排放量,如下:
(10)
其中,
表示火电的碳排放因子,
代表第t时段的火电出力,
为第t时段电动汽车充电功率。
其次考虑系统成本最低,系统成本分为两部分,一部分是火电机组运行成本,主要由发电成本构成,另一部分为碳交易成本,采用基准线法,根据出力分配碳排放配额,超出配额的碳排放部分需要支付额外的费用,相反,多余的部分可以获得相应的收益 [16] 。由此目标函数如下:
(11)
其中,
为t时刻的火电机组运行成本,
为t时刻的碳交易成本。
火电机组运行成本表示为:
(12)
其中
、
、
为第i台发电机的发电成本系数。
碳交易成本如下:
(13)
(14)
其中,K为碳交易价格,
为t时刻系统的实际碳排放量,
为t时刻碳排放配额。
为配额系数。
最后,风电与电动汽车的协同调度目的之一是为了削峰填谷,缓解系统调峰压力。因此,定一个M个时段为一个时间窗口,使每个时间窗口等效方差最小(1),其公式如下:
(15)
(16)
其中,
为t时刻风电出力,
为t时刻常规负荷。
为第i个时间窗口等效负荷的平均值。
4.2. 约束条件
1) 系统约束
系统要满足负荷和出力的平衡,如下:
(17)
2) 电动汽车充电约束
每个时段的电动汽车充电负荷要小于该时段可调度的电动汽车充电负荷,约束如下:
(18)
其中,
为t时段电动汽车可调度充电功率的上限。
另外,为了保证电池寿命,防止深度充放电,应保证电量有一定余额,并小于电池容量上限,其约束如下:
(19)
其中,
,
为电池储存容量的上下限。
为t时刻电池剩余电量。
最后,协同调度下电动汽车总的充电需求应该大于等于电动汽车自由充电时充电需求和,约束如下:
(20)
其中,
为电动汽车自由充电时充电需求的总和。
3) 火电机组出力约束
a) 出力约束
每台火电机组出力应该介于其上下限之间,如下:
(21)
其中,
、
为第i台火电机组出力的上下限。
b) 爬坡约束
火电机组出力的上升或下降速率有其极限值,如下:
(22)
其中,
、
为i机组的最大滑坡和爬坡功率。
c) 风电出力约束
(23)
其中,
为t时刻风电出力的最大值。
4.3. 模型求解
本文主要采用多目标粒子群优化算法。粒子群算法模拟鸟集群飞行觅食的行为,通过鸟之间的集体协作使群体达到目的。多目标粒子群算法是基于粒子群算法的改进。在算法中加入非支配关系排序、粒子拥挤距离计算以及锦标赛选择,最终获取粒子的Pareto前沿 [19] 。
多目标粒子群算法的基本流程如下:
1) 随机初始化种群,设定惯性权值。
2) 求解粒子的各目标函数值。
3) 按照适应度对粒子进行非支配排序。
4) 计算各粒子的拥挤距离。
5) 根据粒子的前沿等级和拥挤距离,使用锦标赛选择法选取种群的个体最优和全局最优。
6) 按照下式更新粒子:
(24)
(25)
是粒子的速度,pbest和gbest是粒子的个体最佳和全局最佳位置,rand代表0~1之间的随机数,c1、c2是学习因子,ω代表惯性权值。
7) 重复2~6过程直至满足迭代条件。
在Pareto集中挑选最优粒子,使用模糊理论求解。本文追求碳排放最小和成本最小,选用偏小型模糊隶属度函数(5)。
(26)
(27)
其中,
等于0和1时代表对目标i函数值的完全不满意和满意,
为目标函数值。采用式(27)求得Pareto解集中的标准化满意度,然后通过式选取最大
值的Pareto解作为最优解。
5. 算例分析
本文考虑风机装机容量10 GW,负荷数据参考文献 [4] ,火电机组成本参数参考文献 [20] ,折算燃煤价格,碳排放配额系数取0.8112 kg/kwh,碳价格为0.25元/kg,考察时段为24小时。根据第二节风电出力概率模型得24小时风电功率如图1。
假设电网在负荷方差过大会选择弃风,根据电动汽车自由充电和协同调度充电模型计算结果分析。得到合理的自由充电曲线图2,协同充电曲线如图3。
可以看出,在满足一定充电需求的情况下,对电动汽车充电进行协同调度后,能有效减少峰谷差,平衡负荷曲线,同时也提高了风电利用率。

Figure 1. 24-hour wind power output curve
图1. 24小时风力发电出力曲线
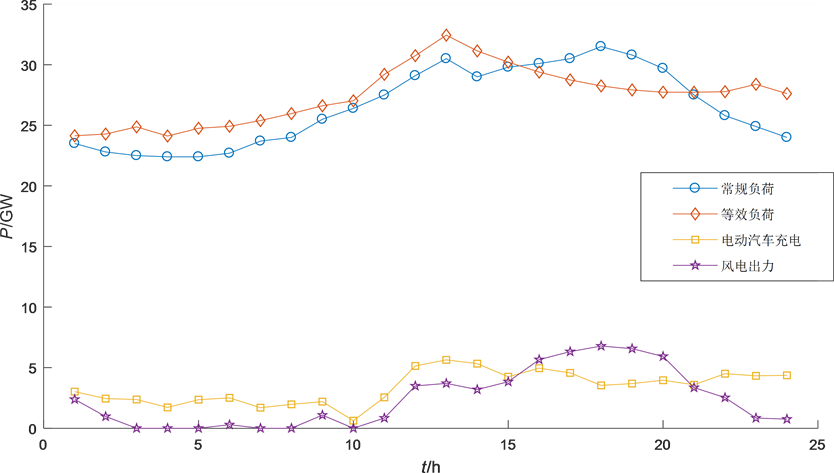
Figure 2. Free charge of electric cars
图2. 电动汽车自由充电
Figure 3. Coordinated charge of electric cars
图3. 电动汽车协同调度充电
两种充电模式下,系统的等效负荷方差、单位电量碳排放量、发电成本包括碳交易成本对比如表1。
可以看出,在协同调度下,系统的碳排放量大大降低,并且由于碳交易机制的加入,系统的发电成本也得到了大幅度的降低。EV150电动汽车25度电可以行使150 km左右,根据系统单位电量的碳排放量核算到电动汽车行驶单位里程的碳排放量为0.184 kg/km,一辆小型纯燃油汽车单位里程碳排放量为0.192 kg/km,可以看出电动汽车在节能减排方面的确存在着优越性。

Table 1. Comparison of free charge and co-charge
表1. 自由充电与协同充电数据对比

Table 2. Carbon emissions per mile of different wind power capacity
表2. 不同风电装机容量比下电动汽车单位里程碳排放
在本场景下,改变风电机组的装机容量与火电机组装机容量的比例,折算到电动汽车单位里程碳排放量如表2。
可以看出在纯火电系统中,电动汽车的碳排放量甚至高于传统的燃油汽车,在协同调度策略下,风电并网的容量越大时,才越能体现电动汽车在节能减排上的优越性。
6. 结论
本文建立了低碳经济下的风电与电动汽车充电协同调度模型,并对模型进行了仿真验证。在核算电动汽车全生命周期过程碳排放的基础上,对比了自由充电、协同调度下电动汽车碳排放以及燃油汽车的碳排放,可以看出协同调度在消纳风电,平缓负荷曲线的同时,在环境和经济效益上也有巨大的优势。此外,在一定情况下,电动汽车单位里程碳排放甚至高于燃油汽车,因此,保证清洁能源的利用率对电动汽车是否真正减排具有重大意义。
基金项目
国家电网公司总部科技项目“基于能源互联网的电动汽车新一代充放电关键技术研究与示范”资助。
参考文献