低渗–致密气藏压裂井产能理论计算方法

Study on Productivity Calculation Model of Fractured Well in Low Permeability-Tight Gas Reservoir

摘要: 目前越来越多的低渗致密气藏投入开发，但由于自然产能低，需人工压裂。很多学者针对低渗压裂井产能进行了研究，但并没有学者同时考虑低渗致密气藏储层存在的应力敏感性、气体通过低渗致密多孔介质同样具有启动压力梯度以及人工裂缝近井地带存在高速非达西效应等因素对产能的影响，因而计算结果往往偏大。本文以扰动椭圆以及发展的矩形族思想为基础，理论推导出考虑因素更全面的低渗致密气藏压裂井产能理论计算公式，并绘制了相应的产能曲线。研究表明，拟启动压力梯度、变形介质系数、高速非达西渗流因子以及裂缝参数均对低渗致密气藏压裂井产能有影响，并绘制了单因素敏感性分析图版，研究结果具有较高的理论价值和实践指导意义。

Abstract: With the development of more and more low-permeability tight gas reservoir, hydraulic fracturing is needed due to the low natural productivity. Productivity of low permeability fractured well has been studied by many scholars, however, the calculation result is usually large while the influencing factors of productivity are not simultaneously considered, including the stress sensitivity, threshold pressure gradient with gas flow and high-speed non-Darcy effect of hydraulic fracture near the well. In this paper, on the basis of disturbing ellipse and rectangular family, the productivity calculation formula of fractured well in low permeability tight gas reservoir is derived theoretically with consideration of more factors and the corresponding productivity curve is plotted. Result shows that, the influencing factors of fractured well productivity in low permeability tight gas reservoir include threshold pressure gradient, deformed media coefficient, high-speed non-Darcy flow factor and fracture parameters. Single factor sensitivity analysis plate is also protracted, which has important theoretical value and practical meaning.

1. 引言

低渗致密气藏由于孔喉致密，比表面大，导致气体在低渗致密多孔介质渗流时同样存在启动压力梯度，同时储层存在应力敏感性。一般来讲，低渗致密气藏自然产能低，往往需要通过人工压裂来提高产能，导致气体在压裂裂缝中流速很高，近井地带惯性效应不可忽略 [1] ，不再符合经典的达西定律。由此可以看出，低渗致密气藏压裂井涉及到的渗流机理十分复杂，开展低渗致密气藏垂直裂缝井的产能计算对指导该类气藏的有效开发具有十分重要的意义。目前诸多学者对低渗致密气藏的产能进行了研究和计算，罗天雨等学者 [2] 将气井压裂后的渗流分为裂缝区域外拟径向渗流以及近裂缝的单向非达西渗流，并给出了相应的产能方程。蒋廷学和汪永利等学者 [3] 采用保角变换方法分别研究了油藏和气藏垂直裂缝井产能计算方法；杨正明 [4] 等将气井压裂后气体流动考虑为径向流和线性流的组合，并给出了产能计算公式；周琦 [5] 、雷刚 [6] 等学者也对低渗透气藏压裂井产能进行了研究；总结来看，低渗致密气藏压裂井产能计算方面取得了一定研究成果，但普遍存在着推导过程中进行了一定程度的简化，导致预测结果可能偏大。本文基于扰动椭圆概念以及等价的发展矩形族思想 [7] ，给出了同时考虑上述因素的低渗致密气藏压裂井的产能计算方法，并进行了相应的敏感性分析，总结了拟启动压力梯度、变形介质系数、高速非达西渗流因子以及裂缝参数对产能的影响规律，具有较高的理论价值和实践指导意义。

2. 低渗致密气藏复杂渗流机理表征方法

诸多学者的研究表明，经典的达西定律有一定的适用条件。低渗致密气藏由于孔喉致密，比表面大，固相岩石颗粒对渗流的影响难以忽略，需要考虑启动压力梯度。同时诸多学者的研究表明气体在低渗致密多孔介质中渗流时，由于滑脱效应(又称Klinkenberg效应 [8] [9] )使得储层视渗透率增大，但由于其对产量的影响一般小于启动压力梯度对产能的影响，且为正向影响，本文并不重点讨论，重点讨论启动压力梯度对产能的影响。

假设裂缝方向为x轴，对于低渗致密气藏，考虑启动压力梯度后，渗流公式可表示为：

$v=\frac{k}{{\mu }_g}\left(\frac{\partial p}{\partial y}-G\right)$ (1)

式中：G为启动压力梯度，10⁻¹ Mpa/cm；v为多孔介质中流体渗流速度，cm/s；p为孔隙压力，10⁻¹ Mpa；k为储层渗透率， ${10}^{-3}\mu {\text{m}}^2$ ； ${\mu }_g$ 为气体粘度，mPa·s；

低渗致密气藏由于自然产能较低，往往需要人工压裂，压裂后人工裂缝近井地带往往流速较高，一旦超过一定的雷诺数，流体本身惯性效应导致的附加压力损失不再可以忽略，需要考虑高速非达西效应，诸多学者从实验及理论两方面进行了深入研究 [10] [11] ，提出了很多非线性渗流表达式，其中以式(2)所展示的高速非达西渗流二项式模型应用最为广泛：

$\frac{\text{d}p}{\text{d}x}=\frac{\mu }{k}v+\beta {\rho }_g{v}^2$ (2)

式中： $\beta$ 为高速非达西渗流因子； ${\rho }_g$ 为气体密度，g/cm³；

稳定渗流时通过多孔介质各截面的质量流量不变，其渗流速度表达式为：

$v=\frac{q_m}{{\rho }_{g}A}=\frac{{\rho }_{gsc}{q}_{sc}}{{\rho }_g{w}_{f}h}$ (3)

式中： $q_{sc}$ 为流量，cm³/s； $w_f$ 为裂缝宽度，cm；h为储层厚度，cm；

在标准条件下天然气密度为

${\rho }_{gsc}=\frac{p_{sc}M}{R{T}_{sc}{Z}_{sc}}$ (4)

式中：Z为气体偏差因子；R为状态方程系数；

地层条件下，天然气密度为

${\rho }_g=\frac{pM}{RTZ}$ (5)

将式(4)、(5)代入到(3)中可得

$v=\frac{1}{w_{f}h}\frac{p_{sc}{q}_{sc}TZ}{T_{sc}{Z}_{sc}p}$ (6)

将式(6)代入式(2)得：

$\frac{\text{d}p}{\text{d}x}=\frac{\mu }{k_f{w}_{f}h}\frac{p_{sc}{q}_{sc}TZ}{T_{sc}{Z}_{sc}p}+\frac{\beta M}{w_f^2{h}^{2}TZp}{\left[\frac{p_{sc}{q}_{sc}TZ}{T_{sc}{Z}_{sc}}\right]}^2$ (7)

已有的研究表明，低渗致密气藏多孔介质一般存在比较明显的应力敏感性，不仅储层介质存在应力敏感性，人工裂缝同样存在应力敏感性，将人工裂缝考虑为变形介质可得

$k_f=k_{fi}{\text{e}}^{-{\alpha }_f\left(p_i-p\right)}$ (8)

式中： $k_f$ 为裂缝渗透率， ${10}^{-3}\mu {\text{m}}^2$ ； ${\alpha }_f$ 为裂缝介质变形系数；

式(7)代入(6)式中可得

$\frac{\text{d}p}{\text{d}x}=\frac{\mu }{k_{fi}{\text{e}}^{-{\alpha }_f\left(p_i-p\right)}{w}_{f}h}\frac{p_{sc}{q}_{sc}TZ}{T_{sc}{Z}_{sc}p}+\frac{\beta M}{w_f^2{h}^{2}TZp}{\left[\frac{p_{sc}{q}_{sc}TZ}{T_{sc}{Z}_{sc}}\right]}^2$ (9)

令

$b=\frac{{\text{e}}^{{\alpha }_f{p}_i}\mu }{k_{fi}{w}_{f}h}\frac{p_{sc}{q}_{sc}TZ}{T_{sc}{Z}_{sc}}$ ， $c=\frac{\beta M}{w_f^2{h}^{2}TZ}{\left[\frac{p_{sc}{q}_{sc}TZ}{T_{sc}{Z}_{sc}}\right]}^2$

式(9)可简化为

$\frac{p{\text{e}}^{{\alpha }_{f}p}}{b+c{\text{e}}^{{\alpha }_{f}p}}\text{d}p=\text{d}x$ (10)

对式(10)积分可得

$x=\frac{1}{{\alpha }_f^{2}c}\left[di\log \left(1+\frac{c}{b}{\text{e}}^{{\alpha }_{f}p}\right)-di\log \left(1+\frac{c}{b}{\text{e}}^{{\alpha }_f{p}_{wf}}\right)\right]+\frac{p}{{\alpha }_{f}c}\ln \frac{b+c{\text{e}}^{{\alpha }_{f}p}}{b+c{\text{e}}^{{\alpha }_f{p}_{wf}}}$ (11)

记裂缝端点处压力为 $p_f$ ，则

$x_f=\frac{1}{{\alpha }_f^{2}c}\left[di\log \left(1+\frac{c}{b}{\text{e}}^{{\alpha }_f{p}_f}\right)-di\log \left(1+\frac{c}{b}{\text{e}}^{{\alpha }_f{p}_{wf}}\right)\right]+\frac{p_f}{{\alpha }_{f}c}\ln \frac{b+c{\text{e}}^{{\alpha }_f{p}_f}}{b+c{\text{e}}^{{\alpha }_f{p}_{wf}}}$ (12)

式(12)建立的是 $q_{sc}$ 与 $p_{wf}$ 、 $p_f$ 关系。

式(1)、式(2)、式(8)分别给出了考虑启动压力梯度、裂缝中高速非达西效应以及裂缝应力敏感性的渗流方程，为分析致密气藏压裂井产能理论计算方法奠定了基础。

3. 压裂裂缝激发的椭圆渗流

低渗致密气藏压裂井生产时会在储层中激发平面二维椭圆渗流(假设储层等厚，形成的人工裂缝为垂直缝，且压开整段储层)，即形成以裂缝端点为焦点的共轭等压椭圆和双曲线流线族。分析前人关于扰动椭圆研究成果，引入发展的矩形族来描述等压椭圆族 [8] ：

$\bar{x}=x_{f}ch\left(\xi \right)$ (13)

$\bar{y}=\frac{2}{\text{π}}{\displaystyle {\int }_0^{\frac{\text{π}}{2}}b\sin \left(\eta \right)\text{d}\eta }=\frac{2x_f}{\text{π}}sh\left(\xi \right)$ (14)

式中，x,y为直角坐标； $\xi ,\eta$ 为椭圆坐标；

引入启动压力梯度后，式(1)在椭圆坐标中可以表示为：

$v=\frac{k}{{\mu }_g}\left(\frac{\partial p}{\partial \bar{y}}-G\right)$ (15)

质量渗流速度为：

${\rho }_v=\rho \frac{k}{{\mu }_g}\left(\frac{\partial p}{\partial \bar{y}}-G\right)=\frac{{\rho }_{sc}{q}_{sc}}{4x_{f}hch\left(\xi \right)}$ (16)

由式(14)可得：

$\frac{\text{d}p}{\text{d}\bar{y}}=\frac{\text{d}p}{\text{d}\xi }\frac{\text{d}\xi }{\text{d}\bar{y}}=\frac{\text{d}p}{\text{d}\xi }\frac{\text{π}}{2x_f}\frac{1}{ch\left(\xi \right)}$ (17)

由式(16)、式(17)可得：

$k\frac{p}{{\mu }_{g}Z}\left[\frac{\text{d}p}{\text{d}\xi }\frac{\text{π}}{2x_f}\frac{1}{ch\left(\xi \right)}-G\right]=\frac{p_{sc}T}{T_{sc}{Z}_{sc}}\frac{q_{sc}}{4x_{f}hch\left(\xi \right)}$ (18)

考虑储层介质的应力敏感性可得

$k{\text{e}}^{-{\alpha }_m\left(p_i-p\right)}\frac{p}{{\mu }_{g}Z}\left[\frac{\text{d}p}{\text{d}\xi }\frac{\text{π}}{2x_f}\frac{1}{ch\left(\xi \right)}-G\right]=\frac{p_{sc}T}{T_{sc}{Z}_{sc}}\frac{q_{sc}}{4x_{f}hch\left(\xi \right)}$ (19)

式中： ${\alpha }_m$ 为基质介质变形系数；

事实上储层介质的应力敏感性往往与启动压力梯度及滑脱效应耦合在一起。随着开发的进行，储层压力逐渐降低，储层介质孔隙度渗透率随之降低，同时启动压力梯度会逐渐增大，滑脱效应也会随之改变，耦合效应可通过应力敏感性、启动压力梯度综合等效表达，本文不做单独讨论。式(19)整理得：

$p{\text{e}}^{{\alpha }_{m}p}\left[\frac{\text{d}p}{\text{d}\xi }-2x_{f}ch\left(\xi \right)G/\text{π}\right]=\frac{p_{sc}{\text{e}}^{{\alpha }_{m}p}{\mu }_{g}ZT}{k{T}_{sc}{Z}_{sc}}\frac{q_{sc}}{2\text{π}}$ (20)

令：

$A=2x_{f}G/\text{π},B=\frac{p_{sc}{\text{e}}^{{\alpha }_{m}p}{\mu }_{g}ZT}{k{T}_{sc}{Z}_{sc}}\frac{q_{sc}}{2\text{π}}$

则微分方程(20)可变化为：

$p{\text{e}}^{{\alpha }_{m}p}\left[\frac{\text{d}p}{\text{d}\xi }-Ach\left(\xi \right)\right]=B$ (21)

边界条件为

${\xi }_e=\ln \frac{2r_e}{x_f},p=p_e$

式(21)给出的非线性常微分方程精确解求解十分复杂，略去高阶小量，得到式(21)方程的近似解析解为：

$\begin{array}{l}A\frac{x_f}{r_e}-AB\frac{x_f}{r_e}\frac{1+{\alpha }_m{p}_e}{p_e^2{\text{e}}^{\alpha p_e}}-AB\frac{x_f}{r_e}\frac{2+{\alpha }_m^2{p}_e^2}{p_e^5{\text{e}}^{{\alpha }_m{p}_e}}\left(\frac{B}{p_e{\text{e}}^{{\alpha }_m{p}_e}}+A\frac{x_f}{r_e}\right)+(-B^2\frac{1+{\alpha }_m{p}_e}{p_e^3{\text{e}}^{2{\alpha }_m{p}_e}}\\ -AB\frac{x_f}{r_e}\frac{1+{\alpha }_m{p}_e}{p_e^2{\text{e}}^{{\alpha }_m{p}_e}}+A\frac{x_f}{r_e})\left[B^2\frac{2{\alpha }_m^2{p}_e+4{\alpha }_m+3}{p_e^3{\text{e}}^{2{\alpha }_m{p}_e}}+AB\frac{x_f}{r_e}\left({\alpha }_m^2{p}_e^2+2{\alpha }_m{p}_e+2\right)\right]\\ +\left(\frac{B}{p_e{\text{e}}^{{\alpha }_m{p}_e}}+A\frac{x_f}{r_e}\right)\left[AB\frac{x_f}{r_e}\left({\alpha }_m^2{p}_e^2+2{\alpha }_m{p}_e+2\right)-\frac{4{\alpha }_m^3{p}_e^2+\left(12{\alpha }_m^2+6{\alpha }_m\right)p_e+12{\alpha }_m+9}{p_e^4{\text{e}}^{2{\alpha }_m{p}_e}}\right]\\ +AB\frac{x_f}{r_e}\left(2{\alpha }_m^2{p}_e+2{\alpha }_m\right){\left(\frac{B}{p_e{\text{e}}^{{\alpha }_m{p}_e}}+A\frac{x_f}{r_e}\right)}^2-\left(-B^2\frac{1+{\alpha }_m{p}_u}{p_u^3{\text{e}}^{2{\alpha }_{m}p}}-AB\frac{1+{\alpha }_m{p}_u}{p_u^2{\text{e}}^{{\alpha }_m{p}_u}}\right)\end{array}$

$\begin{array}{l}\times \left[B^2\frac{2{\alpha }_m^2{p}_u+4{\alpha }_m+3}{p_u^3{\text{e}}^{2{\alpha }_m{p}_u}}+AB\left({\alpha }_m^2{p}_u^2+2{\alpha }_m{p}_u+2\right)\right]\\ -\left(\frac{B}{p_u{\text{e}}^{{\alpha }_m{p}_u}}\right)\left[-\frac{4{\alpha }_m^3{p}_u^2+\left(12{\alpha }_m^2+6{\alpha }_m\right)p_u+12{\alpha }_m+9}{p_u^4{\text{e}}^{2{\alpha }_m{p}_u}}\right]\\ +AB\frac{1+{\alpha }_m{p}_u}{p_u^2{\text{e}}^{{\alpha }_m{p}_u}}-AB\left(2{\alpha }^2{p}_u+2{\alpha }_m\right){\left(\frac{B}{p_e{\text{e}}^{{\alpha }_m{p}_u}}+A\right)}^2=0\end{array}$ (22)

式中： $p_u$ 裂缝中平均压力，10⁻¹ Mpa；

式(22)建立的是 $q_{sc}$ 与 $p_u$ 的关系，因人工裂缝激发的椭圆流与人工裂缝中的流动在交界面出压力相等，将式(22)与式(12)联立可求得产量与井底流压之间的函数关系。

4. 低渗致密气藏压裂井实例计算

以X低渗致密气藏实际参数为基础，研究不同因素对压裂井产能的影响规律。X低渗致密气藏原始地层压力为30 MPa，温度为106℃，渗透率为3 × 10⁻³ μm，供给边界为300 m，有效厚度为10 m，压裂裂缝半长为100 m，裂缝宽度为2 mm，裂缝中渗透率为250 μm²，气体粘度为0.02 mPa·s。

从图1可以看出，拟启动压力梯度对低渗透产能的影响较为明显，启动压力梯度越大，产能越低，且井底流压越高，即生产压差越小，动用范围越小，产能降低越快。

从图2可以看出，低渗致密气藏基质变形介质系数越大，初期产能越低，由于介质变形系数越大，同样生产条件下，渗流阻力越大，渗透率下降幅度越大。裂缝介质变形系数对产能影响规律与基质变形系数影响规律一致，此处不再赘述。

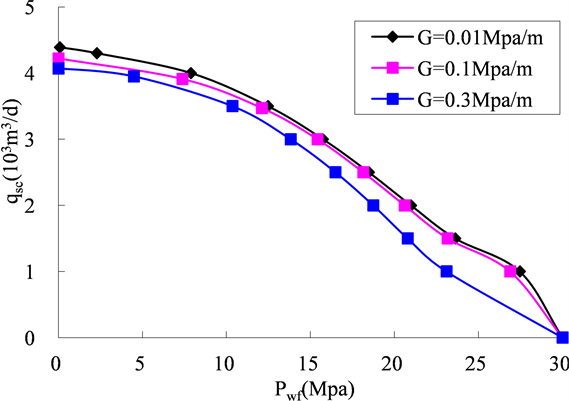
Figure 1. Influence law of threshold pressure gradient on productivity change in low permeability tight gas reservoir

图1. 拟启动压力梯度对低渗致密气藏产能影响规律

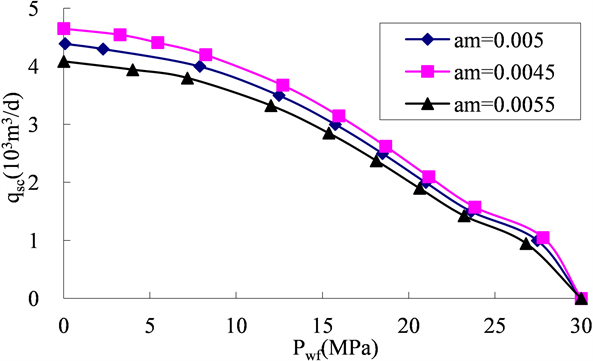
Figure 2. Influence law of deformed media on productivity change in low permeability tight gas reservoir

图2. 变形介质系数对低渗致密气藏产能影响规律

由图3可以看出，高速非达西渗流系数越大，同样情况下裂缝中渗流阻力越大，产能越低。同时，随着井底流压升高，曲线存在不平滑拐点，其主要原因为生产压差变小后，高速非达西效应减小甚至消失，导致产能曲线上有上凸之处。

由图4、图5可以看出，裂缝半长越长、裂缝导流能力越大，产能越高；只是两者影响机理不尽相同。裂缝半长越长，激发的椭圆流长轴越长，裂缝导流能力越长，椭圆流短轴越长。

5. 结论

1) 基于扰动椭圆及发展的矩形族思想，给出了同时考虑启动压力梯度、裂缝近井地带高速非达西效应、气藏基质及裂缝应力敏感性等因素影响的压裂井产能计算方法，并给出了解析解。

2) 拟启动压力梯度、高速非达西渗流系数、压裂变形介质系数、裂缝长度以及裂缝导流能力均对产能有影响。保持井底压力不变前提下，拟启动压力梯度、高速非达西渗流系数、介质变形系数越小，压裂气井产能越大；裂缝长度越长、裂缝导流能力越大，压裂气井产能越大。同时，随着井底流压升高，

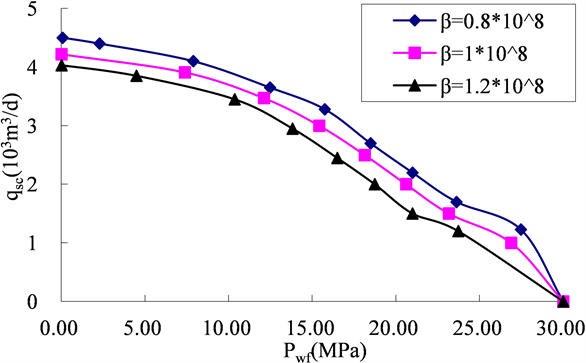
Figure 3. Influence law of high speed non-Darcy flow coefficient on productivity change in low permeability tight gas reservoir

图3. 高速非达西渗流系数对低渗致密气藏产能影响规律

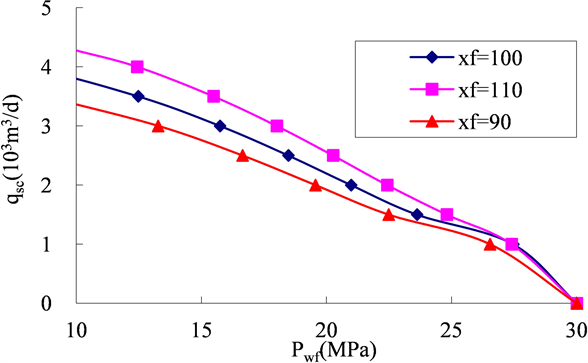
Figure 4. Influence law of fracture length on productivity change in low permeability tight gas reservoir

图4. 裂缝半长对低渗致密气藏产能影响规律

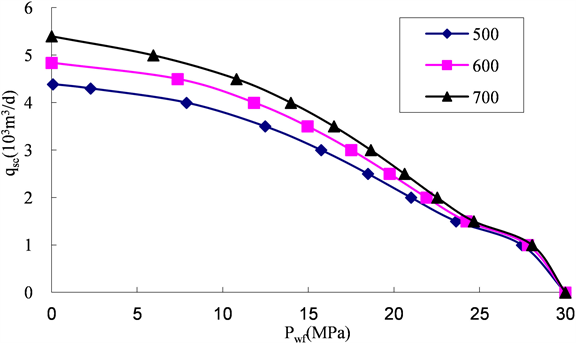
Figure 5. Influence law of fracture conductivity on productivity change in low permeability tight gas reservoir

图5. 裂缝导流能力对低渗致密气藏产能影响规律

曲线存在不平滑拐点，其主要原因为生产压差变小后，高速非达西效应减小甚至消失，导致产能曲线上有上凸之处；井底流压继续降低、生产压差进一步减小后，由于启动压力梯度存在导致整个储层动用范围变小，产能加速下降直至降为0。

3) 对于低渗致密气藏，在对压裂气井进行配产设计时一定要考虑拟启动压力梯度、高速非达西效应以及介质变形系数对产能的影响，同时在压裂设计时要优化裂缝的长度及导流能力。

基金项目

十三五国家重大科技专项项目——超深井碳酸盐岩储层改造及测试关键技术(编号：2017ZX05005-005)。