1. 引言
在期货市场,贵金属具有保值、增值、抵抗通胀的金融功效。近年来随着我国贵金属市场交易规模逐年扩大,对贵金属期货价格的运行特征进行比较系统的研究日益受到金融业界的重视。从技术层面上看,由于受到我国期货市场观测数据量的限制,试图利用诸如Copula等常规统计方法研究80多个期货价格精确的联合概率分布函数及其相应的投资组合问题其难度是相当大的。另一方面,任何金融投资机构由于受到有限资金量等客观因素的限制,不可能在同一时间对所有的期货产品进行投资。投资机构更倾向于选出若干个风险较小且有更多获利机会的期货产品进行投资。
关于贵金属相关的期货产品,国内较少能够找到以其相关的时间序列分析研究。基于此,本文总结了我国贵金属期货价格对数收益率序列(lrt)的基本统计特征,建立了相应的ARMA-GARCH模型、EGARCH模型并进行了风险值计算。基于这些统计指标,建议了一种如何从市场上交易的贵金属期货产品中优选出最有可能盈利且风险较小的期货产品池的策略。这一预选出的期货产品池由于其投资品种数目少,有利于今后的期货交易投资组合策略的研究。
2. 贵金属合约数据的基本统计特征
本文考察2011.1~2016.12期间的贵金属产品,由于期货合约交易时间普遍较短,不具有充分的日交易数据进行时间序列分析,故在此选择交易日期数超过200天的期货品种(即针对每年年底交割的期货合约),总计83个合约,对每个期货合约的对数收益率序列进行诸如平均值、中位数、偏度值、峰度值、Jarque-Bera正态性检验以及自相关性等统计指标的数据分析。
图1将每个产品的对数收益率按照其偏度值(skewness)和峰度值(kurtosis)作图,x轴代表偏度值,y轴代表峰度值(即是否尖峰,备注:此处的峰值是指超额峰值,即超过正态分布峰值的值——峰值减去3)。可以明显观察到,所有的贵金属期货产品的峰度值均为正值。通过聚类分析,数据散点图被一个明显的双翼型曲线分成三个部分,铷、钌等贵金属处于双翼型上边的中央部分,偏度值集中在(−0.25, 0),峰度值在(1, 3)之间。图中双翼型曲线的左翼区域集中了2011~2014年的品种,包括锌、银、金、线材等,右翼区域集中包括锌、银、铜等品种,大多属于2015~2016年间的合约。
从图1可以看到2015~2016年的品种的偏度大多为正值,2011~2014年的品种的偏度大多为负值,这一结果可能与市场行情相关。2015~2016年商品市场偏牛市行情,故偏度大多为正值;2011~2014年商品市场偏熊市行情,故偏度大多为负值。而位于双翼型上边的铷、钌等期货品种在2015年前后的偏度特征与市场的牛熊并无明显的关联。
目前市场上较受欢迎的投资原则是在风险程度较小的水平上获得更高的收益率。在牛市中,可以考虑图1中右翼区域低峰度右偏的期货品种做多。偏度右偏代表预期有更多可能获得一个较高的平均收益水平,低峰度代表波动率位于一个较大的范围内,对于偏重于实施低买高卖差价交易的投资机构,相对容易获取更高的价差操作收益。同理,熊市中可以考虑图1中左翼区域低峰度左偏的期货品种做空。
3. ARMA-GARCH建模
3.1. 示例分析
限于篇幅,本文从83个期货合约中选取沪锌1612 (zn1612)和沪铝1401 (al1401)这两个有代表性的期货品种的建模结果进行详述。本文所采用的建模方法可以参考文献 [1] 和 [2] ,相应的Eviews操作可以参考文献 [3] 。
3.1.1. 沪锌1612 (zn1612)
由对数收益率的直方图和经验分布曲线图(图2)可得对数收益率整体分布与正态分布有明显差距,且有十分显著的尖峰效应,主要集中在(−0.02, 0.02)区域中;从图3的Q-Q图中可以得到同样的结果。进一步进行Box-Ljung检验,p值为0.0007341,可知对数收益率有明显的自相关性。
由图4的ACF图可得滞后水平为3、15、20的自相关度在5%水平下显著,故进行ARMA模型拟合和ARCH检验。再对通过ARMA模型剩下的残差进行是否具有GARCH效应的检验并对其建立GARCH模型,数据的一部分自相关性由GARCH模型反应,故ARMA模型的拟合结果出现降阶情况。ARMA模型对应的估计值方差为0.000207,对数似然函数值为653.5,AIC值为−1299,AICc值为−1298.83,BIC值为−1285.23。
最后拟合了均值为0.002269384的ARMA (1,1) + GARCH (1,1)模型,t时刻对数收益率rt所拟合的方程为
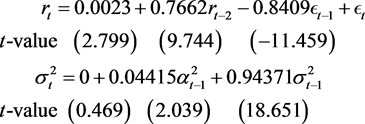

Figure 2. Histogram and experience distribution curve of logarithmic rate of return
图2. 对数收益率的直方图和经验分布曲线图
3.1.2. 沪铝1401 (Al1401)
与沪锌1612的分析过程相同,图5为沪铝1401对数收益率的直方图和经验分布曲线图,图6为Q-Q图,图7为ACF图。最后拟合了平均值为−0.0005671886的ARMA (0,1) + GARCH (0,1)模型,其相应的方程为,
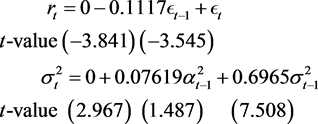

Figure 5. Histogram and experience distribution curve of logarithmic rate of return
图5. 对数收益率的直方图和经验分布曲线图
其中ARMA模型中对应的估计值方差为0.00002138,对数似然函数值为903.33,AIC值为−1800.66,AICc值为−1800.55,BIC值为−1790.37。
3.2. 结果分析
同3.1中两个示例,其他81个合约结果的建模结果与其相似。总体来说,所有的样本都呈现了明显的尖峰性,平均数均在0附近,基本可以视为0,且具有明显的自相关性,可以通过ARMA模型来拟合,其残差有较为明显的ARCH效应,可进行GARCH建模。
4. EGARCH模型
金融产品波动率对正的资产收益率和负的资产收益率的反应具有非对称效应,限于篇幅,本文依据文献 [2] 的方法并仅以沪锌1612和沪铝1401为例考察它们的EGARCH建模结果。
4.1. 沪锌1612
对沪锌1612所建的EGARCH模型为
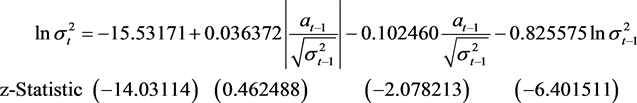
C(3) = −0.102460在5%水平下显著,该股票杠杆效应不明显。当at−1 < 0时,它给条件方差的对数带来的冲击大小为0.138832倍;当at−1 > 0时,它给条件方差的对数带来的冲击大小为−0.066088倍。图8左子图所示的信息冲击曲线可直观看出沪锌1612对利空和利多消息的反应不对称,利空消息产生的波动稍大于利多消息,但都很微弱。
4.2. 沪铝1401
对沪铝1401所建立的EGARCH模型为
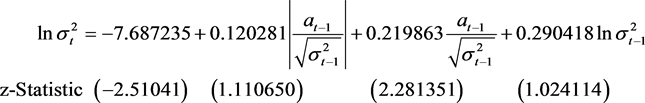
C(3) = 0.219863在5%水平下显著,该股票杠杆效应不明显。当at−1 < 0时,它给条件方差的对数带来的冲击大小为0.011924倍;当at−1 > 0时,它给条件方差的对数带来的冲击大小为0.204672倍。如图8右子图所示的信息冲击曲线可直观看出沪铝1401对利空和利多消息的反应不对称,利多消息产生的波动稍大于利空消息,但都很微弱。
4.3. 结论
同上述两个示例,其他81个合约结果的建模结果与其相似。总体来说,所有的样本对正的资产收益率和负的资产收益率有非对称效应,且波动都很微弱。
5. 风险值(VAR)
根据文献 [1] ,5%风险值的计算公式为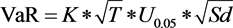 ,其中K表示资金数量,U0.05表示
,其中K表示资金数量,U0.05表示
基于本文所建ARMA-GARCH模型进行模拟所获得的下5%分位数,Sd表示样本方差。以单一期货品种沪锌1612为例,预估一年的交易天数为220,该品种的对数收益率并非正态分布,故由模拟出的Q-Q图9可得最左侧5%的分位数的模拟均值为1.75σ,样本方差为0.000207。投资者持有一百万元该期货的1年期合约的5%VAR为373,452元。
对83个期货产品按照图1的偏度—峰度图左中右三部分分类,分别做Box图10,可以看出图1中右翼期货品种(偏度值为正)的VaR分布较其他两类更为集中,且VaR的中位数低于其他两类。故图1中牛市右翼区域的期货品种风险值比熊市左翼区域品种的风险值普遍偏低,机翼上部区域期货品种的风险值中位数高于左右机翼两个部分。这从一个侧面支持了从图1机翼型右边区域选择做多期货池及左边区域选择做空期货池的观点。
6. 结论
本文从数据的基本统计特征、ARMA-GARCH模型、EGARCH模型、风险值四个部分对贵金属相关的期货品种在2011~2016年间的对数收益率进行了分析,建议了一种在牛市和熊市选取以贵金属为标的的期货品种池的策略,以供业界参考。
致谢
本文作者感谢本项目课题组指导老师林建忠副教授的悉心指导。此外,还要感谢何欣和王天宇两同学给予的建议和帮助。
基金项目
本项目受第十四期上海交通大学大学生创新实践计划和2017年上海市大学生创新活动计划资助。