二级直齿轮空间驱动机构传动误差分析

Analysis of Transmission Error of Two-Stage Spur Gear Space Driving Mechanism

摘要: 为提高某型号空间驱动机构两级直齿轮系统的传动精度，解决系统运行过程中的非线性扰振问题，以简谐函数的形式来描述齿形误差和齿距误差，分析了齿形误差和齿距误差对齿轮系统整体传动误差的影响。分析结果表明，第二级齿轮的齿形齿距误差对传动误差影响较大，而且相比于齿轮3，齿轮4的影响更大；相比于齿形误差，齿距误差的影响更大。本文丰富了二级直齿轮系统传动误差方面的研究，为实际设计齿轮系统提供重要参考依据。

Abstract: To improve the transmission accuracy of the two-stage spur gear system of a certain type of space drive mechanism, solving the nonlinear disturbance problem in the operation of system operation, the profile error and the pitch error was described by simple harmonic function and the influence of profile error and pitch error on the overall transmission error of gear system was analyzed. The results show that the pitch error of the second stage gear pair has a great influence on the transmission error, and the gear 4 has a greater effect than the gear 3, and the influence of the pitch error is greater than that of the profile error. This paper enriches the research on the transmission error of the two-stage spur gear system, and provides an important reference for the actual design of the gear system.

1. 引言

齿轮系统广泛应用于机床、汽车、航空航天、船舶和风力发电等领域。传动精度是评价传动系统的一个重要技术指标。近年来，许多高校和研究机构对齿轮传动系统做了大量研究 [1] [2] [3] [4] 。系统运行过程中的振动和噪声主要是由内部激励和外部激励引起，内部激励作为一个重要因素，其很大程度上取决于齿轮的轮廓设计、加工方法和装配误差。因此，对这些激励因素进行分析具有十分重要的研究意义 [5] [6] [7] [8] 。

传动误差会降低机器工作的可靠性与精度，甚至严重时导致齿轮或其他零件的损坏，从而使传动系统失效而导致严重后果 [9] 。齿轮减速系统的传动误差主要是由齿型误差和齿距误差产生。国内外对传动误差进行了大量研究，但在齿距误差方面的研究相对较少 [10] [11] [12] 。西班牙学者Fernández等 [13] 在分析齿轮系统时考虑了齿型误差和齿廓修型的影响，并分别进行了准静态分析和动态分析，但是并未考虑齿距误差的影响。北京工业大学的石照耀教授 [14] 针对传动误差在研究中存在的一些局限性，提出了齿轮副整体误差的概念，并给出了测量实例。重庆理工大学的程晓伟 [15] 齿轮副传动误差的理论计算模型，探讨了二级直齿轮传动误差的计算方法，并对实验数据和理论计算数据进行对比，经过修正的到了更合理的二级齿轮传动误差计算模型。

本文的研究对象是某型号二级直齿轮空间驱动机构，针对该机构在运行过程中产生的非线性扰振问题，提出了齿型误差和齿距误差的计算公式，进而求得齿轮系统的整体传动误差。通过改变齿型误差和齿距误差参数，仿真不同加工条件下整体传动误差的变化，进而找出引起非线性扰振的影响因素。本文丰富了二级直齿轮系统传动误差方面的研究，为实际设计齿轮系统提供重要参考依据。

2. 两级直齿轮传动模型

空间驱动机构的结构较为复杂，而本文以提高系统的传动精度、降低扰振为目的，因此应重点考虑齿轮减速系统的影响，并做出以下假设：

1) 忽略轴承的摩擦；

2) 认为齿轮减速系统的输入扭矩为固定值：

3) 轮齿始终沿啮合线方向进行啮合。

对间驱动机构二级直齿轮减速系统进行简化，简化后的传动模型如图1所示，其动力传输过程如图中箭头所示。

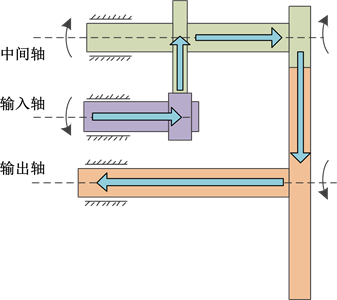
Figure 1. Transmission diagram of two-stage spur gear

图1. 二级直齿轮传动示意图

两级齿轮传动系统的齿轮参数如表1所示。

3. 齿型误差和齿距误差

这里采用简谐函数来表示该误差，将齿形和齿距这两种误差分别表示为一种三次谐波函数，如下式：

$e_{pf}=a_1\sin \left(\alpha \right)+b_1\sin \left(2\alpha \right)+c_1\sin \left(3\alpha \right)$ (1)

$e_{pt}=a_2\sin \left(\theta \right)+b_2\sin \left(2\theta \right)+c_2\sin \left(3\theta \right)$ (2)

式中

$e_{pf},e_{pt}$ ——齿形误差和齿距误差；

$a_1,b_1,c_1$ ——齿形误差各阶谐波的幅值系数；

$a_2,b_2,c_2$ ——齿距误差各阶谐波的幅值系数；

$\alpha$ ——啮合角；

$\theta$ ——齿轮转角。

综上，齿轮传动误差表示为

$e_t=e_{pf}+e_{pt}$ (3)

通过Matlab编程得到四个齿轮的齿型和齿距误差曲线，如图2和图3所示。

4. 齿形齿距误差对传动误差的影响

4.1. 第一级与第二级齿轮副的对比

为了研究齿形齿距误差对齿轮减速系统传动误差的影响，分别对齿轮系统四个齿轮的齿形齿距误差进行修改，修改为默认值的80%和120%，用于模拟齿轮加工精度的提高或降低带来的齿形和齿距误差。修改后的具体组合如表2所示，然后对传动误差进行求解，求解结果如图4所示。从图4中可以看出，不同齿形齿距误差组合下的传动误差变化趋势相同，但是波动幅度不同。为了对比明显，将传动误差最大值处进行局部放大，并将各种组合分别与组合1进行对比，得到8组对比曲线，如图5所示。

通过对比不同齿型齿距误差组合下的传动误差曲线可知，仅改变第一级齿轮的齿形齿距误差对齿轮系统的传动误差影响较小，如图5中(a)和(b)所示；改变第二级齿轮的齿形齿距误差对齿轮系统的传动误差影响较大，如图5中(c)~(h)所示。为了更直观地分析齿形齿距误差对齿轮系统的影响，提取各传动误差曲线的幅值，并计算各齿形齿距误差下的传动误差幅值变化量，汇总后如表3所示。

Figure 2. Curve of profile error

图2. 齿形误差曲线

Figure 3. Curve of pitch error

图3. 齿距误差曲线

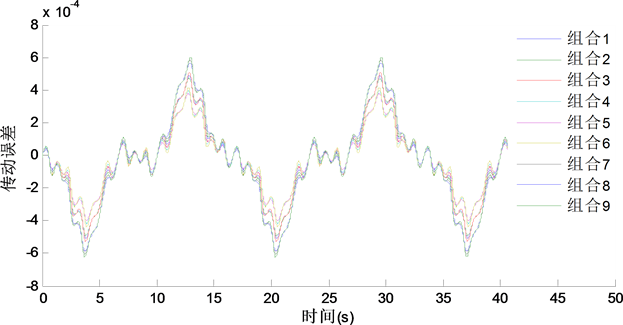
Figure 4. Transmission error curve under different profile error and pitch error combination

图4. 不同齿形齿距误差组合下的传动误差曲线

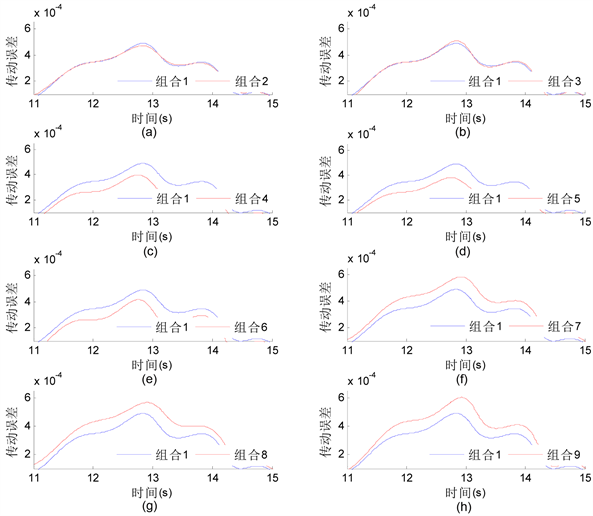
Figure 5. Comparison of different error combination and default combination (1)

图5. 不同齿形齿距误差组合与默认组合的传动误差对比图(1)

Table 1. Basic parameters of two-stage spur gear

表1. 二级齿轮系统的基本参数

Table 2. Different profile error and pitch error combination (1)

表2. 不同齿形误差和齿距误差组合(1)

Table 3. Transmission error amplitude under different combinations (1)

表3. 不同组合下的传动误差幅值汇总(1)

从表3中可以很明显的看出，增大第一级齿轮或第二级齿轮的齿形齿距误差会使齿轮系统的传动误差增大，如表3中组合3、组合7和组合9所示；减小第一级齿轮或第二级齿轮的齿形齿距误差会使齿轮系统的传动误差减小，如表3中组合2、组合4和组合5所示。

组合2和组合3仅改变了第一级齿轮的齿形齿距误差，其传动误差幅值变化量百分比在−4%~4%之间，组合4和组合7仅改变了第二级齿轮的齿形齿距误差，其传动误差幅值变化量百分比在−20%~20%之间，可见仅改变第一级齿轮的齿形齿距误差对齿轮系统的传动误差影响较小，改变第二级齿轮的齿形齿距误差对齿轮系统的传动误差影响较大。

4.2. 第二级齿轮中齿轮3与齿轮4的对比

针对第二级齿轮影响较大之一特点，保证第一级齿轮的齿形齿距误差不变，仅改变齿轮3和齿轮4的齿形齿距误差，进一步进行仿真分析，修改后的齿形齿距误差如表4所示，局部放大后的传动误差曲线对比如图6所示，汇总表如表5所示。

从表5中可以很明显的看出，增大齿轮3或齿轮4的齿形齿距误差会使齿轮系统的传动误差增大，如表4中组合11、组合15和组合17所示；减小齿轮3或齿轮4的齿形齿距误差会使齿轮系统的传动误差减小，如表4中组合10、组合12和组合13所示。

组合10和组合11仅改变了齿轮3的齿形齿距误差，其传动误差幅值变化量百分比在−5%~5%之间，组合12和组合15仅改变了齿轮4的齿形齿距误差，其传动误差幅值变化量百分比在−16%~16%之间，可见仅改变齿轮3的齿形齿距误差对齿轮系统的传动误差影响较小，改变齿轮4的齿形齿距误差对齿轮系统的传动误差影响较大。

4.3. 第二级齿轮中齿形误差与齿距误差的对比

针对第二级齿轮影响较大之一特点，保证第一级齿轮的齿形齿距误差不变，分别改变第二级齿轮的齿型误差和齿距误差，进一步进行仿真分析，修改后的齿形齿距误差如表6所示，局部放大后的传动误差曲线对比如图7所示，汇总表如表7所示。

从表7中可以很明显的看出，增大第二级齿轮的齿型误差或齿距误差会使齿轮系统的传动误差增大，如表7中组合19、组合23和组合25所示；减小第二级齿轮的齿型误差或齿距误差会使齿轮系统的传动误差减小，如表7中组合18、组合20和组合21所示。

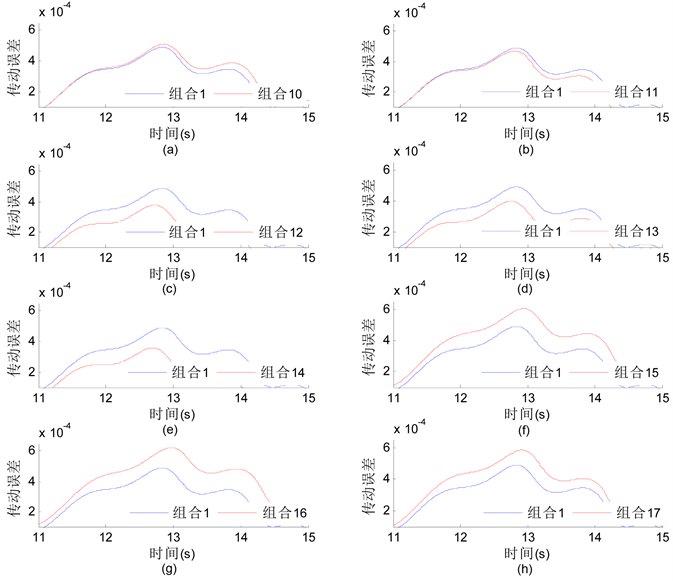
Figure 6. Comparison of different error combination and default combination (2)

图6. 不同齿形齿距误差组合与默认组合的传动误差对比图(2)

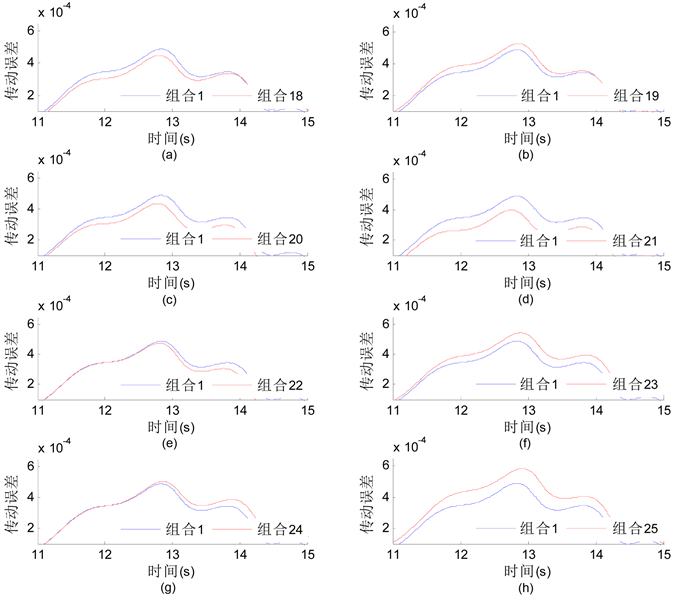
Figure 7. Comparison of different error combination and default combination (3)

图7. 不同齿形齿距误差组合与默认组合的传动误差对比图(3)

Table 4. Different profile error and pitch error combination (2)

表4. 不同齿形误差和齿距误差组合(2)

Table 5. Transmission error amplitude under different combinations (2)

表5. 不同组合下的传动误差幅值汇总(2)

Table 6. Different profile error and pitch error combination (3)

表6. 不同齿形误差和齿距误差组合(3)

Table 7. Transmission error amplitude under different combinations (3)

表7. 不同组合下的传动误差幅值汇总(3)

组合18和组合19仅改变了第二级齿轮的齿形误差，其传动误差幅值变化量百分比在−9%~9%之间，组合20和组合23仅改变了第二级齿轮的齿距误差，其传动误差幅值变化量百分比在−12%~12%之间，可见相比之下，改变齿距误差较改变齿形误差对齿轮系统的传动误差影响大。

5. 结论

1) 分析了齿形齿距误差对齿轮系统传动误差的影响，分析结果表明，第二级齿轮的齿形齿距误差对传动误差影响较大，而且相比于齿轮3，齿轮4的影响更大，相比于齿形误差，齿距误差的影响更大。

2) 在实际设计二级直齿轮传动系统时，为了提高传动精度，应优先提高第二级齿轮的精度等级。在齿轮的制造和加工过程中，应将齿轮4的齿形齿距误差控制在一定范围内，尤其是齿距误差。在保证传动精度的前提下，为了降低成本，可适当降低第一级齿轮的精度等级，对齿轮系统的传动误差影响较小。

3) 本文丰富了二级直齿轮系统传动误差方面的研究，为实际设计齿轮系统提供重要参考依据。

基金项目

北京市教委项目(JC001011201601)。