1. 引言
牛顿“万有引力定律”(1687年)是17世纪自然科学的伟大成果, 它把地面上物体运动和天体运动的规律统一了起来。牛顿之后三百多年,科学家始终没有测量出作为基本物理常数的引力相互作用传播速度(简称引力速度)。
在引力和电磁这两种长程相互作用中,人们对电磁相互作用规律的了解更深一些。在麦克斯韦电磁理论中,光速
。即光速与电磁理论中的真空介电常数和真空磁导率常数之间有简单的关系。所以,光速(电磁波速)的确定,对电磁学理论的建立,有重要作用。引力速度测定,对引力相互作用理论的完善是十分必要的。
引力速度没有测定,加之牛顿“万有引力定律”中不显含时间,不少人认为引力可以瞬间传播。而狭义相对论指出,光速是所有物理作用速度上限 [1] 。另一些科学家则认为引力作用以光速传播。基本物理常数认识上存在着严重分歧。
对大自然基本常数之一的物体间引力作用传播速度测量无疑是一个亟待解决的重大科学问题。但引力作用极其微弱且无法屏蔽、传播速度又快,依靠现有技术在实验室中测量引力速度没有可能。
罗默(Ole Christensen Roemer)利用木卫食现象首次测出光速。引力速度是否也能利用太阳系中行星、卫星在引力相互作用下的运动效应测量?——如果在运动天体上有能够观测到另一天体对其引力变化的仪器,且有足够高的时间分辨率,引力速度就有测出的可能。
地球物理学为探索地球内部结构和探矿研制出的高精度重力仪,在地球平台上已经能够清晰记录到日月引力的变化,且具有足够高的时间分辨率。
中国科学院地质与地球物理研究所汤克云团队从中国地震局西藏狮泉河站和新疆乌什站PET型弹簧重力仪固体潮观测数据,比较固体潮理论值、引力瞬间传播理论值与观测值相同相位的时间滞后,用时间域资料得出引力以光速传播,相对误差5%的结论 [2] [3] 。
如果汤克云这项工作的结论正确,就是中国科学家在国际上首次测得引力速度,无疑是物理学的一个基础性重要结果。
对汤克云团队的研究结论,有支持的、也有反对和怀疑的或不能判断真伪的。为对这项工作的科学性达成共识,中科院组织了两次评议研讨会,有9位院士、11位研究员参会。会上支持和反对的院士都有。比较一致的看法是,问题最终在天体位置(视位置与真位置)的确定。研讨会未能达成共识,反对意见较多,但也不能证明汤的这项工作就是错的。
在维基百科的Gravity词条下,关于Speed of gravity一段,目前只介绍了两项关于测量引力速度的工作:“2012年12月,中国的一个研究团队宣布,他们已经测量了地球潮汐的相位滞后时间,这似乎证明了引力的速度等于光速;……在2017年10月,LIGO和室女座探测器在伽玛射线卫星和光学望远镜两秒钟内接收到来自同一方向的引力波信号。这证实了引力波的速度与光速相同” [4] 。
被推选为2003年度世界十大科技进展候选项目,由理论物理学家Kopeikin和射电天文学家Fomalont利用木星掩食射电类星体机会,用射电望远镜阵观测类星体位置变化,宣称首次测得引力以光速传播的结果(误差20%) [5] ,却没有列入维基百科该词条。这说明,中国科学家用测量地球潮汐相位滞后时间测量引力速度的科学思路,在国际上并未被否定。
本文从重力固体潮理论、计算、天体位置如何确定等方面加以述说,如何从台站固体潮观测值与理论值的符合,得出引力相互作用的传播速度与光速相同。
汤克云用乌什和狮泉河站弹簧重力仪一天的观测数据,在时间域中分析得出引力以光速传播的结论。本文根据中国科学院测量与地球物理研究所武汉站观测精度更高的超导重力仪3年连续观测数据,用调和分析方法分离出月亮M2波和太阳S2波,根据它们各自的观测值相对于理论值的相位差均接近于零,在频率域中分析再次得到引力以光速传播的结论。
本文还从日月位置须作光行差校正这一天文常规操作,从逻辑上指出:引力速度只能与光速相同。
下面先简单介绍日月引力引起地球重力固体潮的计算表达。
2. 重力固体潮理论值的计算表达
重力固体潮由日月引力变化造成,测站的重力固体潮理论值由牛顿万有引力定律计算。
万有引力定律表示为如下公式
(1)
以月球和地球为例,m为月球质量,M为地球质量,rm为月心与地心之间的距离,F为月球与地球的相互引力,G为引力常数。如图1所示。
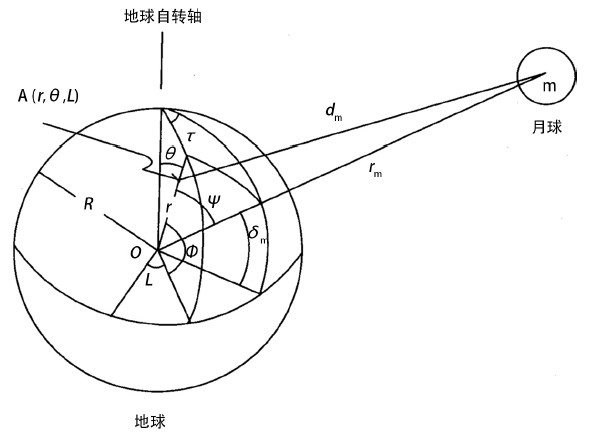
Figure 1. Earth and moon coordinate position diagram. τ, δm, Ψ, rm, m, dm are the moon’s hour angle, declination, the polar angle of the moon, the distance from the moon’s heart to the center of the earth, the mass of the moon, and the distance from the moon’s heart to the point A. τs, δs, Ψs, rs, ms, ds are , respectively, The solar hour angle, declination, solar polar angle, the distance from the heliocentric to the geocentric, the mass of the sun, and the distance from the heliocentric to point A
图1. 地球与月球坐标位置示意图。τ,δm,Ψ,rm,m,dm分别为月球时角、赤纬、月球极角、月心到地心距离、月球的质量、月心到A点的距离;当图1中月球改为太阳时,上述参数用τs,δs,Ψs,rs,ms,ds表示
点的月球引力位
为 [6] [7] :
(2)
勒让德多项式
是A点的纬度
和天体在观测时刻的赤纬
、时角
和极角
的函数。
A点的引潮力位
等于天体对地球上单位质点的引力位
加上公转时单位质点的惯性离心力位
:
(3)
重力潮汐
是引潮力位在垂直方向的导数:
(4)
在观测点A记录到的重力固体潮是观测时刻日月的质量、时角、赤纬、极角、到地心距离、到A点距离的函数。
计算地球某测站A于某时间段的重力固体潮理论值,只须在计算程序中输入测站的经纬度、高程和所计算时间段的起始和终止时刻。
图2是新疆乌什站PET重力仪2009年7月21~22日的重力观测值经低通滤波滤去地脉动噪声后的
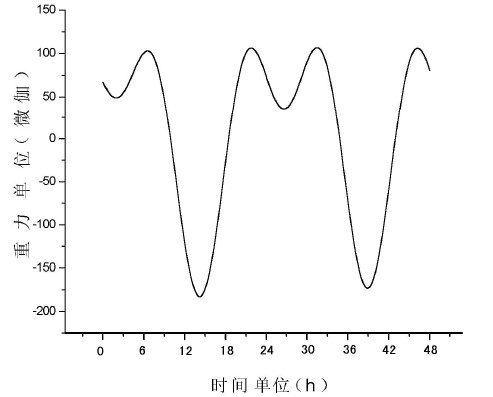
Figure 2. Observations of gravity earth tide recorded on July 21-22, 2009 recorded by PET gravimeter of Wushi station, Xinjiang
图2. 新疆乌什站PET型重力仪记录的2009年7月21~22日的重力固体潮观测值
重力固体潮。重力潮幅约280 μgal (微伽),只有地球表面重力值的三百五十万分之一。
理论值(乘以潮汐因子值)与观测值之间的差别很小,两条曲线几乎重叠在一起,经多次局部放大才看出差别。
用重力固体潮观测确定引力速度,测站测到的重力固体潮与日月引力之间是什么关系?
3. 重力固体潮与日月引力的关系
按定义,测站A的重力固体潮是日月对A点的引潮力在垂直方向的分量。日月对A点的引潮力则是日月对A点引力与对地心引力之矢量差。
重力固体潮与日月引力之间是什么关系?下面以太阳为例,先看太阳对A点的引潮力和太阳引力的关系。
设想地球绕太阳轨道的偏心率为零,太阳对地球质心的引力就是常量。太阳到测站A的距离dm因为地球自转而变化,A受到的引力出现周期性变化。地球上单位质量受到太阳引力约0.6 gal (伽),太阳对A点的引潮力幅度只有约±50 μgal,约为太阳引力万分之一。
可见,太阳对A点的引潮力就是扣除了太阳引力占99.99%的不变(偏心率不为零时为极缓慢变化)部分后,因地球自转而产生的变化部分,此部分引力的垂直分量,就是重力固体潮,日波、半日波是主要成分。
高精度重力仪可以记录到日月引力作用下,一天中双峰双谷、有清晰相位特征的重力潮,记录曲线讯噪比可超过50分贝(图2)。
正是日月引力的这个微小的变化部分,让探寻引力相互作用的传播速度成为可能。
与光(电磁波)不同,引力是一种相互作用,不能脱离相互作用着的两端的源。对于太阳的引力作用,t时刻测站A的重力潮值,由测站A与地心的位置及日月质心的位置决定。下面以太阳为例,太阳的位置该如何确定?
4. 太阳视位置需作周年光行差校正到真位置
其实,万有引力定律并非不含时间,时间项出现在r中。距离r由相互作用的两质量体的时空坐标计算,时间是必然要参与到运算中的。下面以太阳位置的确定来说明。
由光学仪器在t时刻观测得到太阳在天球上的位置,称为太阳视位置
。太阳光到达地球需要的时间为
分钟,约500秒。太阳光发出时刻的真实位置称为太阳真位置。
在天文观测中,天体视位置要作光行差校正得到天体的真位置,是因为光速有限,而地球以约30 km/s的速度绕日公转。周年光行差角约
角秒。
假设,一年中太阳黄经变化是匀速的,在
分钟中,太阳黄经
变化
角秒。
可见,太阳的光行差改正
角秒是由于太阳视位置与真位置之间的时间差
分钟引起的。计算A测站t时刻重力固体潮理论值,太阳位置要用经光行差校正后的真位置
的时空值。
太阳视位置
与太阳真位置
的黄经相差
角秒,时间相差为
时分。
月亮光到地球的时间
约1s.28时秒,在重力仪目前观测精度下,难以用重力固体潮资料,把月亮的真位置和视位置分辨出来。因此可以忽畧1s.28时秒的时差。月亮的真位置与视位置可以认为重合。
5. 重力固体潮理论包含了引力以光速传播假定
A测站t时刻重力固体潮理论值,太阳位置要用经光行差校正后的真位置
的时空值,太阳引力从
时刻发出,t时刻到观测点A。
如果固体潮观测值的幅度和相位都与理论值相符,就说明重力固体潮理论是反映了客观真实的,也说明引力相互作用传播速度与光速相同。
5.1. 对重力固体潮观测数据在时间域中的分析
若引力瞬间传播,太阳引力从
时刻发出,到观测点A的时刻就不是t而是
,比引力以光速传播早到了约500秒。引力瞬间传播的理论固体潮值,作为引力接收方地球和测站的位置应该用
时刻的值计算。
汤克云 [2] [3] 将中国地震局新疆乌什站PET型弹簧重力仪2009年7月22日的秒采样固体潮观测数据,和固体潮理论计算的理论值及设想引力瞬间传播的理论值比较(图3)。
图3中三条曲线几乎完全重合,但在局部放大的图4中可以看出,三条曲线间有足够明显的时差。图4中三条曲线大致平行,若以观测值为准,观测值滞后光速传播曲线32秒,观测值滞后引力瞬间传播理论曲线141秒。
从地球物理角度,观测值滞后光速传播曲线32秒,可用海潮和地球物质的粘弹性解释。观测值滞后瞬间传播曲线141秒,则无法解释。由此可以初步得出引力瞬间传播的设想是错的,引力以光速传播的假定可能是正确的。
下一步,汤文对观测值作滞后校正,再扣除月潮理论值,分离出太阳潮观测值,与日潮理论值及引力瞬间传播日潮理论值比较(图5),最后得出引力速度与光速的偏差不超过5%的结果 [2] [3] 。
汤文中计算引力与光速的偏差,主要依靠光由太阳到地球需要约500秒时间,PET型弹簧重力仪的采样间隔与之相比要短得多(采样间隔为1秒)。影响计算偏差的主要因素是关于地球介质滞弹性导致固体潮的时间滞后dt ,汤文根据文献 [8] [9] 取dt = 37秒是全球平均值,对某一个具体地方会有误差。乌什和狮泉河站虽然远离海洋,海潮影响相对较小,没有作海潮改正,也有误差。此外,依据一天观测数据在时间域中的分析不能将太阳和月亮的引力分离开,汤文中用观测值扣除月潮理论值,得出太阳潮观测值是不得已的做法。有了长序列观测数据,利用日潮与月潮频率的差异,利用数字滤波等调和分析方法,可以直接将日波S2与月波M2 的相位滞后值分离出来。
可以肯定的是,即使不作介质滞弹性时间滞后校正,仍不支持引力瞬间传播,只是偏差会增大到26%。
汤文中狮泉河、乌什两个站,固体潮观测数据和固体潮理论计算结果符合,与引力瞬间传播理论值

Figure 3. A comparison of three curves of observational solid tides with theoretical values of solid tides and momentary theoretical values of gravitational force on July 22, 2009 in Wushi Station, Xinjiang
图3. 新疆乌什台2009年7月22日固体潮观测曲线与固体潮理论值、引力瞬间传播理论值三条曲线的比较
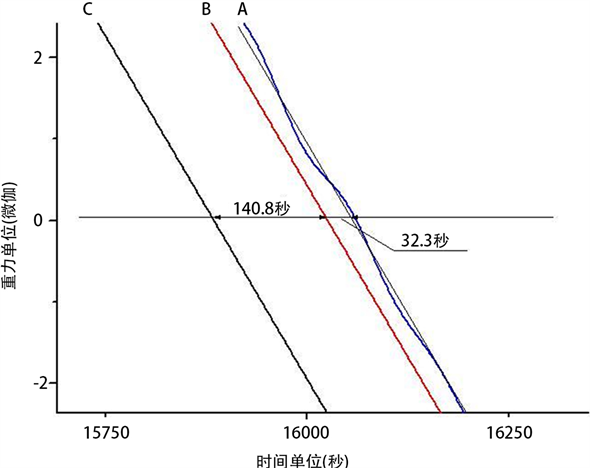
Figure 4. An enlarged view of the partial enlargement box in Fig3 of the observational curve of the earth tide in (A), the theoretical curve of the solid tide (B) and the theoretical curve (C) of the instantaneous propagation of the gravitation. The three curves are roughly parallel. If the observation value is based, the theoretical curve of the solid tide is about 32 seconds ahead of time, and the of the instantaneous propagation of gravity is about 141 seconds ahead of the observational curve
图4. 图3局部放大框中固体潮观测值曲线(A)与固体潮理论值曲线(B)及引力瞬间传播理论曲线(C)的放大显示图。若以观测值为准,固体潮理论值曲线超前观测值约32秒,引力瞬间传播理论曲线超前观测值约141秒

Figure 5. On July 22, 2009, Wushi, Xinjiang, compared the three curves of the daily tide observation curve (A) with the daily tide theoretical value (B) and the instantaneous propagation of the tide’s theoretical value (C) [3]
图5. 新疆乌什台2009年7月22日,日潮观测曲线(A)与日潮理论值(B)、引力瞬间传播日潮理论值(C)三条曲线的比较。此图引自文献 [3]
相差甚远,证明引力相互作用传播速度与光速相同。
5.2. 对重力固体潮长序列观测数据在频率域中的分析
地球固体潮波由日月天体与地球间距离和地球自转、公转周期性变化产生,包括一系列不同频率的波。各种波频率不同,有了长序列观测数据,用数字滤波器将这些波分离,可以求出各波观测值与理论值的振幅比值和相位差。太阳波中以半日波S2振幅最大,月亮波中以半日波M2振幅最大,这两种波振幅因子和相位差的精度高于其它波。
太阳引力产生的半日波S2波,其角速度为每小时走30度。引力瞬间传播时,引力比光早500时秒超前到达地球,500时秒相当于引力瞬间传播的太阳重力固体潮观测值半日波中S2波的相位,比固体潮理论值半日波中S2波相位将超前4.2°。
月亮光到地球的时间
仅
时秒,月亮引力产生的M2波,其角速度为每小时走
度,则
时秒应走
度。假定引力传播速度无穷大,则月亮固体潮观测值比月亮视位置作为理论值的固体潮早到
时秒,在重力仪目前观测精度下,月亮的真位置与视位置可以认为重合。在引力瞬间传播情况下,月亮M2波相位滞后的超前量可视为0°。
中国科学院测量与地球物理研究所孙和平研究员等对武汉站SGC032号超导重力仪重力固体潮资料,对观测结果进行光行差和海潮负荷改正后,给出了各种分潮波的潮汐因子及相位差。表1中资料选取从2000年3月31日到2003年6月15日 [10] 。
表1中第一行为未经海潮负荷改正的调和分析结果,下面11行是经各种海潮负荷改正方法改正后得到的结果,第一列中的SCW80、CSR3.0…是使用的海潮模型名称。
各波下面左边一列数据为观测值与理论值的振幅比,右边一列为观测值相位与理论值相位的相位差,由表1可以看出,月亮潮汐波中的半日波M2波中只有一种海潮改正后相位差为0.22度,太阳潮汐半日波S2波中只有一种海潮改正后相位差为0.27度,其余各方法均小于0.2度。

Table 1. The comparison of tidal parameters before and after tidal load correction in Wuhan station [10]
表1. 武汉台站经海潮负荷改正前(后)潮汐参数间的比较[10]
注:δ为振幅因子(无量纲参数),Δφ为相位滞后(˚)。
观测到的M2波和S2波的相位差都符合固体潮理论相位差为零或接近于零的结论。
若引力瞬发即至,则太阳的引力比太阳光先到地球500秒钟,相当于太阳半日波S2波的观测值比理论值的相位要超前4.2度,但从表中看出S2波观测值与理论值的相位差仅0.2度左右,因此引力瞬发即至的结论不成立。
由表1中还看出太阳波中的S2波观测值与理论值的相位差,基本等于月亮波中M2波观测值与理论值的相位差。月亮的光仅须1.3秒钟到达地球,为什么两者观测值与理论值相位差基本相等,且都接近于零呢?只有一种解释,即太阳光与太阳引力同时到达地球,月亮光与月亮引力同时到达地球才有可能,才有相位差与天体到地球之间距离无关。也说明引力的传播速度与光的传播速度相同。
按理光和引力同时到达地球时,观测值与理论值应没有相位差,表1中列出S2波M2波均有约0.2度的相位差,主要由地球物质非弹性产生,予以扣除后两种波的相位差均应接近于零,残差部分来自海潮改正的不充分和仪器观测精度所限。
海潮负荷改正目前尚未有公认的权威方法和统一的海潮图,表1所列相位差的数值,表现出不同海潮负荷改正方法有较大的差异,M2波、S2波最大最小的相位差之差达0˚.39。表1中所列相位差的数据,没有理由进行取舍。现将表1中M2波和S2波海潮负荷改正后的相位差,分别去除最大值,然后取平均,M2波的平均相位差为0˚.015,S2波平均相位差为−0˚.040,现在以0˚.015作为因地球的粘弹性引起的相位滞后,予以减去,则M2波相位差为零,S2波相位差为
,由于S2波波速为每小时30度,故−0˚.055度相当于6.60秒,与太阳到地球光线传播时间500秒钟相比,为0.013。即引力速度与光速的偏差为1.3%。
不作海潮负荷改正的S2波相位差最大,为
,则引力速度与光速的偏差为9.4%。
选择不同海潮改正方法,引力速度与光速的偏差也不同。但即使不作海潮改正,也不会改变引力以光速传播的论证,只是不确定性增大到10%,仍不支持引力瞬间传播结论。
6. 光行差校正操作,逻辑上隐含:引力速度只能与光速相同
固体潮理论在确定日月位置时需作光行差改正的操作,这一操作从逻辑上再次认定引力速度与光速相同。
太阳作为一个物质实体,同时发出光和引力。太阳的“光源位置”和“引力源位置”自然是一致、重合的。
因为光速有限,地球又以30 km/s速度运动,我们通过光学观测获得太阳的“光源视位置”需要作光行差改正,校正到“光源真位置”。我们认为校正后太阳的“光源位置”和“引力源位置”仍然是一致、重合的。
我们可能忽视了,太阳“视位置”需要作光行差校正的原因是:光速有限。若光速无限,光行差校正角就等于零。对引力也一样,只有引力速度有限,才有“引行差”校正的必要。
我们可以设想,太阳发射“光子”,也发射“引力子”。若要光行差改正后太阳的“光源位置”与“引力源位置”仍重合,只有引力速度与光速相同才可能。
若光速有限引力速度却无限,光行差改正就会出现太阳的“光源位置”移动了
角秒,“引力源位置”却没有移动,光行差改正后太阳的“引力源位置”与“光源位置”就不再重合。
所以,固体潮理论中,天体位置作光行差校正操作,认为校正后的“光源真位置”就是“引力源真位置”,实际上已默认引力速度与光速相同。
总之,若光速有限引力速度却无限,光行差改正就会出现太阳的“光源”位置与“引力源”位置不重合的悖论。
狭义相对论指出,光速是物理作用速度上限。若有某种相互作用速度超过光速,就会出现违反“因果律”等各种逻辑上不自洽的境况。读者不难发现,在我们构建的引力瞬间传播固体潮理论模型中,就存在这类窘境。
结论是:引力相互作用的传播速度只能与光速相同。
7. 结论
科学界一直存在对引力速度的不同看法。
文献 [11] 依据1805年Laplace对月球轨道的稳定性分析,断定引力传播速度至少大于7 × 106 c [12] 。而Flandern于1998年对脉冲双星PSR1534+12的分析给出引力速度的下限值为2 × 1010 c [13] 。而狭义相对论指出,光速是所有物理作用速度的上限。
引力相互作用传播速度成为物理学亟待确定的基本常数。
精密重力仪能够观测到日、月引力导致的重力固体潮幅度及相位变化,引力相互作用的传播速度就有可能测量出来。这一点首先为从事重力固体潮观测且关心引力物理的中国地球物理学家意识到。汤克云团队用重力固体潮观测数据,在时间域中分析,得出引力以光速传播的结论。本文在频率域的分析,再次确认引力速度与光速相同。
现任国际地潮中心指导委员会成员的许厚泽院士来信指出:“固体潮理论是在牛顿力学框架下,基于引力相互作用的牛顿万有引力定律建立的。现在所有的精密固体潮观测结果和理论计算结果是完全符合的,也是自恰的。但由于地球对引潮力的响应并非完全弹性,地球介质的滞弹性将导致此相位差有一微小延迟。”
本文的分析指出:固体潮理论隐含了引力相互作用传播速度与光速相同。正如许厚泽院士所指出的:“现在所有的精密固体潮观测结果和理论计算结果是完全符合的”,得出引力速度与光速相同的结论是有大量观测数据为依据的。
2017年10月,LIGO和室女座探测器在伽玛射线卫星和光学望远镜两秒钟内接收到来自同一方向的引力波信号。这证实了引力波的速度与光速相同。
引力波和引力,有联系也有差别。引力波是波,可脱离“源”传播;引力是相互作用,不能脱离“源”存在。在我们周围,接触更多的是引力的作用。当前,天体力学、人造卫星、宇宙飞船都在应用万有引力定律,但引力瞬间传播的牛顿万有引力定律存在“超距作用”和“不满足洛伦兹协变”两大缺陷。我国科学家在国际上首次测得引力传播速度,是物理学的一个基础性重要结果,据此,物理学家就能正确理解牛顿引力公式,克服上述逻辑缺陷,构建更完善的引力理论。
致谢
感谢中国地震局台网中心提供西藏狮泉河站和新疆乌什站PET型弹簧重力仪固体潮观测数据。感谢中国科学院测量与地球物理研究所孙和平、陈晓东、周江存、郝兴华、周百力先生,提供超导重力仪固体潮观测资料调和分析结果。
作者对许厚泽、滕吉文、李惕培、石耀霖、孙和平、杨志根、刘序俨、郝晓光、徐建桥在问题讨论中提出的质疑和建设性意见表示衷心感谢。