1. 桩-土-结构动力相互作用研究现状
由震源出发通过场地土传播的地震波输入到结构体系使其振动,这时结构体系产生的惯性力如同新的震源又反过来作用于场地,引起场地的变形,使得土–结构体系的交界面的运动不同于自由场地情况,这一复杂的相互作用过程称之为桩–土–结构动力相互作用 [1] 。由于涉及到上部结构、下覆无限地基、桩基础及其组成材料的非线性和远场地面等多种因素影响,因此桩–土–结构动力相互作用成为了高层建筑、桥梁工程、海岸和近海工程建设与设计中普遍关心的问题之一,是结构工程、岩土工程与地震工程的交叉研究领域。研究桩–土–结构动力相互作用的基本规律,对于提高桩基结构的安全性和可靠性具有重要的意义。
桩–土–结构动力相互作用的计算模型一般可以分为直接有限元模型、动力Winkler模型和集中质量模型。其中,直接有限元模型能较好地描述土体中的应力波传播之外,它也具有处理土性的变化和地震动空间变化的灵活性,但该方法计算较为复杂,计算量大、计算时间较长。动力Winkler模型是一种较为简单的线弹性地基模型,模型中真实土体并不出现,而是以力学元件–弹簧、阻尼器代替。动力Winkler模型的关键在于确定弹簧的刚度系数和阻尼器的阻尼系数。由于该模型一般需要利用试验得到的p-y曲线求弹簧的刚度系数,所以在实际桥梁工程的设计中它的应用受到了一定的限制。
集中质量模型是一种使用较早的计算模型,又称作多质点系模型或明德林(Mindlin)静力模型,该模型首先由Penzien教授(l964)提出来 [2] 。桩为弯曲剪切型多质点系,各质点处既有水平位移又有转角。靠近桩体的土与桩体有相同的振动,这部分土体称为等价土体,也被简化为多质点系(称为等价体系),远离结构物的地基,可近似地视为半无限体,它不受结构物存在的影响。其振动以单位面积土柱简化成的多质点系(称为自然地基体系)来描述,只考虑弹性剪切变形。在自然地基与等价体系之间以水平弹簧相连。该模型具有简单方便的优点,而且突出地体现了动力反应分析中最本质的质量、刚度和阻尼三因素,物理概念明确,揭示了动力相互作用的主要矛盾,尽管相对于直接有限法来说有些粗糙,但计算量要小得多,且该法所建立的质量–刚度–阻尼模型的动力平衡方程的解法较为成熟。
2. 集中质量模型参数的确定方法研究
桩–土–结构动力作用集中质量计算模型 [3] 如图1所示。
上述模型中需要确定5个动力计算参数 [4] [5] [6] :
桩土水平相互作用的等价土体刚度
、等价土体阻尼系数
、等价土体质量
、桩周场地质点和自由场模型质点之间的层间刚度
、层间阻尼系数
。
桩-土-结构动力相互作用是一个多学科交叉的复杂课题,笔者旨在给出一种计算模型简单、参数便于确定的实用性方法,以满足实际工程抗震设计需要。
等价土体刚度
和等价土体质量
的确定主要依照现行基础设计规范进行。
本文主要就等价土体的阻尼系数
的确定方法进行了部分改进,将土体的阻尼分成土体材料阻尼和土体辐射阻尼两部分考虑,其中材料阻尼根据土的工程特性试验来确定,而较难把握的辐射阻尼引入了Gazetas和Dobry教授的新研究成果。
另外,对土体自由场分析进行了深入研究,引入了粘性人工边界法,并采用Midas/GTS进行时程分析得到土层的自振频率,从而确定层间刚度
和层间阻尼系数
,提高了计算精度和效率。
2.1. 等价土体弹簧刚度的确定
Penzien通过对半空间理论分析,认为Winkler假定是成立的,因此可按照明德林(Mindlin)公式来求解土-桩相互作用的水平弹簧刚度
,但是该方法计算非常复杂 [7] 。对于实际结构,工程中可根据《公路桥涵与地基基础设计规范》 (JTG-D63 2007),按m法计算弹性桩水平位移及作用效应。每层土弹簧的刚度K可以用下式定义:
第1层土
第2层土
第n层土
式中:
—第n层土的地基水平向系数的比例系数,取值参照公路桥涵与地基基础设计规范(JTG-D63-2007)表P.0.2-1取得。由于地震作用时桩土之间的瞬时刚度一般比静力刚度要大,已有研究表明土层的动力m值一般取静力值的2~3倍较为合理 [8] 。

Figure 1. Analysis model of the lumped mass about pile-soil-structure interaction
图1. 桩–土–结构相互作用集中质量分析模型
2.2. 自由场土层分析
无限地基的模拟是结构–地基动力相互作用分析中的核心问题之一。自由场土层的分析采用Midas/GTS进行,通过自由场土层分析可以得到土层的自振频率和地震作用下土层的剪应变
。目前解决半无限域空间问题最常用方法是在截取的有限域上设置人工边界 [9] 。在众多的人工边界中,最简单的局部人工边界是Lysmer与Kuhlemeyer提出的粘性人工边界。它施加简便并且适用性较强,目前在许多波动问题中得到了广泛应用。
对于土层二维平面应变单元的粘弹性人工边界而言(见图2所示),其等效物理系统的弹簧刚度系数
和阻尼系数
分别为由下式确定 [10] :
法向边界:
;
(1)
切向边界:
;
(2)
式中,
、
分别为弹簧法向与切向曲面刚度(KN/m3);R为波源至人工边界点的距离(m);
、
分别为S波和P波的波速(m/s);G为土的剪切模量(KN/m2);
为土的质量密度(kg/m3);
和
分别为法向和切向的人工边界参数,其中
的取值范围在
,
的取值范围在
。计算表明人工边界参数在一定范围内取值均可以给出良好的结果,一般计算取值为
,
。
2.3. 等价土体阻尼系数的确定
桩–土–结构体系中的阻尼问题将桩、上部结构的结构阻尼与土体阻尼分别进行处理。桩和上部结构的结构阻尼一般可按Rayleigh阻尼理论或者应变能理论计算,对于钢混组合结构而言,通常按照应变能理论考虑。土体的阻尼由材料阻尼Cm和辐射阻尼Cr两部分组成。
土体的材料阻尼比与土体剪切模量的关系一般可表达为:
(3)
式中,
为最大阻尼比,参考日本《道桥示方书–耐震篇》,取值为0.3;G和
分别为土体的剪切模量和最大剪切模量。

Figure 2. Equivalent physical system of viscoelastic artificial boundary
图2. 桩-土-结构相互作用集中质量分析模型
与土体剪应变
之间的关系一般应根据土的工程特性试验来确定,设计时缺乏试验数据时可参考日本《道桥示方书–耐震篇》建议的方法 [11] 。该方法是在标准砂土的
试验曲线的基础上提出的修正公式,即:
(4)
式中,
是
下的依存于
的剪切模量的比值(图3)。
根据临界阻尼理论,可得到土体的材料阻尼系数为:
(5)
式中,m为土的模态参与质量,
为土的一阶自振圆频率,可由Midas/GTS软件计算得到。
根据Gazetas和Dobry教授的研究成果 [12] ,土层的辐射阻尼可表达为下式:
(6)
其中,A为土层的面积,
为土层密度,
为土体泊松比。土体的阻尼矩阵可表达为:
(7)
2.4. 等效土体质量的确定
计算相互作用质量时常采用经验公式,即假定附加土质量
是与承台面积相等、厚度按相应层高的土体质量相同,然后近似将
平均分配到各个桩上。附加土质量
的计算公式如下:

Figure 3. The relationship between
&
and
图3.
及
与
的关系
(8)
式中:
为土的密度;A为承台的面积;
为该层土的层高。
2.5. 层间弹簧刚度与阻尼系数的确定
桩周围场地质点和自由场地模型质点第i层间剪切弹簧刚度
可以由下式确定:
(9)
式中,G为土层剪切弹模;A为桩周土土柱面积,一般取值为承台的面积;
为第i层土层单元厚度。
层间阻尼系数
采用刚度比例型阻尼,由下式确定:
(10)
式中,
为第i层土层阻尼比;
为土层的一阶自振圆频率。
3. 工程实例分析
以广东省江顺大桥工程为例,其主桥跨径布置为60 + 176 + 700 + 176 + 60 m = 1172 m双塔混合梁斜拉桥(模型见图4(a)),下部结构桩基础模型(见图4(b))假定桩侧土是Winkler连续介质,由m法确定土体动力相互作用的水平刚度系数,并用弹簧和阻尼器模拟土介质的动力特性。限于篇幅,本文均以Z3主塔下桩基础为例,并取一般冲刷线以下的第一层土为例计算各动力参数,土层的单元厚度取3 m,根据本桥工程地质勘查资料,这里采用ZQZK9号钻孔柱状图(见图4(c))进行分析,则岩土力学基本参数如表1所示。
1) 等价土体弹簧刚度的确定
桩计算宽度b = 2.45 m,动力m值按照静力m值的2倍考虑。等价土体弹簧刚度系数计算取值如表2所示。
2) 自由场土层分析和等价土体阻尼系数的确定
自由场地土层的分析采用Midas/GTS进行,人工边界的截断宽度取承台宽度的10倍,采用子空间迭代法进行模态分析,然后利用地震安全性评价给出的基岩地震波作为地震动输入进行土层响应时程分析,计算结果如下:
a) 土层自振频率
;
b) 地震作用下,岩石剪应变
基本在0.001~0.002之间,覆盖层土体剪应变在0.01以上,故本桥Z3
 (a)
(a)  (b)
(b)  (c)
(c)
Figure 4. The finite element numerical model; (a) numerical model of the whole bridge; (b) numerical model of pile cap; (c) geological drilling plan of tower
图4. 有限元数值模型;(a) 全桥数值模型;(b) Z3承台数值模型;(c) Z3塔地质钻孔图
主塔下土层的动力参数取值如表3所示:
3) 等效土体质量的确定(表4)
4) 层间弹簧刚度与层间阻尼系数的确定(表5)
5) 桩–土–结构相互作用对结构地震响应的影响
为评估集中质量模型对结构地震响应的影响,将其与工程上2种常用的简化模型(承台底六弹簧模型、等效嵌固模型)做了对比分析。承台底六弹簧模型是在承台底部加上六个方向的弹簧来模拟桩基础的作用;

Table 1. The basic parameters of rock and soil mechanics of Z3 main tower
表1. Z3主塔下岩土力学基本参数

Table 2. Spring stiffness coefficient of Equivalent soil
表2. 等价土体弹簧刚度系数
注:上表中水文对应的一般冲刷线高程位置为−30.8 m。

Table 3. The damping coefficient of soil of Z3 main tower
表3. Z3主塔下土层的阻尼系数
等效嵌固模型是将桩在一般冲刷线以下一定深度处嵌固来处理,等效嵌固深度一般为3~5倍桩径。地震作用下,桩–土–结构动力相互作用的三种模型地震响应对比结果见图5、图6所示。

Table 4. Soil equivalent quality of the pile
表4. 桩周等效土体质量

Table 5. The spring stiffness between layers and damping coefficient
表5. 层间弹簧刚度与阻尼系数
 (a)
(a)  (b)
(b)
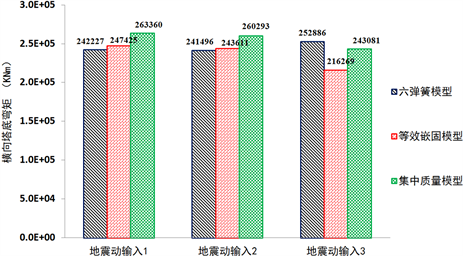
Figure 5. Comparative analysis of three different models with bending moment at tower bottom; (a) Longitudinal bending moment; (b) Transverse bending moment
图5. 三种不同模型中塔底弯矩值的对比(单位,KNm);(a) 纵向弯矩;(b) 横向弯矩
 (a)
(a)  (b)
(b)
Figure 6. Comparative analysis of three different models with bending moment at pile top; (a) Longitudinal bending moment; (b) Transverse bending moment
图6. 三种不同模型中桩顶弯矩值的对比(单位,KNm);(a) 纵向弯矩;(b) 横向弯矩
由图5可见:1) 塔底纵向地震内力大小的规律表现为:六弹簧模型 > 等效嵌固模型 > 集中质量模型,且集中质量模型比六弹簧模型平均小32.6%,比等效嵌固模型平均小28.3%;2) 塔底横向地震内力大小总体上三者差别不大,基本在10%以内;
由图6可见:1) 桩顶纵向地震内力大小的规律表现为:等效嵌固模型 > 六弹簧模型 > 集中质量模型,且集中质量模型比六弹簧模型平均小13.5%,比等效嵌固模型平均小36.5%;2) 桩顶横向地震内力大小的规律表现为:等效嵌固模型 > 六弹簧模型 > 集中质量模型;且集中质量模型比六弹簧模型计算值平均小15.2%,比等效嵌固模型计算值平均小32.5%。
另外,研究发现集中质量模型比其他两种简化模型计算值总体上偏小的主要原因,是由于地基的无限性使得结构振动的部分能量通过波的传播向无限远地基发生散射,通过能量辐射产生辐射阻尼所致,相当了增加了结构体系的总阻尼。
4. 结论
本文重点阐述了桩–土–结构动力相互作用中的集中质量模型若干动力参数的计算方法,并结合某大跨度斜拉桥工程实例,与另外两种常用的工程简化模型进行了比较分析,得到如下结论:
1) 利用m法计算土体的等效刚度,运用粘弹性人工边界法建立土体自由场模型,根据土体的粘滞与辐射阻尼理论建立土体人工阻尼,据此可确定集中质量模型的主要动力计算参数;
2) 不论是纵向地震还是横向地震作用,集中质量模型的内力响应在三种模型中是最小的,且桩顶内力响应值比简化模型最高可小30%左右;
3) 集中质量模型比简化模型计算值总体偏小的主要原因是由于地基的无限性使得结构振动的部分能量通过波的传播向无限远地基发生散射并产生辐射阻尼所致。
基金项目
广东省公路勘察规划设计院股份有限公司委托项目(2011-A14-4),中铁大桥勘测设计院集团有限公司重点课题(2013-16)。