1. 引言
1900年普朗克提出能量常数h假设,1905年爱因斯坦将普朗克常数h作为光子的能量常数,1924年,德布罗意 [1] 提出物质波假设,将普朗克常数h引入粒子或物质波计算公式。德布罗意认为光子的动量
,光子的波长
,并推导出物质波波长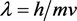 ,或
,其中m、E为实物粒子的质量、能量;实物粒子的频率
,角频率
,波矢
,其中
。依据德布罗意假设,自由粒子平面波函数
,或
,其中m、E为实物粒子的质量、能量;实物粒子的频率
,角频率
,波矢
,其中
。依据德布罗意假设,自由粒子平面波函数
(1)
式中A为平面波振幅,i为复数形式,
为约化普朗克常数,
为粒子动量矢量,
为粒子的空间位置矢量,E为粒子能量(动能),t为粒子从初相位到末相位时间。
德布罗意关于物质波的思想是正确的,但是将普朗克常数h作为所有基本粒子和实物粒子的能量常数是值得商榷的。普朗克常数h实际上是电子的能量常数,不是光子的能量常数 [2]。用德布罗意公式计算光子波长、动量和能量有较大误差;用德布罗意公式计算实物粒子的波长、频率、角频率和波矢等都有较大误差。
1926年,薛定谔 [3] [4] [5] [6] 将德布罗意物质波引入波函数理论,提出基于经典理论的波函数方程,描述粒子的波动性、运动状态和量子化性质,揭示粒子运动的基本规律。如一般情况下粒子微分运动薛定谔方程
(2)
式中
为能量算符
,哈密顿量算符
,其中
为动能算符
,拉普拉斯算符
,
为势能。
定态薛定谔方程
(3)
式中
为不显含时间的稳定势场,E为能量算符,如玻尔原子模型中电子定态能量,
为H的本征函数。
1926年,玻恩 [7] [8] 对薛定谔波函数进行统计诠释,认为薛定谔波函数是粒子几率波函数,论述了薛定谔波函数的合理性。
薛定谔波函数的一个基本假设,将普朗克常数h作为量子力学体系的特征量,引入到波函数方程。由此推导出能量算符
、动量算符
、哈密顿量算符
、动矢量
、波矢
和角频率
,影响到整个波函数的形态,影响到薛定谔波函数方程求解的精确性。基于经典理论和德布罗意物质波推演的薛定谔波函数及其波动方程有较大的局限性。
薛定谔方程是量子力学的一个基本假定,在量子物理、原子物理、等离子物理、核物理、电磁波理论、分子物理等领域得到广泛应用 [9]-[18]。在实践中薛定谔方程不易精确求解,很多学者提出薛定谔方程的数值求解方法,如差分方法 [19]、谱方法 [20]、有限元方法 [21] 及其他的方法等等。正因为如此,薛定谔方程的应用也受到极大限制。
本文目的在于建立基于相对论的粒子波函数方程,直接用于粒子实验数据计算,描述粒子运动的物理实在。论述与粒子波函数相关的基本粒子波长原理和基本粒子运动路径波动原理,将粒子静止质量常数 [2] 引入爱因斯坦运动粒子质能方程,将粒子的运动质量引入牛顿动能方程,提出相对论动量算符
、能量算符
以及哈密顿量算符
,将薛定谔方程修改为相对论粒子波函数方程。通过光子双缝洐射实验,检验证明相对论粒子波函数方程中的位置矢量
就是粒子波动路径矢量
。并通过氢原子辐射实验数据,对氢原子电子波函数与几率波进行检验计算,证明基于
的统计解释符合氢原子电子运动的物理实在。
2. 粒子波函数的相关概念
基本粒子以及实物粒子具有波粒二重性。薛定谔方程通过粒子几率波揭示粒子运动的波动属性,但是还没有充分解释粒子波动的本质。
2.1. 基本粒子波长与外场能量密度波长
基本粒子是具有一定能量密度的自旋体 [22] ,在具有一定能量密度的外场中运动。所谓基本粒子波长,是指在一定密度能量场中运动的具有一定质量的基本粒子能量场边缘的能量密度,即基本粒子能量场半径外切点的能量密度。基本粒子在不同密度的能量场中有不同的波长,能量密度越大,波长越短,反之越长。基本粒子的半径与其运动速度有关,速度越大,半径越短,反之越长。基本粒子的运动速度与其质量有关,同时与路径上的外部能量场的能量密度有关。光子由于质量很小,在大于光子静止质量波长的能量密度中可以自动产生位移运动,在真空中接近光速c。电子及其他粒子,由于质量较大,只有在具有势能差的外场中才能产生位移运动。基本粒子在不同外部能量场运动有不同的半径,这就是运动粒子的能量场半径。氢原子从核心至外缘,能量密度从大至小呈梯度分布。这一梯度能量场,可以用能量密度波长进行刻画,一定的能量密度与一定的波长一一对应。氢原子外层电子吸收一个光子向外层跃迁,由于受原子核的吸引而回落,并辐射光子,在某一辐射点,电子有一定波长,辐射光子有同样波长,辐射点的能量密度也有同样波长。氢原子光谱的每一条光谱线非常精确地反映了辐射点运动电子的波长
和辐射光子的波长
,刻画了辐射点能量密度波长
。基本粒子波长揭示粒子的粒子属性。运用粒子波长可以计算粒子的静止质量、运动质量、动量和能量等相关变量。
2.2. 基本粒子波动与外场势能波动
所谓基本粒子波动,是指运动中的基本粒子与外部能量场的相互作用而产生的波动。外部能量场由原子、分子、固体、流体,以及真空构成。基本粒子本身也互为外部能量场。基本粒子在外部能量场运动,有一定的波长、动量、能量、速度,也有一定的运动路径。运动中的基本粒子是一个自旋球体梯度能量场,并融入外部能量场,随外部能量场的起伏而波动。不同波长的光子通过透明晶体或气体走不同能量密度的路径,在入射点发生折射,在出射点出现色散。不同速度的电子有不同的波长,通过一定能量场,也会发生折射和散射。基本粒子在均匀能量场中走直线,在非均匀能量场中不走直线,即产生波动。如金属晶格是非均匀能量场,电子在金属晶格中运动产生波动;空气分子晶格是非均匀能量场,光子在空气分子晶格中运动产生波动。能量场的均匀与非均匀是相对的,从原子、分子层面看是非均匀的,从原子集合体、分子集合体层面看是均匀的。如光子在空气分子晶格中波动,波幅小于1纳米,不易察觉和测量。因此,人们的经验是光子在空气中、水体中以及透明晶体中走直线。基本粒子在晶格中波动,有波幅和波长。显然,基本粒子波动波长与基本粒子波长是不同性质的。基本粒子波动波长揭示粒子的波动属性。
2.3. 基于相对论的粒子波长与动量
1900年,普朗克提出的能量常数h,实际上是电子的能量常数。普朗克常数h与电子静止质量
、电子能量E、康普顿电子波长
之间的关系,
,
,
。1905年,爱因斯坦提出质能关系式
,电子的静止质量转换成能量
,所以
,
。康普顿电子波长
是计算电子静止质量的波长。因此,依据基本粒子的波长(如各种光子的波长)计算其静止质量是合理的。粒子的质量也是量子化的,用粒子静止质量常数
[22] 和粒子波长计算粒子静止质量
(4)
将基本粒子的静止质量与体积大小统一起来计算
(5)
式中
为精细结构常数,
为基本粒子半径,
。
玻尔氢原子基态电子波长是电子在基态的运动波长,基态电子的等效速度为精细结构常数乘以光速,
。氢原子外层电子的等效速度
(6)
式中
为氢原子外层电子运动波长,
为氢原子外层电子基态波长。式(6)符合相对论要求,可以代入洛仑兹公式进行计算。玻尔氢原子基态电子波长
,
(7)
式中
,是电子波长(康普顿电子波长
)与基态电子波长之比。依据粒子的静止质量,可以计算粒子的波长和基态波长。粒子以不同的速度运动,有不同的粒子运动波长。氢原子外层电子运动波长
(8)
由于电子辐射光子,电子运动波长
的值在实验中是可以测量的。普朗克常数h是电子的能量常数,电子的动能
(9)
在原子中,电子的等效速度不可能超过基态电子速度,但运用强磁场可以加速电子。当电子运动波长
接近两倍康普顿电子波长
时,电子速度接近光速。当电子速度
,电子运动质量
是电子静止质量
的
倍。依据电子运动波长计算电子运动质量与总质量
(10)
(11)
依据电子运动质量计算电子的动能
(12)
在低速情况下式(10)计算结果,与牛顿动能方程
计算结果基本一致。当电子速度大于基态
电子等效速度,甚至接近光速时,前者计算结果远远大于后者计算结果。实物粒子的运动质量很小,牛顿动能方程只考虑了实物粒子的静止质量,没有考虑实物粒子的运动质量。事实上,无论实物粒子还是基本粒子,在运动中都是质量(磁量子)的相对位移,都增加相应的运动质量。粒子运动加速,运动质量增加,反之减少,粒子运动终止,运动质量瞬间转化为能量全部释放。因此,电子的动能
(13)
式(12)计算结果与式(13)计算结果的比值r接近1。这一比值可以对式(13)的值进行修正,即
(14)
如果用下式计算电子动能
(15)
随着粒子速度接近光速,式(12)计算结果与式(15)计算结果的比值r接近2。这一比值可以对式(15)的系数“1/2”进行修正,即
(16)
式(16)实现了牛顿动能方程思想与爱因斯坦运动粒子质能方程思想的统一,揭示了基本粒子和实物粒子运动质量、动能和能量的本质。因此,电子动量
(17)
式中
。
以上计算电子静止质量、电子波长、电子波长半径、速度、电子运动波长、动量、动能等公式,完全符合相对论要求,具有普遍意义,可以用于基本粒子和实物粒子相关变量的计算。计算举例见表1。
3. 基于相对论的粒子波函数
将粒子静止质量常数引入爱因斯坦运动粒子质能方程,将粒子的运动质量引入牛顿动能方程,提出相对论动量算符
、能量算符
以及哈密顿量算符
,可将非相对论薛定谔方程修改为相对论粒子波函数方程。
3.1. 基于相对论的动量、能量与哈密顿量算符
粒子平面波方程中动矢量
,来源于德布罗意关系式
。薛定谔方程中
,
其中
,动量算符
。粒子动量
,并且有
,m为粒子的静止质量。

Table 1. Data table of particle rest mass, Particle wavelength, Particle wavelength radius, velocity, energy, momentum, Particle motion wavelength and de Broglie wavelength
表1. 粒子静止质量、粒子波长、粒子波长半径、速度、能量、动量、运动波长、德布罗意波长数据表
式中没有考虑粒子的运动质量,在低速情况下p值误差不大,但在高速情况下p值误差较大。当然实物粒子不会获得高速,但基本粒子可以获得高速,光子在真空中具有光速,电子、质子通过加速可以接近光速。
薛定谔方程适合低能粒子
、
相关波函数分析,不适合高能粒子波函数分析。粒子的半径、运动速度、运动波长、位置、动量、动能等相关变量,是相互协变的。运用粒子变量相互协变关系式,可将低能与高能粒子的波函数分析统一起来,完善波函数方程。依据式(5)、(6)、(11),电子动量
(18)
,
(19)
令
(20)
则有
,
,
(21)
式中
为相对论动量算符,
为相对论能量算符,
为相对论哈密顿量算符,其中
为粒子
动能算符
,
为粒子势能。
3.2. 基于相对论的粒子波函数方程
薛定谔方程是基于经典理论的波函数方程,与牛顿方程等价。运用相对论动量算符
,相对论能量算符
,相对论哈密顿量算符
,可将经典的薛定谔方程修改为相对论粒子波函数方程。相对论自由粒子平面波函数方程
(22)
式中
为动量算符因子,
为自由粒子波动路径矢量。
相对论三维情形平面波归一化波函数方程
(23)
一般情况下相对论粒子微分运动波函数方程
(24)
相对论定态波函数方程
(25)
式中E为波函数粒子定态能量,
为束缚粒子的势能。
4. 杨氏双缝实验对波函数的检验
粒子波函数揭示了粒子运动的基本规律,粒子的波函数方程描述了粒子运动的基本形式,粒子运动几率波描述了粒子运动的基本形态。杨氏双缝实验科学地检验了粒子运动的基本规律、基本形式和基本形态。但是,人们过去对杨氏双缝实验的分析,还存在很多不完善的地方。本文试图予以更合理解释。
4.1. 双缝的折射与反射原理
杨氏双缝实验的基本原理,一个粒子离开发射源,经过均匀空间到达双缝中的任一缝,通过窄缝发生弹性折射或反射,再经过均匀空间到达屏幕,形成一个衍射点,无数个衍射点组成粒子分布的波函数状态。下面以光子杨氏双缝实验为例。
双缝衍射原理,是光子的磁量子体通过双缝不对称能量场发生弹性折射或反射,改变运动路径的波动形式。双缝前后是由氧气等分子组成的空气分子晶格体。组成窄缝的材料由原子或分子构成,密度大于空气密度,窄缝两壁有类似原子或分子的梯度能量场,因此,窄缝两边能量密度大,中间能量密度小。窄缝中间有很窄的空气分子晶格体,与窄缝前后空气分子晶格体连通。单缝两壁的梯度能量场是对称的。光子是具有自旋的能量体,能量密度由内至外呈梯度分布,通过单缝时会受到窄缝壁梯度能量场的影响而改变方向,发生一定角度的反射或折射,形成单缝衍射条纹。双缝中两条缝的能量场是对称的,而每条窄缝的两壁梯度能量场不对称,中间壁梯度能量场略小,因此,光子通过双缝中的任一窄缝增大了偏向双缝中央的折射角和反射角,偏中二分之一个条纹,即光子的半个波长,中间亮条纹是光子波长顺序的逆向重合,两边条纹是顺向重合,形成双缝衍射条纹。
光子在空气分子晶格体中运行,窄缝前后由空气分子晶格行列组成窄缝面,光子从不同的列入射窄缝,有不同的折射率或反射率。窄缝的出射光子与入射光子在原本连通的空气分子晶格中产生偏移,中间条纹没有晶格偏移,随着条纹级数增加,晶格偏移增多。光子通过窄缝,可能居中通过,也可能偏左或偏右通过,发生弹性碰撞折射或反射,只要离开窄缝梯度能量场,立即获得空气中的光子的速度。离开窄缝梯度能量场的光子都有确定的波长、动量、能量和路径。
光子通过窄缝发生反射还是折射,由光子的自旋方向决定。光子偏向窄缝左壁入射,并且左旋,则向左折射,右旋则向右反射;光子偏向窄缝右壁入射,并且右旋,则向右折射,左旋则向左反射。光子在窄缝壁的反射和折射是对称的。光子通过窄缝,以特定角度入射至空气分子晶格中,入射晶格在窄缝中央。窄缝有大有小,缝小,入射晶格列少;缝大,入射晶格列多。所以,缝的大小决定衍射条纹多少。相同的入射角和入射晶格,接收不同波长的光子,不同波长光子在空气中走直线,但有不同的折射率,形成色散,即形成彩色条纹。单缝或双缝衍射的彩色条纹,包含可见光以外的紫外光和红外光,是空气分子晶格体可色散的序列光谱,两级单色条纹之间的距离等于两级彩色条纹中相同单色波长之间的距离。
4.2. 粒子的路径波与波函数方程
粒子的波动是粒子的运动属性,是粒子在运动中与路径上的能量场相互作用的运动形式。如光子在空气分子晶格中,经过一系列分子排列的直线上面,在每一个晶格中都走最短时间路径,光子经过一个分子的上面形成波峰,经过两分子之间的上面形成波谷。这种波是光子(粒子)的路径波,波长与路径上分子(粒子)直径相对应。
所谓粒子路径波,是指粒子在运动路径上经过一系列粒子(原子、分子等)能量场而产生的波动。光子经过分子(或原子)梯度能量场,离分子中心(或原子核)有一定距离,波长越短,距离越小,反之则大。因此,不同波长的光子在均匀与非均匀介质中,都走自己的最短时间路径。相对论自由粒子平面波函数方程和一般情况下相对论粒子微分运动波函数方程中的位置矢量
就是粒子波动路径的矢量
。双缝实验揭示了光子路径波的现象与规律。
在双缝实验中,光子通过空间和窄缝,有特定的路径,可以用波函数来描述。光子通过窄缝能量场和窄缝前后的均匀空间,无须外力作用,没有能量衰减,是理想的自由粒子,可用相对论自由粒子平面波函数方程和一般情况下相对论粒子微分运动波函数方程描述其运动波长、动量和路径;加速后的电子通过空间和窄缝,动量略有衰减,可用一般情况下相对论粒子微分运动波函数方程和相对论自由粒子平面波函数方程描述其运动波长、动量和路径。
4.3. 量子态迭加原理
根据海森堡原理 [23] ,粒子不能同时占据同一位置。两个以上基本粒子同时出现在某一体元
,是一个“凝聚”体,是粒子的迭加态,或量子迭加态。单缝或双缝实验中,同波长、同自旋方向、同折射角(或反射角)的多个光子(或一束光子),入射窄缝的同一行列空气分子晶格,会走同一波动路径,从宏观上看走同一直线。在波动路径上,这些光子不能同时占居同一位置,但相互接近形成迭加态。一束光子中某一体元是该体元内所有光子体积的迭加,一束光子中某一体元的动量是该体元内所有光子动量的迭加。如果某一体元较大,可以包含许多不同波长光子的迭加。粒子的迭加态波函数也称为波包
。
在一般情况下,
不是平面波,依据Fourier分析 [24] ,将
表述为平面波的迭加。用平面波归一化三维情形波函数方程描述
(26)
其中
(27)
式中
为波幅,与动量相关,
为自由粒子波幅。
4.4. 粒子的几率波函数
从双缝衍射的光子,无论是一个接一个衍射,还是多个光子同时衍射,与双缝平行的一系列衍射平面上(包括观察屏幕的平面),都有光子的分布状态,而且一系列光子分布状态都是一致的,反映粒子在路径上的分布状态或几率分布的不变性。从缝1和缝2衍射出来的同波长同方向同出射角的光子没有聚焦点,运行的“直线”路径是平行的。在大于以双缝间距为直径的路径体元内,通过缝1或缝2的光子处于迭加态
,几率
。
从双缝衍射的每一个光子都有确定的波长、体积、动量、动能和路径。光子的分布状态可用波函数
描述,即t时刻在空间
处体元
内光子出现的几率为
,其几率密度为
。
几率波函数是基于物理实验的波函数,相关物理实验揭示基本粒子的相关物理现象与规律,或者说几率波函数描述基本粒子运动的现象与规律。人们对一些复杂事件不十分了解,或者一时不可能了解的情况下,将一个事件的出现当作随机事件,并用大量随机事件来揭示事物运动的现象与规律。这当然是科学的。但是,当人们对复杂事件有更多的了解和认知,发现一些“随机”事件的出现也有它的必然性。在单缝或双缝实验中,一个粒子之所以衍射到屏幕的P点,是由一系列因素决定的,主要包括光源、窄缝、空气分子晶格体。光源发射的光子,有确定的波长、辐射角、自旋方向,会辐射到窄缝特定的位置的空气分子晶格,并有相应的折射或反射,再衍射到屏幕的P点。在实验中,只要光源辐射稳定,窄缝确定,空气分子晶格体不变,衍射条纹就是稳定的。衍射条纹间接反映光源发射的光子的分布状态,甚至间接反映光源发射体的材料结构及其性质。
5. 氢原子辐射实验对波函数的检验
氢原子由一个质子和一个电子组成,自旋的质子磁量子体带动自旋的电子磁量子体旋转。氢原子在没有被激发的情况下,电子处于基态。氢原子受到激发,或电子吸收光子,电子发生跃升,退激时则回落,即电子在质子自旋带动的路径上波动。电子在质子梯度能量场波动,在确定时刻有确定的波长、动量和动能,有确定的路径和位置。氢原子辐射实验能精确检验外层电子的波动及其波函数。
5.1. 氢原子的吸收与辐射
氢原子的吸收与辐射,《普朗克常数与光子静止质量常数统一实验分析》 [2]、《基于粒子自旋的原子模型与实验分析》 [22] 进行了较具体的阐述。氢原子在没有其他激发的情况下,基态电子吸收一个极紫外线光子后,电子跃升至第二能级
,由于受质子吸引开始回落,相继释放莱曼线系光子。如果氢原子在受到一定的稳定的磁能或热能激发情况下,电子跃升至第二能级
,处于相对稳定态,此时电子再吸收一个紫外线光子,电子跃升至第三能级
,由于受质子吸引开始回落,相继释放巴耳默线系光子。氢原子其他线系吸收与辐射同理。
光电效应与氢原子的电子吸收与辐射同理。《普朗克常数与光子静止质量常数统一实验分析》 [2] 式(16)、(20)中应去掉
项。光电效应实验中电子跃迁至阳极,初始动能很小,此时受到阳极电势吸引,到达阳极板。
5.2. 氢原子外层电子波函数方程
氢原子基态或相应能级稳定态电子跃升至外层,受到质子吸引,有一个势能。这个势能等于外层电子受原子核吸引回落到基态(或某一相对稳态
)所做的功。处于基态或相对稳定态的电子的势能为零。基态电子或相应能级稳态电子吸收一个同等能量的光子后产生跃升,然后回落。电子在回落的路径上,不同时点都有不同的波长、动量和动能,波长变短,动量和动能增加,势能减小。氢原子外层电子势能
(28)
式中V的单位为J,
,b为维恩位移定律常数,单位为mK,
为基态电子或相应能级稳定态电子波长,
为外层电子的运动波长。下式也可计算电子的势能
(29)
式中电子基本电荷
,单位为焦耳/1伏特 [2] ,真空电容率(基于新的基本电荷计算值)
,电子离核半径
,其中
。氢原子外层电子波动方程
(30)
式中
用球对称中心力场表示
,在原子核自旋中
心磁场约束下,电子在原子的
轴平面随着原子核旋转,
趋于
。
5.3. 氢原子外层电子几率波
氢原子基态电子或相应能级稳定态电子,吸收一个相应能量光子产生跃升,然后释放相应系列光子。由于电子在回落的路径上确定时刻具有确定的波长并释放同波长光子,所以一系列辐射光子波长的变化反映了电子运动波长的变化。无论电子跃升与回落,原子核带动电子运动的路径接近测地线。电子跃升与回落,在不同时点有不同的等效速度,即相对于原子外参考系,电子在围绕原子核运动,随着离核半径减小,等效速度增大。氢原子基态半径或相应能级稳定态半径圆面积内没有电子出现几率。不同线系的辐射光子反映不同线系辐射路径上电子出现的几率。下面以巴耳默线系为例,描述氢原子定态波函数与动量几率波函数,见表2。
氢原子巴耳默线系稳定态电子吸收一个紫外光子,产生跃升,在回落过程中辐射一系列光子。本表取前5个光子波长和稳定态电子波长数据 [22] ,规定电子在路径上
处体元等于一个电子体积,依据本文相关公式计算获得表中数据。表中
为辐射光子波长,
为辐射点电子波长,
为辐射点能量密度波长,均与电子波动路径矢量
相关。
为氢原子定态波函数电子动能算符,V为电子势能,E为稳定态电子能量。
、E为原子核束缚能,取负值。
为电子动量算符,与波函数
相关。
描述电子在
处的振幅,揭示电子的波动属性,
描述电子在
处体元
出现的几率,揭示电子的粒子属性。基于
的统计解释及波函数归一化分析
,符合氢原子电子运动的物理实在。
6. 结论
薛定谔方程将普朗克常数
作为量子力学体系的特征量,在实践中不易精确求解。本文目的在于建立基于相对论的粒子波函数方程,直接用于粒子实验数据计算,描述粒子运动的物理实在。首先,阐述粒子波长和粒子运动路径波动概念。论述粒子波长揭示粒子的粒子属性,粒子路径波动揭示粒子的波动属性。将粒子静止质量常数引入爱因斯坦运动粒子质能方程,将粒子的运动质量引入牛顿动能方程,实现两者的统一,共同揭示基本粒子和实物粒子运动质量、动能和能量的本质。其次,修正德布罗意波关系式的误差,提出相对论动量算符
、能量算符
以及哈密顿量算符
,并引入波函数方程,将薛定谔方程修改为相对论粒子波函数方程。再次,通过光子双缝洐射实验,指出光子在空气分子晶格中波动,通过双缝不对称能量场改变其折射率或反射率,不同波长的光子在不同路径上波动,从而检验证明相对

Table 2. Data sheet of Hydrogen atom Palmer line system steady-state wave function and electron momentum probabilistic wave function
表2. 氢原子巴耳默线系定态波函数与电子动量几率波函数数据表
论粒子波函数方程中的位置矢量
就是粒子波动路径矢量
。最后,通过氢原子辐射实验数据,对氢原子电子波函数与几率波进行检验计算,证明基于
的统计解释符合氢原子电子运动的物理实在。基于相对论粒子波函数对量子物理的发展与应用将具有重要作用。
NOTES
*通讯作者。