1. 引言
本文考虑一个反映扩散系统:
(1)
其中
,
是R中的开区间,
和
,是定义在开子集
上的矩阵值函数,
,
,
是从
到
的光滑映射。
我们先来看一下不变区域的定义(见文献 [1] [2] [3] [4] )。
定义1:闭集
称为(1)的局部解的(正)不变区域,如果
的初值和边界均属于
,且对于
,满足
。
其中不变区域
可由“半空间”的交集组成,即
(2)
其中
是定义在开子集U上的光滑实值函数,并且
。
通过不变区域的定义我们得到(1)的整体存在性定理(见文献 [4] )。
定理1:设B是可容许的巴拿赫空间,
,对于
,(1)的解在
上有先验估计:
即对于
,(1)在
上有解
。证明见文献 [4] 。
2. 不变区域的主要内容
定义2:光滑函数
在
点称为是拟凸的,若
,则推出
其中
。
定理2:设
由(2)定义给出,假设对任意
并且
(对于i有
),满足以下条件:
1) 对
,在
处是
和
的左特征向量。
即存在
有
2) 如果
,
,则
在
点是拟凸的。
3) 对
在
点
。
则对于每一个
,
是(1)的不变区域。
此定理证明见文献 [1] 。
定义3:称方程组的初边值问题(1)是f稳定的,如果对于f的任意函数列
,只要在有界闭集
上,
一致收敛于f,
一致收敛于
,那么v存在时,当
时,
也存在。同时在
的稠密集上,存在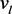 的子列收敛到v。其中
的子列收敛到v。其中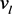 和v分别是问题(1)对应于
和v分别是问题(1)对应于 和f的解。
和f的解。
注:如果方程组(1)是f稳定的,我们可以将定理2的条件3)放宽至:
3)' 对 在
在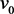 点
点 。
。
其他条件不变,则定理1仍成立。
推论1:假设D和M都是对角矩阵,并且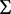 满足下面式子:
满足下面式子:
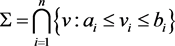 (3)
(3)
还需满足定理1中的条件3),即f在 处指向
处指向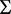 内部,则对于
内部,则对于 ,(3)是方程组(1)的不变区域。
,(3)是方程组(1)的不变区域。
下面给出应用不变区域的例子,并且通过定理1研究解的整体存在性。
例1:三级食物链模型
实物A为昆虫或者植物,中级猎物B为食饵或鸟类,和高级猎物C,且B只吃A,C只吃B,没有B,C将死掉,没有A,B和C都死掉,记u,v,w分别是A,B,C的分布密度,则三级食物链反应扩散方程为:
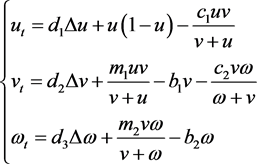 (4)
(4)
这里的所有参数都是正常数。详见文献 [5]
我们令 ,
, ,
, ,
, ,
, ,
,
设 ;
;
则(4)可写成 。
。
由推论1我们设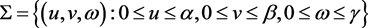 ,下面证
,下面证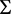 是不变区域。
是不变区域。
则
 ,
, ,在
,在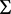 内部,所以有
内部,所以有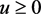 ;
;
 ,
,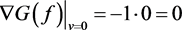 ,在
,在 内部,所以有
内部,所以有 ;
;
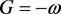 ,
, ,在
,在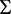 内部,所以有
内部,所以有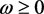 ;
;
 ,
,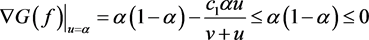 ,在
,在 内部,所以有
内部,所以有 ;
;
 ,
,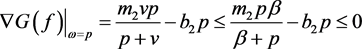 ,在
,在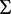 内部,所以有
内部,所以有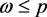 ;
;
 ,
,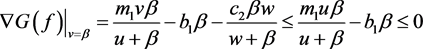 ,在
,在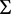 内部,所以有
内部,所以有 。
。
综上可知,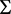 是不变区域。因此由定理1可知只要初值在可容许的巴拿赫空间内,可以得到三级食物链模型解的整体存在性,因此通过构造任意大的区域,当初值不同时,可以分析各个物种生存情况。
是不变区域。因此由定理1可知只要初值在可容许的巴拿赫空间内,可以得到三级食物链模型解的整体存在性,因此通过构造任意大的区域,当初值不同时,可以分析各个物种生存情况。
例2:二聚自催化化学聚合物模型
A为M的同分异构体,M为单体,Rj为传播者,P是表示二聚物,则反映扩散模型为:
 (5)
(5)
其中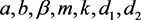 是正参数,变量
是正参数,变量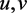 表示浓度或密度。详见文献 [6]
表示浓度或密度。详见文献 [6]
下面证明此反应扩散方程有不变区域。
证明:设 ,
,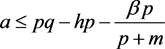 ,
,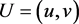 ,
,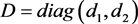 ,
,

则(5)可写成 。由推论1可知,我们设
。由推论1可知,我们设

接下来我们证 是不变区域。
是不变区域。
 ,
,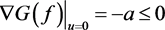 ,在
,在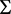 内部,所以有
内部,所以有 ;
;
 ,
, ,在
,在 内部,所以有
内部,所以有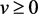 ;
;
 ,
,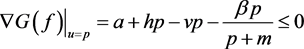 ,在
,在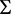 内部,所以有
内部,所以有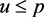 ;
;
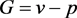 ,
, ,在
,在 内部,所以有
内部,所以有 。
。
综上,由定理2可知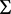 是不变区域。同样二聚自催化化学聚合物模型也可以通过构造任意大的区域来研究两种浓度(密度),只要初值在可容许的巴拿赫空间内,由定理1可知(5)的整体解存在,因此可以通过改变反应物量的多少来研究其产生的化学现象。
是不变区域。同样二聚自催化化学聚合物模型也可以通过构造任意大的区域来研究两种浓度(密度),只要初值在可容许的巴拿赫空间内,由定理1可知(5)的整体解存在,因此可以通过改变反应物量的多少来研究其产生的化学现象。
例3:Gray-Scott模型
 (6)
(6)
 代表两种反应物的反映浓度,
代表两种反应物的反映浓度,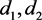 为
为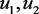 的扩散系数,第一步的反应速率为1,第二步的反应速率为a,b为反应物输入反应容器的流速。详见文献 [7] 。
的扩散系数,第一步的反应速率为1,第二步的反应速率为a,b为反应物输入反应容器的流速。详见文献 [7] 。
下面证明此系统有不变区域。
证明:设 ,
,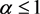 ,
, ,
,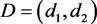 ,
,

则(6)可写为 。由推论1,我们设
。由推论1,我们设
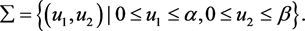
 ,
,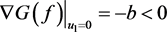 ,在
,在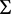 内部,所以有
内部,所以有 ;
;
 ,
,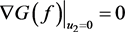 ,在
,在 内部,所以有
内部,所以有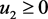 ;
;
 ,
, ,在
,在 内部,所以有
内部,所以有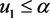 ;
;
 ,
, ,在
,在 内部,所以有
内部,所以有 ;
;
综上所述,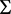 是不变区域。
是不变区域。
例4:(见图1)我们考虑下面这个例子(见 [8] ):
 (7)
(7)
这里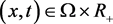 ,
, ,
, ,带有边界条件
,带有边界条件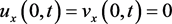 ,很容易得出
,很容易得出 是(7)不变区域,我们取
是(7)不变区域,我们取 ,
, ,其中
,其中 为常数,方向向量
为常数,方向向量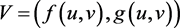 ,“+”和“−”代表V中各自函数在它们零集合边上的符号。从图中我们能看出V在
,“+”和“−”代表V中各自函数在它们零集合边上的符号。从图中我们能看出V在 指向
指向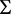 的内部。因此我们可以构造任意大的矩形区域来研究当初值位于可容许的巴拿赫空间时,(7)的整体解的存在性,随着f的增加,g的量在减小,从图中我们也可以看出,在p点两种量达到平衡。
的内部。因此我们可以构造任意大的矩形区域来研究当初值位于可容许的巴拿赫空间时,(7)的整体解的存在性,随着f的增加,g的量在减小,从图中我们也可以看出,在p点两种量达到平衡。
3. 结语
通过这几个例子,我们可以看出,以上四个模型具有不变区域,之后可以通过构造任一大的不变区域来研究解的整体存在性,从而更好的分析初值在此区域的发展趋势,对于研究生物和化学方面的规律有一定的作用。