1. 引言
无线通信系统的飞速发展对数据传输的可靠性提出了更高的要求,因而各种高能效可靠传输技术成为了无线通信研究的热点,其中协同传输技术备受关注。作为一种有效的差错控制技术,协同自动重传请求(C-ARQ)协议以其可靠的数据传输而被广泛地应用和研究 [1] [2] 。
无线信道往往面临着信号衰落,我们一般会建立有限状态的Markov链的分析模型来刻画衰落信道,从而研究无线通信的数据传输情况和通信系统的性能。文献 [3] 提出了一种基于两状态的马尔科夫链的Gilbert Elliott信道模型,将信道定义为两种状态,即“好”(Good)状态和“坏”(Bad)状态,这种模型也成为后续研究的一种基本方法。文献 [4] 提出了带有单中继的ARQ系统的三状态Markov模型,分别以完全相关的瑞丽衰落信道和完全不相关的瑞丽衰落为背景讨论了ARQ系统的吞吐量性能,得出影响吞吐量的三个因素:信道是否相关、中继节点位置、链路的衰落余量。文献 [5] 提出了一种节点协同的停等式ARQ方案(NCSW),通过Gilbert Elliott信道理论将M个中继节点等效成一个超级中继节点,进而分析了系统的吞吐量和时延性能。文献 [6] [7] [8] [9] 将Gilbert Elliott信道模型和有限Markov链模型运用到了多跳ARQ系统,其中文献 [8] 中Maymouna Ben Said等人提出了带有译码和发送(DF)中继的多跳ARQ系统的三状态Markov模型,并根据中继是否丢包对两跳ARQ系统的吞吐量性能进行了分析,不足之处是对于大于两跳的多跳ARQ系统,并没有给出完整的吞吐量分析。
本文基于以上研究的成果,对大于两跳的多跳ARQ系统的中继节点是否丢包进行了分析,进一步研究了系统的吞吐量性能。首先,我们将 [8] 中多跳ARQ系统在中继节点不丢包的状况下得到的吞吐量进行了修正;然后通过建立多跳ARQ系统的三状态Markov链模型,得到了多跳ARQ系统在中继节点不丢包的状况下通信系统吞吐量的解析式;最后,我们考虑了中继节点丢包的状况并设定了丢包的临界中继,通过多跳ARQ系统的三状态Markov链模型求得吞吐量的解析式。本文的主要结果为判断中继节点是否应该丢包提供了可靠地理论保障。
2. 记忆信道模型
本文假设所有的信道均为瑞丽衰落信道,对于衰落信道最常见的研究方法是建立有限状态的Markov链的分析模型。在实际的网络中,特别对于衰落信道来说通信通常是有“记忆”的,信道传输数据成功与失败之间往往存在短暂的相关性,所以这里我们采用两状态的Gilbert Elliott信道模型来建模突发信道,从而很好地描述这种“记忆”性和相关性。
如图1,为Gilbert Elliott信道模型,我们设定物理信道有两个状态:G (Good)状态和B (Bad)状态。如果数据包被成功接收,信道处于G状态;否则,信道处于B状态。我们用X(k)表示信道在k时隙的状态,则有:
(1)
这里,
表示所给定信道在k时隙的信噪比(SNR),
是信噪比的一个门限值。
若信道在当前时隙处于G状态,在下个时隙信道仍保持G状态的概率我们表示为
,则信道在下个时隙由G状态转为B状态的概率为q;同样的,若信道在当前时隙处于B状态,在下个时隙信道保持B状态的概率我们用
表示,则信道由B状态转向G状态的概率为r。即有:
于是,两状态的Markov过程的概率转移矩阵如下:
根据平稳状态方程,求得信道平稳时信道处于B状态的概率:
(2)
根据文献 [5] ,在瑞丽衰落信道中有:
(3)
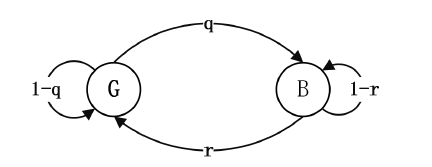
Figure 1. Gilbert Elliott channel
图1. Gilbert Elliott信道
这里
,F是信道的衰落余量,由(2)和(3)可以得到q和r的关系:
(4)
其中概率r见文献 [8] :
这里,
是马坎Q函数,
为第一类零阶贝塞尔函数,
是多普勒频率。由信道的衰落余量F和多普勒频率
,我们就可以计算出转移概率r和q的值,从而很好地描述这种两状态的Markov链模型。而节点X和Y之间的信道的衰落余量我们用
表示:
(5)
其中,
是节点X和Y之间链路的信噪比的期望,同样的
、
是节点X和Y之间链路的长度和噪声的方差,
是指节点发送每个符号消耗的能量,
(常数)为距离的衡量尺度,
是路径损耗因子,取值一般在2~4之间。
3. 多跳ARQ系统的三状态Markov链模型及系统吞吐量的分析
在这部分,首先定义我们研究的多跳无线系统具有N个中继节点:
,如图2示,并假设每个中继节点只能侦听相邻的两个中继节点,每个中继节点只能和相邻的节点进行数据包的传送。
下面我们将从以下两种情况计算系统的吞吐量:
① 中继节点将数据包发送之后,仍保留有数据包的副本,即中继节点不丢包的情况;
② 中继节点将数据包发送之后,不再保留数据包,即中继节点丢包的情况。
对于每一种情况,我们都建立了三状态的Markov链模型,通过建立的模型导出了系统的吞吐量。
3.1. 中继节点不丢包的三状态C-ARQ协议
协议的工作原理如下:
① 节点S同时向目的节点D和第一个中继节点
发送新的数据包。
② 如果中继正确接收了数据包,它会告知源节点。
③ 如果目的节点D正确接收了数据包,它会向源节点S和中继节点同时发送ACK应答,然后,源节点S又会进行一个新的数据包的传送。
④ 如果目的节点D和中继节点
都没有正确接收数据包,源节点S将会重传这个数据包。
⑤ 如果目的节点D没有正确接收数据包,但中继
正确接收了,目的节点D将发送NACK应答给源节点S,中继
将承担发送任务,他会向中继
发送此数据。
⑥ 如果
没有正确接收来自
的数据包,中继
将会向
发送NACK应答,同时
向
重新发送此数据包。
⑦ 如果中继
正确接收了数据包,它将承担起传送任务,然后将此数据包发送给中继
。
⑧ 重传过程往往会重复出现,直到传送的数据包被目的节点D正确接收。
根据协议的运转,并结合Gilbert Elliott的两状态信道模型,定义出系统在k时隙的三个状态,如下:
状态①:一个新的数据包由源节点S发送,nT。
状态②:源节点S重传数据包,Rs。
状态③:中继节点
重传数据包,Rr。
由上述分析,可以建立中继不丢包时多跳ARQ的三状态Markov链模型,如图3。
相应的概率转移矩阵为:
(6)
设系统处于平稳状态时的分布为:
,根据平稳状态方程:
解得系统的吞吐量:
(7)
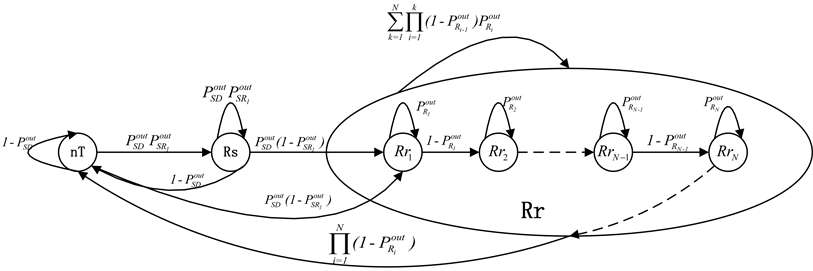
Figure 3. Three-state Markov model for C-ARQ with no packet drop at the relay
图3. 中继节点不丢包时C-ARQ系统的三状态Markov链模型
3.2. 中继节点丢包的三状态C-ARQ协议
我们这里讨论的丢包,不是全体中继都丢包,而是把所有的中继按照它们的位置分为两部分,而划分的临界中继是第
个。也就是说前
个中继是丢包的中继,从第
个到第N个是不丢包的中继。
协议的工作原理如下:
① 节点S同时向目的节点D和第一个中继节点
发送新的数据包。
② 如果中继正确接收了数据包,它会告知源节点。
③ 如果目的节点D正确接收了数据包,它会向源节点S和中继节点同时发送ACK应答,然后,源节点S又会进行一个新的数据包的传送。
④ 如果目的节点D和中继节点
都没有正确接收数据包,源节点S将会重传这个数据包。
⑤ 如果目的节点D没有正确接收数据包,但中继
正确接收了,目的节点D将发送NACK应答给源节点S,中继
将承担发送任务,他会向中继
发送此数据。
⑥ 如果
没有正确接收来自
的数据包,当
时,中继
会向
发送NACK应答,同时
向
重新发送此数据包;否则,源节点S将会重传这个数据包。
⑦ 如果中继
正确接收了数据包,它将承担起传送任务,然后将此数据包发送给中继
。
⑧ 重传过程往往会重复出现,直到传送的数据包被目的节点D正确接收。
系统在k时隙的三个状态同A。前
个中继丢包时多跳ARQ的三状态Markov链模型如图4。
同样,得到其相应的概率转移矩阵:
(8)
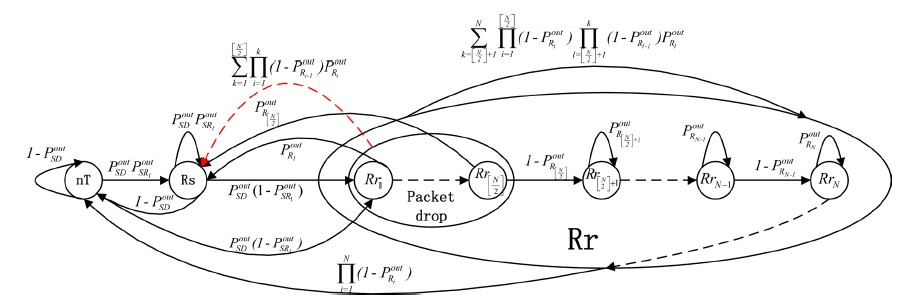
Figure 4. Three-state Markov model for ARQ system with packet drop at first
relay
图4. 前
个中继丢包时C-ARQ系统的三状态马尔科夫模型
设系统处于平稳状态时的分布为:
,根据平稳状态方程:
解得系统的吞吐量:
(9)