1. 引言及文献综述
市盈率 [1] 指标在股票市场中不仅可以用来判断风险的大小,也可以用来预测公司未来的收益。因此,广大投资者经常使用市盈率来确定股票价格水平、估计股票风险的大小;市盈率也能够说明企业获取利润的能力及公司价值增长的可能性,所以金融监管部门可使用市盈率指标来制定相应的监管措施,绝大多数投资人也可使用市价盈利比率来寻找实现资产价值增值的机会。
市盈率最早的定义是1943年格雷厄姆(Graham)和多德(Dodd) [2] 在《证券分析》一书中提到:“一般情况下,一只普通股票的市价是它当期税后收益的倍数,这个倍数或乘数的大小一方面取决于当时的人气即广大投资者,另一方面取决于企业自身的影响”。Loughlin [3] 对1968年到1993年标准普尔500指数的市价盈利比率影响指标的分析得知,市价盈利比率与股息支付率及预期每股增长都呈正向关系。最早应用回归模型分析市盈率影响因素的是美国学者Whibeck和Kisor [4] ,他们使用来自纽约银行的1962年6月份的135只股票数据分析影响市价盈利比率的三个变量:股息支付率、每股收益率和风险。回归分析结果是股息支付率、每股收益率与市盈率具有正相关关系,风险与市盈率具有反向关系。Fairfie1d [5] 阐述了市价盈利比率的经济内涵,认为市价盈利比率越高,未来超额盈余的增长率就越高。他使用美国1970年到1984年的数据证实了这个假设,并根据净资产倍率、市盈率将全部的股票分成9组,分析了各组股票的经济特性及它们将来5年还在原组合的可能性,说明市盈率能够预测未来股票价格与价值。Penman [6] 使用Feltham-Ohlson模型探讨了市价盈利比率的理论本质及它与现在的或者将来的净资产收益率的关系,并对美国1968年到1986年公司的财务数据研究得知,市盈率由现在的和将来的净资产收益率一起作用,并且与现在的净资产收益率具有反向相关,与将来的净资产收益率具有正向相关性。
市盈率指标是度量股票投资价值以及一国股票市场发展完善与否的一个重要依据,因此,我国越来越多的学者也对它的影响因素进行定量和定性的研究。李社环等 [7] 使用美国1997年股票市场的数据实证研究了企业负债率和市价盈利比率间的关系,得知企业负债率与股票市盈率具有反向关系。何治国 [8] 使用了中国股票市场1995年5月到1999年5月的数据,实证分析了各种风险因素与股票资产组合收益率间的关系,得知BV/MV对风险的贡献度高于β系数对风险的贡献度,而且BV/MV和市价盈利比率具有负相关关系。曾晓洁等 [9] 分析了上海股票市场、深圳股票市场1993年到1999年的数据得知,股票市场市盈率大体上和公司潜在的成长能力具有正向关系。除此之外,中国股票市场市价盈利比率对下一年的公司成长状况会有很好的预测作用,但第三年之后各年度的成长状况对市价盈利比率没有显著性影响。白娜等 [10] 应用2001年5月22日中国股票市场的数据对上证30指数的市价盈利比率实施了研究,发现β系数对市价盈利比率没有显著性影响;股息支付率与市盈率的相关系数大于每股收益增长率与市价盈利比率的相关系数。这些文献中大都采用个别因素对市价盈利比率的影响,没有综合考虑。本文将综合考虑多个因素,采用多元线性回归模型考虑多个因素对市盈率的综合影响。
2. 研究设计
2.1. 研究方法
普通最小二乘法 [11] (Ordinary Least Square, OLS)在回归分析中,要研究一个变量受到其他因素影响的情况,通常是进行线性拟合,拟合的标准就是在欧式空间下的点到直线之间的距离即对于拟合的这条直线到所穿过的所有点的距离和最小,这样得到的线性方程称为回归方程。OLS的原理如下:
为了使样本回归函数“尽可能的接近”总体回归函数,就是使样本回归函数
估计的
与实际的
的误差尽量小,也就是说,使剩余项
越小越好。可是
有正有负,其简单代数和
会相互抵消而趋于零。为了处理方便,可采用剩余平方和
最小的准则,假设
为第i次观测样本
,即:
根据微积分中求极值的原理,要使
达到最小,待定系数
应满足以下条件:
即:
(1)
(2)
(3)
注意上述各式中括号内的各项恰好为残差
,从而上式k个方程可写成如下形式:
(4)
或者表示为:
(5)
从而通过整理方程组,计算出待定系数
。
2.2. 数据说明和研究变量的选取
由于上证180指数样本股每半年调整一次,因此,本文选择2011~2015年的具有连续相关数据的上市公司作为总体,然后再利用SRS抽样的方法从上证180指数中随意选取34只股票作为样本数据进行实证分析。为了保证研究数据的有效性,提高研究结果的准确性和可靠性,本文根据以下原则对2011~2015年具有连续相关数据的总体进行筛选:去掉样本中市盈率非常大的公司;去掉样本中连续2年没有盈利,并进行特殊处理的股票;然后再利用SRS抽样的方法从上证180指数中任意选取34只股票,所使用的样本观测值都是连续5年数据的均值,目的是为了避免某一年的数据具有较大的偏差而影响最后结果的准确性与可靠性;分析时使用的是所选样本发布的2011~2015年的年度报表数据。本文样本观测值的全部数据都来自于上海证券交易所官方网站。经过查找文献资料与实际的炒股经验,本文首先选取了7个指标因素对市盈率的影响进行分析,然后通过具体的实际数据再研究我们选取的这7个因素对市盈率的有无明显影响,最后通过多元线性回归分析再把其中的无相关因素剔除掉,再对市盈率影响比较大的因素进行分析,最终得到我们的结论。
本文研究的被解释变量与解释变量的具体定义和计算公式如表1所示。
2.3. 实证模型
这部分内容设定了3个多元回归模型来证明选取的八个指标对市盈率的贡献度。其中模型I是包含所有解释变量的总多元回归模型,通过对总回归模型的结果分析,可以得出假设成立与否;模型II是从模型I中选取相关系数和显著性水平较高的
、
、
三个影响指标设定的模型;模型III是从模型II中选取相关系数和显著性水平较高的
和
两个指标设定的模型。

Table 1. Variable definition and calculation formula
表1. 变量定义与计算公式
其中:市盈率(Y),资产负债率(X1),净利润增长率(X2),净资产收益率(X3),股息支付率(X4),每股净资产(X5),行业平均市盈率(X6),每股收益增长率(X7),流通股比例(X8)。
模型I:包含全部解释变量的模型,分析全部解释变量对市价盈利比率的贡献度。
(6)
上式中:
:估计常数项,
:估计回归系数,
,
:估计残差项。
模型 II :根据模型 I 的结果分析得到影响市盈率的三个主要指标,利用这三个主要指标建立新的多元回归模型,分析它们对市价盈利比率的影响程度。
(7)
上式中:
:估计常数项,
:估计回归系数,
,
:估计残差项。
模型 III :由模型 II 的结果可知,相关性较高、显著性较强的两个指标,构建新的多性回归模型,分析它们对市价盈利比率的影响程度。
(8)
上式中:
:估计常数项,
:估计回归系数,
,
:估计残差项。
3. 沪深股市股票市盈率影响因素实证检验
3.1. 中国沪深股市总体市盈率分析
为了对中国沪深股市总体市盈率进行分析,在中证指数有限公司网站整理的有关2016年5月份A股市场主要板块的市盈率数据如下。
从表2中的数据得知,到2016年5月份,沪深A股最新静态市价盈利比率为19.57倍,比近期一个月的平均静态市盈率降低6.94%,其中上海A股最新静态市盈率14.12倍,比近期一个月平均静态市盈率降低5.36%;深圳A股最新静态市盈率38.21倍,比近期一个月平均静态市盈率降低13.20%;在这段时间内,A股指数大体上在3200点左右变动,其中有多只股票刷新了历史记录,甚至远远高于2007年A股6124点时的价格。以上数据显示,即使2016年5月份整体A股市盈率比最近一个月平均静态市盈率有所下降,并不是由于全部A股股票价格下降导致的,而是因为沪深两市中大盘蓝筹股股票价格下将所导致的。数据表明,深市主板最新静态市盈率为23.62倍,比近期一个月平均静态市盈率降低11.77%;中小板最新静态市盈率为46.71倍,比近期一个月平均静态市盈率降低14.26%;创业板近期静态市价盈利比率为69.45倍,比近期一个月平均静态市价盈利比率降低17.73%。

Table 2. P/E ratio of A-share main board in May 2016
表2. 2016年5月份A股市场主要板块市盈率
数据来源:中证指数有限公司。
3.2. 中国沪深股市市盈率波动分析
对中国沪深股市市盈率波动 [12] 情况进行分析时,为了便于观察故利用上海证券交易所统计年鉴2005~2014年度的数据绘制出的沪市A股平均市盈率的柱状图如下图1所示。
从柱状图可以看出,2005~2014年10年间,沪市A股市价盈利比率大体上都在10到35倍间震荡。2007年不断上涨达到股票市场最顶点时,市盈率超过35倍,刷新了以往的记录达到59.24倍。2008年世界金融危机爆发之后,中国的经济受到巨大的影响,特别是股票市场受到的影响也是巨大的,因此,沪市A股市盈率迅猛下降到2008年的14.86倍。2009年虽然有所上升,但还是在20倍左右震荡。在2009年以后,逐年有下降的趋势,但每年的下降幅度不是很大,虽2014年有所上升,但市盈率只有15.99倍,仍在20倍附近。
为了便于对中国沪深股市市盈率波动情况进行分析,故利用深交所统计年鉴2006~2015年度的数据绘制深市股票平均市盈率和主板A股市盈率的变化趋势折线图如图2所示。
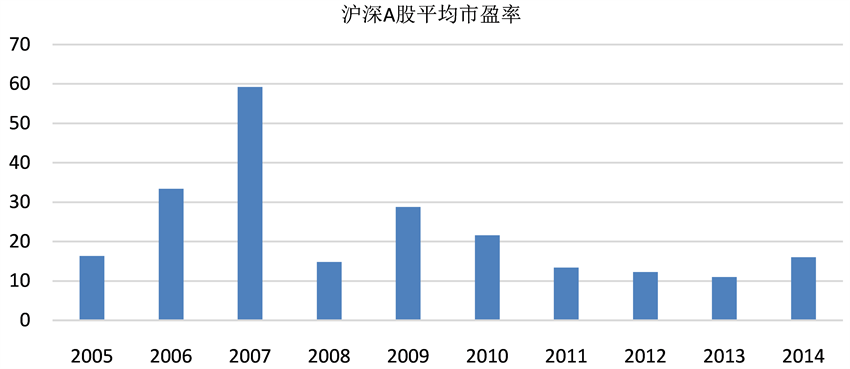
Figure 1. Average P/E ratio of Shanghai A-share in 2005-2014
图1. 沪市A股平均市盈率2005~2014年
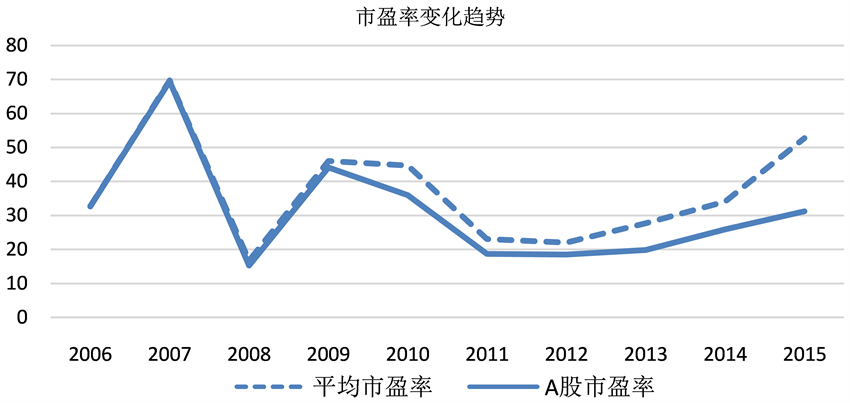
Figure 2. Average P/E ratio of Shenzhen stock market and the change trend of P/E Ratio A-Share main board in 2006-2015
图2. 深市股票平均市盈率和主板A股市盈率变化趋势2006~2015年
分析图2中的变化趋势知,深圳证券交易市场A股平均市价盈利比率和主板A股市价盈利比率大体上以40倍为中线波动,除2008年具有较大的变动幅度,下降到16.72倍外,其它的大体上不变。2007年深圳股票指数创造了以往的新高度,市盈率也超过了以往的最高点,达到了69.74倍,之后随着股票市场的下降而迅猛地下降到2008年的16.72倍,2009年和2010年变动幅度不大,大体上在40倍左右震荡,2012年以后又有所下降,基本上在25倍左右震荡,然而2015又上升到52.75倍。
3.3. 模型的回归结果分析
3.3.1. 模型I的回归结果分析
回归结果分析的原假设:
:
模型I:包含全部解释变量的模型,分析全部解释变量对市价盈利率的贡献度。
(9)
上式中:
:估计常数项,
:估计回归系数,
,
:估计残差项。
根据表3中的数据,模型估计的结果写为:
分析模型的结果得到:
1) 根据回归系数的正负,可以判断Y与
间是正相关还是负相关,即回归系数为正,它们间就是正相关,回归系数为负,它们间就是负相关。在0.05的显著性水平下,一般情况下,t值大于2,P值小于0.05,就说明解释变量对被解释变量具有显著性影响。
Y与
经证明具有弱反向关系,因为
的回归系数为−0.28,且在0.05的显著性水平下,t值和P值没有通过假设检验。
2) Y与
具有正向关系,因为
的回归系数为0.056,且在0.05的显著性水平下,t值和P值没有通过假设检验,因此,可以认为Y与
之间不存在相关关系。

Table 3. Multivariate regression estimation results of model I
表3. 模型I多元回归估计结果
3) Y与
之间的关系经证实具有弱反向关系,因为
的回归系数为−1.12,且在0.05的显著性水平下,t值和P值没有通过假设检验。
4) Y与
具有反向关系,因为
的回归系数为−0.33,而且在0.05的显著性水平下,t值和P值检验是通过假设检验的。
5) Y与
之间的关系经证实具有弱正相关关系,因为
的回归系数为−5.44,且在0.05的显著性水平下,t值和P值没有通过假设检验。
根据结果分析可知,股息支付率的t值为2.15,P值为0.02,在0.05的显著性水平下拒绝原假设
,即
,说明股息支付率对市盈率有显著性影响;行业平均市盈率的t值为3.59,P值为0.011,在0.05的显著性水平下拒绝原假设
,即
,说明行业平均市盈率对市盈率有显著性影响;每股收益增率的t值为2.089,P值为0.025,在0.05的显著性水平下拒绝原假设
,即
,说明每股收益增率对市盈率有显著性影响。
3.3.2. 模型II的回归结果分析
根据模型 I 选取相关系数和显著性水平较高的
、
、
构建新的线性回归模型II:
(10)
上式中:
:估计常数项,
:估计回归系数,
,
:估计残差项。
根据表4中的数据,模型估计的结果写为:
根据结果分析得知,股息支付率的t值为0.13,P值为0.89,在0.05的显著性水平下接受原假设
,即
,说明
对Y没有显著性影响;行业平均市盈率的t值为2.61,P值为0.01,在0.05的显著性水平下拒绝原假设
,即
,说明行业平均市盈率对市盈率有显著性影响;每股收益增长率的t值为3.28,P值为0.02,在0.05的显著性水平下拒绝原假设
,即
,说明
对Y有显著性影响。
3.3.3. 模型III的回归结果分析
根据模型 II 选取相关系数较高的行业平均市盈率、每股收益增长率,构建新的线性回归模型:
(11)
上式中:
:估计常数项,
:估计回归系数,
,
:估计残差项。
根据表5中的数据,模型估计的结果写为:

Table 4. Multivariate regression estimation results of model II
表4. 模型II多元回归估计结果

Table 5. Multivariate regression estimation results of model III
表5. 模型III多元回归估计结果
综合上述模型 III 的多元回归分析,行业平均市盈率的t值为2.61,P值为0.015,在0.05的显著性水平下拒绝原假设
,即
,说明
对Y有显著性影响;每股收益增长率的t值为3.48,P值为0.021,在0.05的显著性水平下拒绝原假设
,即
,说明
对Y有显著性影响。
3.3.4. 模型回归结果总体分析
拟合优度检验结果如下:模型I中的
,
,说明模型对样本的拟合度很好,即本文选取的8个指标对市盈率变化的解释度为84.41%,也就是说,市盈率变化中没有被解释的部分为15.59%,而没有被解释的15.59%是由随机扰动项导致的。模型II中的
,
,说明模型对样本的拟合度很好,即对模型I的回归结果分析得到的三个主要的影响指标对市盈率的变动的解释度为78.95%,则在模型I的8个指标对市盈率变化的解释度中,模型II中的三个指标(
、
、
)的解释能力占93.53%。模型III中的
,
,说明模型对样本的拟合度很好,即用模型II结果中显著性水平最高和相关性大的两个指标对市盈率的变化的解释度为68.90%。若把模型的解释度分离开来进行分析,则可认为模型II中的三个指标对市盈率变动的解释度中,模型III的两个指标的解释能力占87.28%。
4. 研究结论
本文对所选取的影响我国上市公司股票市盈率水平的八个指标进行多元回归分析,得出下面的研究结论:
1) 不同的指标对市盈率的贡献度是有差异的。从回归分析结果来看,资产负债率、净利润增长率、净资产收益率、每股净资产、流通股比例这些指标对市价盈利比率的解释作用不明显,无论是在总体回归模型还是在分回归模型中,行业平均市盈率和每股收益增长率两个因素对市价盈利比率的影响程度和解释能力都比较高。
2) 模型从实证方面证明了它达到了预期的结果,广大投资者可使用模型来推算某只股票的市盈率。在使用回归模型时,广大投资者可依据自己了解的行业状况来选取恰当的模型,但无论选取这3个模型中的哪一个模型,投资者都应把重心放在行业平均市盈率、每股收益增长率两个指标上。
3) 在合理运用的前提下,市盈率可很好地应用于投资决策,多元回归模型分析结果的误差率就很好地证实了这一点。所以,广大投资者在决策时可依据估算的市盈率知道哪只股票可以购买或者持有,从而为自己实现资产价值增值做出理性的计划,而不是毫无目的的进行投资。
致谢
本文是教育部人文社会科学一般项目“金砖四国股票市场成长能力比较研究”(11YJEGJW001)的研究成果之一。