1. 引言
很多同学都喜欢乐器,这是因为不仅乐器演奏出来的声音使人愉悦,弹奏乐器的过程也使人专注或放松。这些声音是如何产生的,大家都知道与物理学知识有关。
确实,不同的物理发声机制决定了不同乐器的分类:1) 弦乐器:包括钢琴、吉他、提琴、琵琶、古筝等。其发声原理为:弦乐器的发音方式是使拉紧的弦振动发音,弦乐器通常用不同的弦演奏不同的音,有时则须运用手指按弦来改变弦长,从而达到改变音高的目的。2) 管乐器:包括长笛、萨克斯等。其发声原理为:吹孔气鸣乐器管体为圆柱型,嘴唇振动时,气流冲击在吹孔锋利的边缘上而分开,进入管中的气流就引起管内空气柱振动而发音。3) 打击乐器:包括架子鼓、云锣、编钟等。其发声原理为:乐器受打击时,发生振动,从而产生声音。
可见,三种乐器的发声原理不同,其背后的物理原理也不尽相同。但是现在的大学物理中 [1] ,很少系统地介绍发声的相关知识,使人难以系统了解乐器发声的基本物理原理。现有的文献中也多以乐器展开 [2] [3] [4] [5] ,没有系统介绍乐器发声的物理原理,使人遇到相关物理知识时感到有些凌乱。本文首先系统介绍基本物理原理,然后依据物理原理具体分析几种典型乐器发声的不同机理,从而对乐器发声的基本物理原理有比较全面的认识,真正认识到物理学是乐器原理的基础。
2. 乐器发声的基本物理原理
2.1. 拉紧弦的波速公式
由杨氏模量公式,拉紧弦中的波速v传播公式为公式(1)。
(1)
其中,FT为弦的张力,µ为弦的线密度。显然,弦一定时,张力越大,波速越大;张力一定时,弦的密度越大,波速越小。
2.2. 弦的驻波解
考虑到弦乐器的弦是两端固定的,其波动只是在这个区间,是驻波解。假定弦两端的距离是L,最大驻波解的波长λ1 = 2L,二级驻波解的波长λ2 = L,三级驻波解的波长λ3 = 2L/3……,n级驻波解的波长λn = 2L/n。这一结论可由图1表示。
由图1可以看出:驻波的基波(n = 1)波长最大,级数n越高,波长越短。弦长与n级驻波解的波长的关系为公式(2)。
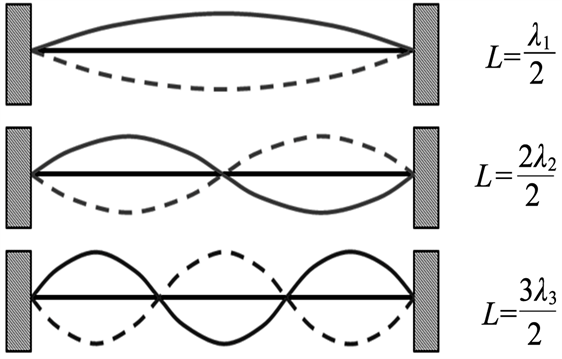
Figure 1. Solution of standing wave with fixed chord
图1. 固定弦长的驻波解
(2)
由公式(1)得知,对于同一根没有改变的弦,各种频率振动的传播速度相同,由频率f = v/λ得知,驻波的基频(n = 1)最小,级数n越高,频率越大。n级驻波解的频率与基频的关系为公式(3)。
(3)
2.3. 乐音(或拍频)
拍频是声波干涉加强或减弱的结果,假定两声波在空间某点相遇时的振动为公式(6),则其合成的振动为公式(7):
(4)
(5)
其中,x1、x2分别是两声波在某点相遇时的振动位移,A为振幅,f1、f2分别是两声波的频率。这样,拍频fb的大小为公式(6):
(6)
图2是拍频形成示意图。其中,f1 = 10 Hz、f2 = 10 Hz,拍频fb = 10 Hz。
2.4. 声波的谐振(共鸣)
声波是纵波,所以无所谓波峰或波谷,只要波程差半个波长,声波叠加就是最大,形成谐振。但这一现象又分为封闭管和开放管,见图3。
1) 封闭管:封闭管中声波需要经过一个往返形成半个波长的波程差,形成共鸣。这样,形成驻波的最大波长是:
(7)
2) 开放管:开放管中声波需要经过半个波长的波程差,形成共鸣。这样,形成驻波的最大波长是:
(8)

Figure 2. Schematic diagram of beat frequency formation
图2. 拍频形成示意图

Figure 3. Propagation of sound waves in closed tubes
图3. 封闭管中声波的传播
以上的波长是共鸣的最大波长,其频率称为基频,乐器产生的频率可以是基频整数倍。另外,如果管长L发上变化,波长也会变化,从而导致频率变化。向暖瓶里倒水,空气管长L变小,由公式(7),声波波长变小,频率变大。有经验的人,根据声调的变化,就能判断出暖瓶水快满了。
2.5. 其他经验公式
实际过程中,影响声波传递和频率的因素很多,以下常见的两个公式。
1) 声波在空气中的传播速度与温度有关,温度越高,传播速度越大。以摄氏为例,0℃时,声速约为331 m/s,温度每升高1℃,速度增加0.6 m/s,可用公式(9)表示。
(9)
其中,v(t)是t摄氏度时声波的传播速度,v(0)是0摄氏度时声波的传播速度,α = 0.6是一常数,由公式(9)可知,温度为20℃时,声速度增加为334 m/s。
2) 打击乐器中板的振动频率。由于板可以看为二维刚体,其振动频率受板的形状、刚性、密度、尺寸和敲打方式等多重因素决定,其基频公式就是一个很复杂的形式,见公式(10) [3] 。
(10)
其中,fmn是第mn次的音频,脚码m、n表示两维阶次,h为板的厚度,r为圆板半径,ρ是材料的密度,μ是泊松比,βmn是与第mn次的泛音有关的系数。
3. 几种典型乐器发声的基本物理原理
3.1. 弦乐器
吉他、小提琴、钢琴是弦乐器的代表。人们称钢琴为乐器之父,小提琴为乐器之母,古典吉他为乐器王子。
吉他和小提琴类似,是靠琴弦发声,主要依据公式(1)、(2)和(3)。首先,依据公式(1)可以得出两个结论:弦一定时,张力越大,波速越大,对于基波或同级数的波,其频率会变大;张力一定时,弦的线密度越大(琴弦变粗),波速越小,其频率会变小。其次,依据公式(2) (3),可以得出:当整条琴弦都在振动发声时,基频的波长大,会发出频率比较低的声音;当按住琴弦的某点,琴弦与琴颈上的金属丝接触,琴弦的下半段形成了一段新的可以产生震动的封闭区间,即公式(2)中的L变小了,这时拨动琴弦,琴弦发出的基频波长变小,频率变大,因此音调也就要高一些。对于其他同级数的音也是如此。
钢琴作为“乐器之王”,它具有音域非常广、音量很大,一根琴弦被击打,其他的弦会同时受到影响发出谐波,使演奏有很好的表现力等特点。钢琴的奥妙虽然多,但归根结底主要还是琴弦的功劳。钢琴有很多条琴弦,不同的琴弦产生了不同的声音。由公式(1)和(3)可以得出:弦长越短、张力越大、密度越小、直径越细,音调越高。
弦乐器和其他乐器一样,不仅会发出基频波,也会发出高级数的谐波,由公式(4)和(5),这些波在空间叠加就会形成和谐的乐音,乐音的频率由公式(6)决定。
3.2. 管乐器
管乐器也是乐器中的一大家族,主要有各种形状的管状体和激声系统构成,它们的共同特点是通过管中空气柱振动作为声源,所以其主要依据是公式(7)或(8),即通过改变空气柱振动的长度,改变驻波的波长。
但是木管乐器和铜管乐器的机理还不尽相同:木管乐器为了获得不同的音调,通过在管体开孔,手指的按压控制孔的开闭的方式,可以改变管的内振动的空气柱长度,从而改变驻波的波长。其中,吹口与外界相连的是闭管乐器,适应公式(7);笛子与萧等乐器不止吹口处与外界相连,属于开管乐器,适应公式(8)。而铜管乐器多使用活塞,通过活塞得伸缩,灵活地空气柱长来控制。
当然,若将闭管乐器简化为一段开口的管,理论上管长应等于四分之一波长;但管口外的一小段空气也会参与管内空气的震动,使得实际参与震动的空气柱比管长要长。若根据理论计算值确定每个音高对应的空气柱长度,音调会偏低。因此在制造管乐器时,需要添加一个管口校正量∆L。由公式(9)得知,当温度变化时,会导致振动传播的速度变化,从而导致乐器的音调发生微小变化。
3.3. 打击乐器
借助捶打、敲击等方法可以使物体发声,打击乐器就是利用这种方式发出乐音的乐器。典型乐器有各种各样的鼓,木琴,编钟等。那些是靠膜振动发声的传统的鼓,振动方程很复杂,公式(10)是假设板振动以刚性作用为主,板的基频公式,实际因素比公式(10)复杂的多。
4. 结束语
物理学是研究物质基本运动现象和规律的基础科学,在科技和生活中各个方面都有应用,在音乐方面也是一样。通过本文可以看到,乐器的发声、音调和音色,以及乐器的制作和调整方法,都与物理原理有关。了解乐器中的物理原理,对乐器不仅知其然,更知其所以然。同时,读者也领会到物理的基础作用。
NOTES
*第一作者。
#通讯作者