1. 引言
水驱特征曲线是注水开发预测油藏动态的一个主要的方法。自1959年水驱特征曲线提出以来,很多学者对其进行了深入的研究,也取得了很多成果,目前主要集中在水驱曲线的理论基础、适用条件以及提高其精度的方法研究上 [1] - [8] 。在适用性以及应用方面,水驱曲线应用范围较广,比较常见的是用于预测可采储量及采收率,预测含水率、含水上升率、累产水量等开发指标以及计算动态地质储量 [9] ;此外,水驱曲线还可用于计算动态相渗,分析递减规律,分析剩余油等诸多方面 [10] [11] [12] ,但需要注意的时水驱曲线是有一定的适用性的,尤其是在低含水和特高含水阶段适应性差,同时不同的水驱曲线适用于不同的含水阶段、不同的原油粘度 [13] 。一般,水驱曲线适用于相对均质的油藏,但目前投入开发的很多油藏是非均质油藏,尤其是纵向极差较大的油藏,动态上表现出了明显的多层特征,对于复杂多层油藏而言,水驱曲线的适应性有待进一步考证。但目前很少有学者探讨水驱曲线在复杂多层油藏中的适应性;本文旨在解决水驱曲线在复杂多层油藏的适用方法,以进一步提高水驱曲线的应用范围及广度,同时为提高水驱曲线在复杂多层油藏预测精度提供一种思路和方法。
2. 水驱曲线理论基础分析
目前水驱曲线表达式较多,前期水驱曲线的提出基于统计学理论,但根据后期很多学者的研究结论表明 [1] [2] [4] ,大部分水驱曲线具有一定的理论基础,基于物质守恒方程以及相对渗透率模型。张金庆、陈元千、俞启泰等学者 [1] [4] [5] 在其著作中进行了总结。其基本推导过程如下:
基于不同的相渗曲线表达函数形式 [14]
(1)
(2)
(3)
(4)
(5)
基于物质平衡方程
(6)
通过数学推导可以得出不同类型的水驱曲线。目前标准中常用的水驱曲线公式有如下几种 [5] [15] :
a) 水驱特征曲线公式1——纳札洛夫水驱曲线,推荐用于低粘(小于3 mPa∙s)层状油藏和碳酸盐岩底水驱油藏。其表达式为
(7)
b) 水驱特征曲线公式2——马克西莫夫–童宪章水驱曲线,推荐用于中粘(3~30 mPa∙s)层状油藏。其表达式为
(8)
c) 水驱特征曲线公式3——西帕切夫水驱曲线,推荐用于中粘(3~30 mPa∙s)层状油藏。其表达式为
(9)
d) 水驱特征曲线公式4——沙卓诺夫水驱曲线,推荐用于高粘(大于30 mPa∙s)层状油藏。其表达式为
(10)
e) 水驱特征曲线公式5——张金庆水驱曲线,适用于任何原油粘度和类型的水驱油藏。其表达式为
(11)
f) 水驱特征曲线公式6——俞启泰水驱曲线,适用于任何原油粘度和类型的水驱油藏。其表达式为
(12)
通过上述理论推导过程探讨及常用水驱曲线表达式分析,得出如下认识:
1) 水驱曲线寻求的是动态指标的直线关系,以在应用时更加方便快捷;
2) 水驱曲线的理论基础是物质平衡方程和相渗曲线表达式;
3) 水驱曲线一般有一定的适用条件如油水粘度比等,同时需出现直线段,一般需到中高含水期。
3. 复杂多层油藏水驱曲线适应性分析
通过水驱曲线理论推导可以看出,水驱曲线的表达式系数隐含了物性参数、相渗曲线参数、地质储量以及流体参数,那么对于强非均质多层油藏,不同层地质储量不同,且其物性参数及相渗曲线参数不同,可不可以直接拟合预测呢?
3.1. 双层油藏中常用的六类水驱曲线
以两层为例,对于非均质油藏,不同的层系数a和b肯定不同,而且液量比例和油量比例也不同。
基于公式(7),两层水驱特征曲线记为
,
(13)
则
(14)
同理,基于公式(8)、(9)、(10)、(11)和(12),当两层时水驱特征曲线可以写为
 (15)
(15)
(16)
(17)
(18)
(19)
上述公式(13)到公式(19)均不能线性叠加,从数学的角度来看,直接用水驱曲线拟合预测不合理,其结果必然误差较大。
3.2. 双层油藏水驱曲线可以叠加的特例
如果在一定时期内,两层液量基本不变,且比例已知,则
,当一层见水,另一层未见水时,对于未见水层有
,
。
对于上述情况适当简化可进行叠加应用,以适用于任何原油粘度和类型的张金庆水驱曲线为例,双层的水驱特征曲线为
(20)
简化后为
(21)
但是当两层均见水后,则难以进行简化,需对产量进行劈分后预测,再叠加。可对曲线拐点分析,作为劈分依据。
本文通过分析,指出多层复杂油藏不能应用水驱曲线直接拟合预测,为解决复杂多层油藏中水驱曲线适应性,给出如下解决方案:首先基于地质认识(测井、沉积、岩心资料等)分析是否有必要分层;复杂多层油藏需分层、分阶段预测,最后叠加。
4. 复杂多层油藏多层动态特征及数模验证
为了证实上述复杂多层油藏水驱特征曲线预测解决方法,建立了数模机理模型。该模型采用1采1注,井距600 m,注采平衡。同时,为了方便研究,选择两层的纵向非均质模型(渗透率极差为2),其基本参数见表1,从表1可以看出,纵向渗透率不同的两层,其初始含油饱和度和残余油下水相相渗端点也有所不同。
在上述基础参数情况下进行模拟得到累产曲线,以甲型水驱特征曲线为例分析模拟结果,见图1,从图中可以看出,在B层见水前后,ln(Wp)~Np曲线呈现不同的趋势,当采用B层见水前曲线的趋势预测含水98%可采时,可采储量为2.75 × 104 m3,而当采用B层见水后的曲线趋势预测时,可采储量为2.33 × 104 m3,从最终的数模结果上可以明显看出,前者明显被高估,而后者非常接近数模的预测值2.32 × 104 m3。这是因为模型相对均质以及稀油导致水突破后两层的含水均急速上升,水驱特征曲线的拟合段的含水已经很高,所以用B层见水后的累产数据预测结果也可接受。但是实际上,模型还是比较理想化的,实际的含水受到多种因素的影响,含水很少出现急速上升的情况,此时若用第二层刚刚见水后的水驱特征曲线去预测最终可采也将存在较大的误差。更好的做法是分层分阶段进行预测,下面详细介绍。
分层分阶段预测时,需要根据PLT、历史拟合或者可靠的地层系数比值对产量进行劈分,将累产数据劈分到层后再进行叠加。为了验证分层分段预测的合理性,继续采用机理模型的模拟结果,对A层和B层分别应用甲型水驱特征曲线进行预测可采储量,详见图2和图3,预测出含水98%时A层和B层的可采分别为0.98 × 104 m3和1.31 × 104 m3,与模型预测的结果基本一致,验证了本文提出的方法是可靠的。
5. 复杂多层油藏水驱曲线预测实例分析
中东X油田是碳酸盐岩油藏,纵向非均质性强,是典型的复杂多层油藏。纵向上储层分为两段A段和B段,A段以白云岩为主,B段以灰岩为主,进一步细分为7个油组,分别为A1、A2、A3、B1、B2、

Table 1. Basic parameters of mechanism simulation model
表1. 机理模型基础参数表
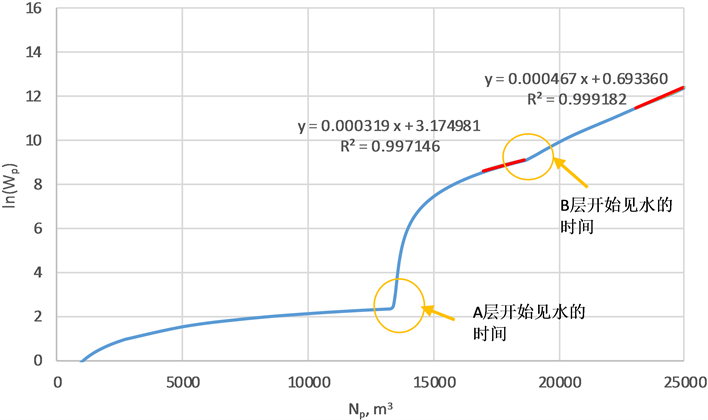
Figure 1. First type water flooding curve analysis of simulation results from mechanism model
图1. 机理模型模拟结果的甲型水驱特征曲线分析

Figure 2. First type water flooding curve of layer A after cumulative production split
图2. 累产量劈分后的A层甲型水驱曲线

Figure 3. First type water flooding curve of layer B after cumulative production split
图3. 累产量劈分后的B层甲型水驱曲线
B3和B4,各油组之间物性差异较大,详见图4,从图中可以看出,该油藏渗透率极差为35,纵向非均质性较强。
为了进一步分析复杂多层油藏水驱曲线的特征,以及在应用时存在的问题,选取一口典型井进行分析,该井的甲型水驱特征曲线,见图5,从图中可以看出,该井的动态特征出现了复杂多层特征。而且分析后,可以得到:1) 仅第一层见水其他层未见水时,未见水层累产油在增加,但产水量不增加,导致整体拟合预测会偏乐观,根据图中拐点前的趋势预测可采储量将达到23.4 × 104 m3;2) 第二层见水后,整体拟合预测时,不同的层处于不同的含水阶段,低含水阶段的层的动态特征将会影响整体的判断,根据图5的趋势,此时预测的可采仅6.0 × 104 m3,与前述预测值相差非常大;3) 根据本文提出的分层分阶段的方法进行预测,可以有效的解决上述的矛盾,得到的结果也更合理;4) 在分层分阶段预测可采储量时建议利用曲线的拐点校正劈分数据。
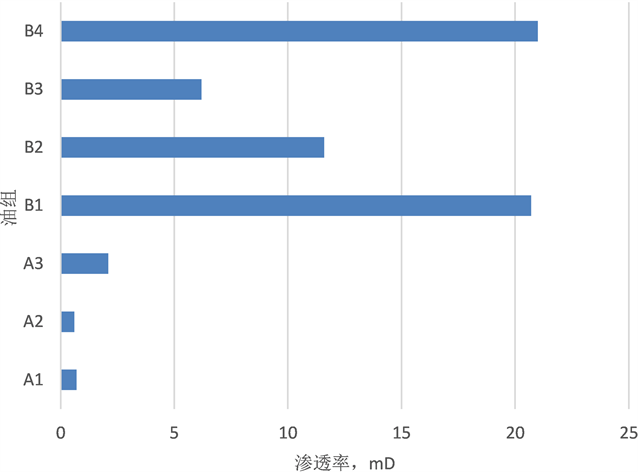
Figure 4. Well log permeability in all oil zone of X oilfield in Middle East
图4. 中东X油田各油组测井解释渗透率

Figure 5. First type water flooding curve of typical well with multi-layer commingle production of X oilfield in Middle East
图5. 中东X油田典型井多层合采甲型水驱特征曲线
6. 结论
1) 水驱曲线的理论基础是相渗曲线表达式及物质平衡方程。水驱曲线的系数隐含着不同的物性参数、不同的相渗参数以及不同的流体参数,本文探讨了其在纵向强非均质复杂多层油藏适用性,指出利用水驱曲线直接进行拟合预测误差较大;
2) 本文给出了复杂多层油藏水驱曲线的方法,其核心思想是分层、分阶段预测再叠加,通过数值模拟和敏感性方案分析,本文的提出方法可以一定程度上拓宽水驱曲线的实用性,对于复杂多层油藏指标预测具有一定的参考意义。
基金项目
中国海洋石油总公司创新基金[CNOOC-KY-KJCX-CRI-2017-01]。