1. 研究背景
在长距离输水管道和水电站输水管道等有压管道之中,会发生由于边界条件的突然改变(如阀门的突然启闭、机组的快速启动和断电甩负荷、管道突然堵塞等)引起管道内液体流速发生剧烈变化,从而导致液体内部压力急剧升高或者下降的现象,即发生水锤 [1] [2] 。这种压力的变化幅值非常高,其压力升高值甚至可以达到正常工作压力的几十倍甚至数百倍,同时也会产生极端负压。如此大的正压和负压值远远超过了材料的设计标准,极有可能引发爆管、机组抬机等事故,从而危害工程安全 [3] [4] [5] 。长久以来,对水锤波模拟的主要方法都是特征线法(Method of Characteristics,简称MOC)和有限体积法等方法,这是因为一维和二维的计算方法具有许多不容忽视的优点,其中最重要的一点就是计算速度快。随着计算机性能的不断提高,相关流体计算软件不断完善,并且相关的研究已经进入到一个更加成熟、更加精细化的层次之中,通过建立三维模型来模拟水锤已经具备相关基础。在一维模型计算时,常引入必要的简化(如:物理参数沿径向方向保持一致,等),这些理想化的简化虽然有利于推动计算的进行,但是简化后的模型和实际情况相比会有较大差异 [6] [7] [8] 。相对上述方法,三维建模和计算条件设置更加贴近实际情况,通过计算得出的数值模拟结果也有更直观、更多样的呈现方式 [9] [10] 。
本文依托三维CFD流体计算软件,通过分别模拟盲端和不同关闭时间的球阀,试图再现实验中球阀瞬时关阀所产生的直接水锤,找到影响实验结果的主要因素,同时分析球阀和与之相邻管道中液体的流态。
2. 物理模型
文中作为对比的实验数据是由Simpson和Bergant在1991年所做的实验所得,其实验装置的基本参数如下 [11] :管道总长37.2 m,下游布置盲端或者球阀,管道内径22 mm,恒定流水头差32 m,稳态流速0.3 m/s,管壁摩阻系数f = 0.034,初始雷诺数Re = 5600,水锤波波速c = 1319 m/s。实验装置示意图如图1所示。依据上述参数进行三维建模模拟。同时,作为对比的一维计算结果是由MOC计算所得。
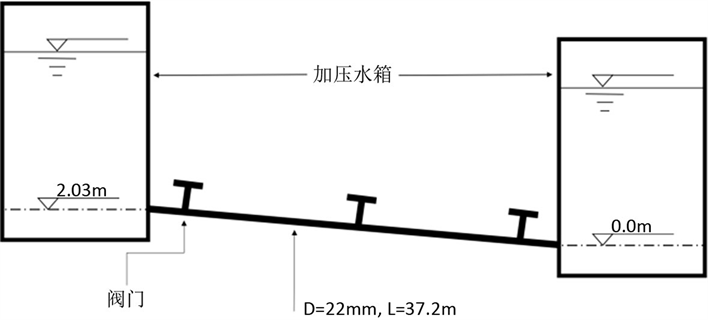
Figure 1. Schematic diagram of experimental set-up
图1. 实验装置示意图
3. 数学模型
3.1. 控制方程
1) 三维动量和连续性方程
本文三维模拟由于没有考虑流体温度的影响,所以流体计算方程是由连续性方程和动量方程两部分构成。
连续性方程:
(1)
式中:ρ为水体密度,1000 kg/m³;t为时间,s;ux,uy,uz分别为瞬时速度u在x,y,z方向上的分量,m/s;Sm为质量附加项。(变量用斜体)
动量方程:
在惯性参考系下,i方向的动量方程为:
(2)
式中:ρ为水体密度,1000 kg/m³;t为时间,s;P为压力,pa;gi为i方向重力加速度,m/s2;μ为黏性系数,N∙s/m2;Fi为外加作用力,N。
由于本次三维模拟需要考虑水体可压缩性,所以连续性方程和动量方程之中的ρ不可以作为定值来简化方程。
这里用的是球阀开启过程的瞬态数值模拟与实验研究。
2) 湍流模型
在此次三维数值模拟中采用的湍流模型为SST k-ω模型,这个模型是在k-ε模型和k-ω模型的基础上改进而来。SST k-ω模型由Menter提出,核心思想是近壁面利用k-ω模型的鲁棒性,以捕捉到粘性底层的流动;而在主流区域利用k-ε模型又可以避免k-ω模型对入口湍动参数过于敏感的劣势 [12] 。
其输运方程为:
(3)
(4)
式中:Gk为层流速度梯度产生的湍流动能;Gω为ω方程产生的湍流动能;Γk和Γω为k方程和ω方程的扩散率;Yk和Yω为由扩散产生的湍流 [13] [14] 。
3) 液体状态方程
在本次三维数值模拟中需要考虑液体的可压缩性,在这里是通过添加液体状态方程—泰特方程来实现的。
泰特方程:
(5)
(6)
(7)
式中:n为根据经验所取常数;ρl,0为液体初始密度,kg/m³;pl,0*为操作压力,pa;
;a为水锤波波速,m/s。
3.2. 模型求解
本文采用的求解器为分离式求解器,即Pressure based Solver;采用的算法为SIMPLE,其计算方式分两步走,即先预测再修正;采用的离散方法为一阶迎风格式,即First order upwind,其考虑了流动方向,可以得到物理上合理的解。
3.3. 几何模型和边界条件
本次三维模拟所有部件均采用结构化网格,通过多次对比,本次模拟确定采用的网格数量分别如下:下游为盲端时,网格总量为6.25万;下游为球阀时,网格总量为6.255万。网格划分采用O型网格,这种网格划分方法相对其他方法来说更加贴近实际,模拟效果也更好。计算软件采用三维流体计算软件,其中球阀的运动是通过编写程序来控制网格的移动来实现的,这种方式也与实际情况相一致;水体的可压缩性也是通过编写程序来实现的。计算时开启能量方程,湍流模型采用SST k-ω模型,管中为单相流即只有水。首先用稳态计算使流场稳定,同时各项参数(压力、流速和流量等)与实验所测值相一致,之后将计算结果作为初始流场,开始非恒定流的计算。上游边界条件为压力进口,下游边界条件为压力出口 [15] 。
4. 三维计算结果
4.1. 模型验证
本文将已有实验数据与数值模拟结果进行对比分析。如图2所示,数值模拟结果包括一维、三维两种结果。对比结果见图2。结果显示,三维计算结果(压力峰值、波动周期)与实验压力波动曲线更为接近,即,三维模拟结果比一维更为准确。
虽然三维计算结果与实验结果吻合较好,但后期的压力波动周期中,三维计算所得压力周期与实验值略有差异,可能的原因:三维计算所采用阀门边界可能与实际情况有所差别。接下来,本文将分析研究阀门形状、关闭时间对瞬变压力的影响。
4.2. 阀门形状对直接水锤的影响
首先考虑两种不同的阀门形状,主要是通过三维计算将结果与实验结果对比来考察阀门形状对直接水锤压力的影响。对比结果如图3。由于盲端和球阀是两种不同的结构,其挡水面的形状是不同的,如图3所示。计算结果如图4,由图4中可以发现,阀门为平面和球面所得结果之间差别很小,周期方面吻合程度很高,两条曲线基本重叠,主要的差别集中在峰谷值处。由于差别非常小,可以认为这种差别不会对数值模拟产生影响。再将这两条曲线和实验数据进行对比,我们发现即使采用了相当于0 s关闭球阀的球面,其结果在表示时间的横轴方向上与实验数据仍然存在较大差异,这个差值大约在0.008~0.015 s左右。根据我们的数值模拟所得结果,两种不同的阀门形状只是对峰谷值产生了很小的影响,而并没有使水锤产生时间和水锤周期产生任何影响,这从图3中有很明显的体现,所以可以肯定造成这种差异的原因并不是阀门处的形状。
这组数据对比证明阀门的形状对水锤波的压力峰谷值只会产生极小的影响,并且证明了阀门的形状并不是造成三维数值模拟结果与实验结果在时间上有差别的原因。
4.3. 阀门关闭时间对直接水锤的影响
在排除了阀门形状的影响之后,开始研究关阀时间的影响,在此考虑了3种不同的关阀时间,以期更全面的分析其对直接水锤的影响。计算结果如图5,在这组实验中,采用了3种不同的关阀时间。之
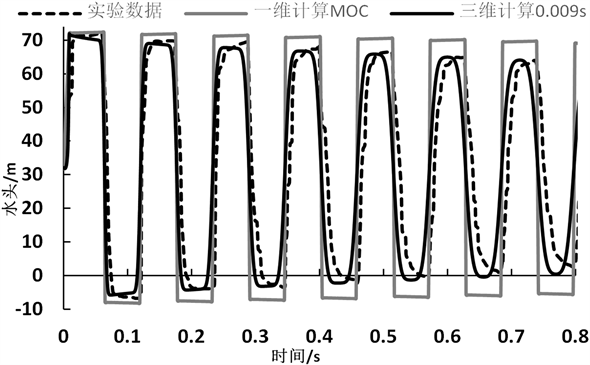
Figure 2. Comparative analysis of 3D, 1D and experiment
图2. 一维、三维计算结果和实验数据对比
 (a)
(a)  (b)
(b)
Figure 3. Schematic plots for different shape of valve: (a) Plane; (b) Sphere
图3. 不同阀门形状示意图:(a) 阀门处为平面;(b) 阀门处为球面
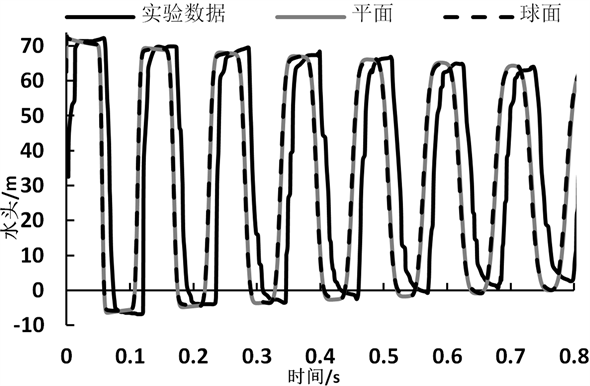
Figure 4. Comparative analysis of the results between different shape of valve and experiment
图4. 不同阀门形状所得计算结果与实验数据对比
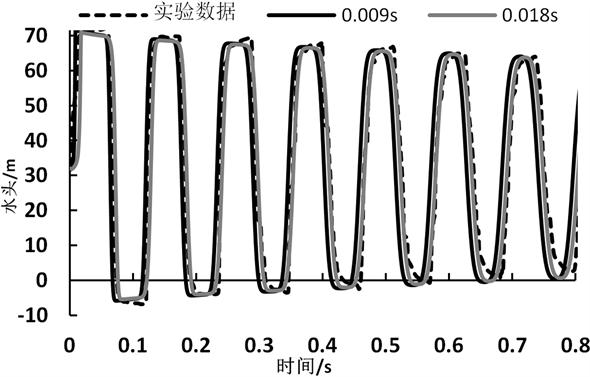
Figure 5. Comparative analysis of the results between different closing time and experiment
图5. 不同关阀时间所得计算结果与实验数据对比
所以采用这两种关阀时间是因为:
1) 0 s关闭的球阀是一组附加的参考对比值,采用0 s关阀相对于采用盲端作为对比更具有代表性,也可以排除一些不必要的干扰,从而使对比具有更高的可信度。
2) 0.009 s的球阀关闭时间是实验中采用的关阀时间,这种关阀时间在最大程度上保持了与实验的一致性,这组数值模拟对实验的还原度最高,所以具有很高的参考价值。
3) 0.018 s的球阀关闭时间也是一组附加的参考对比值,因为之前的数值模拟数据和实验数据的对比过程中,发现数值模拟数据在时间上总是与实验数据有较大差异,这种差异有两点很明显的表现:第一点是水锤波的产生时间比实验测得要早,第二点是水锤波的周期2 L/a会随着时间增长。所以我们尝试将关阀时间延长,以期得到与实验数据比较接近的数值模拟结果。
通过对比可以发现,相对于0 s和0.009 s模拟结果来说,0.018 s的数值模拟结果反而与实验结果在时间上更为贴近。经过仔细的对比,可以发现作为基准的0.009 s关闭球阀其数值模拟结果是符合理论解的,即水锤波的峰值开始产生的时间为0.009 s,每个水锤波的周期为:
将图5局部放大,可以得到图6和图7,从这两张图我们可以看到,实验数据中水锤波达到峰值的时间是0.0136 s,也就是说实验中关阀时间并不是0.009 s,或者是测量方式没有达到相应精度。这就造成实验所得结果会整体向右移动0.0136 s。也就是如图6中所示的情况。再来看关阀时间为0.018 s时的数值模拟结果。在图7中,我们可以看到在这种情况下水锤波达到压力峰值的时间是0.018 s,比标准关阀时间0.009 s要慢0.009 s,所以相应的其结果会整体向右移动0.009 s,这样其结果所绘曲线与实验结果所绘曲线之间在时间上的差别相较于0.009 s这种情况所绘曲线就要小得多。
这组数据对比的主要目的是说明球阀关闭时间为0.009 s时,三维数值模拟结果虽然和实验数据仍有差异,但其结果已经可以满足精度要求,并且具有指导意义,如果将其作为几个基准值,有利于加深对实验数据的进一步深入分析研究。

Figure 8. Velocity field of fluid during the ball valve is closing
图8. 球阀关闭过程中流体内部速度场
4.4. 三维流场
通过上面几组数据的对比,可以发现三维数值模拟结果是可靠的。由于球阀快速关闭,球阀内部和与之相邻的管道中的液体流态十分复杂,流场的变换也非常剧烈,通过三维数值模拟,可以将其直观、形象的呈现出来,这是三维数值模拟的一个优势,也是一维数值模拟所不具备的。
图8是关阀时间为0.009 s时球阀内部和与之相邻管道中的液体的速度场云图,从中可以发现在球阀关闭过程中,由于关闭速度很快,所以速度场受关闭速度影响较大。
5. 结论
本文主要研究了有压管道中因球阀关闭引起的直接水锤。基于计算流体力学通用软件,通过引入水体可压缩性的源相,实现了对产生三维直接水锤环境的建模,并且成功的模拟了三维直接水锤的产生和发展。利用已有实验结果验证了所建三维模型可以准确模拟球阀关闭过程中的水锤压力波动。与现有的一维计算模型相比,三维模型不仅能够模拟出更为精确地压力变化,并且能直观地再现发生直接水锤过程中液体内部的三维流场。
同时,进一步分析了阀门处形状和阀门关闭时间对三维数值模拟结果的影响。从计算结果的对比之中可以看出,阀门形状变化对于直接水锤模拟影响很小;关阀时间对瞬变压力影响显著。
基金项目
国家电网公司科技项目资助(合同号:SGBXSJJS1700007)。