摘要: 本文基于密度泛函理论的第一性原理方法,在广义梯度近似下,研究了硅碳纳米管(8, 0)几何结构和电子结构性质。硅碳纳米管(8, 0)是由32个碳原子和32个硅原子,共计64个原子组成的折叠之字形结构。计算结果表明:硅碳纳米管(8, 0)的相邻原子碳和硅所构成的Si-C键的平均键长为0.1787 nm,平均直径为0.797 nm。对电子结构性质的研究是通过将最高占据轨道和最低未占据轨道的能隙进行了分析,实验中得到能带最高占据轨道跟最低未占据轨道为1.344 eV,并且其能带最高占据轨道跟最低未占据轨道在同一对称点上,因此定性其为直接带隙半导体。通过对硅碳纳米管(8, 0)电子态密度图分析,发现其电子分布的峰值差异较大:电子主要分布在−0.55 eV~0.15 eV之间,其中−0.35 eV~0.3 eV和0.12 eV~0.15 eV之间几乎无电子分布,在−0.15 eV~−0.12 eV之间电子分布最多。通过本计算模拟研究可对今后硅碳纳米管的结构、性能研究及应用发展提供理论参考。
Abstract:
In this paper, based on the first principle method of density functional theory, the geometric structure and electronic structure properties of silicon carbon nanotubes (8, 0) are studied under the generalized gradient approximation. Silicon carbon nanotube (8, 0) is a folded structure con-sisting of 32 carbons and 32 silicon atoms, which consist of 64 atoms. The calculated results show that the average bond length of the Si-C bond formed by the adjacent atoms carbon and silicon of silicon carbon nanotubes (8, 0) is 0.1787 nm, and the average diameter is 0.797 nm. The study of the properties of electronic structures is based on the analysis of the energy gap of the highest oc-cupying orbit and the lowest unoccupied orbit. In the experiment, the maximum occupying orbit and the lowest unoccupied orbit are 1.344 eV, and the highest occupying orbit and the lowest un-occupied orbit are at the same symmetry point, so it is qualitatively the direct band gap Semicon-ductor. By analyzing the electron density map of silicon carbon nanotubes (8, 0), it is found that the electron distribution peaks are different: electrons are mainly distributed between −0.55 eV and 0.15 eV, of which there is almost no electron distribution between −0.35 eV to 0.3 eV and 0.12 eV to 0.15 eV, and the most electron distribution is between −0.15 eV and −0.12 eV. The present study will provide theoretical references for the future research and application of silicon nanotubes.
1. 引言
1991年,日本学者Ijima [1] 在观察石墨电弧产物中,意外发现了由管状的同轴纳米管组成的碳分子,即碳纳米管,一种全新超级材料问世了。随着碳纳米管及纳米材料的深入研究,该材料所展现良好的力学、磁学、电学、化学性能极具广泛应用前景 [2] [3] [4] 。碳纳米管具有以下几种优异的性能:一是碳纳米管具有良好的热传导性能,可以合成高各向异性的热传导材料。另外,碳纳米管有着较高的热导率,在复合材料中掺杂微量的碳纳米管,将会很大可能改善该复合材料的热导率。二是碳纳米管可以被看成具有良好导电性能的一维量子导线。正因为碳纳米管的结构与石墨的片层结构相同,所以具有很好的电学性能。理论预测其导电性能取决于其管径和管壁的螺旋角。三是碳纳米管为纳米级结构,缺陷很少,故使碳纳米管具有高模量、高强度、优异的力学性能。总而言之正是由于碳纳米管独特的结构,使其具有良好的电学性能和力学性能以及化学性能。在电子学领域、材料工程领域、环境监测以及医学检测等方面都有着广泛应用。在实际应用当中,大量的理论以及实验研究指向如何采用各种不同的方法对其电子结构特性进行调控 [5] [6] 。
近年来科研人员发现对碳纳米管进行掺杂、取代和修饰以后,其功能和应用范围将会得到大大的提高。其中掺杂主要有两种方式:一种是将杂质原子修饰碳纳米管表面;另一种是将杂质原子嵌入碳纳米管骨架中。尽管实验研究已取得长足进展,但理论研究还处于薄弱环节,且大多集中于掺杂对硅纳米管结构和性质的影响 [7] [8] 。Zhang等 [9] 用密度泛函理论计算研究发现硼掺杂的碳纳米管能够很灵敏检测出氰化物,为碳纳米管氰化物传感器的研究奠定基础。诸多实验和理论研究都表明,对碳纳米管进行掺杂有效提高了碳纳米管气体传感器的检测灵敏性和选择性,扩展了检测范围。
2001年首次合成的硅碳纳米管,其侧壁折叠结构使外表面的化学反应活性强且具有较好的热稳定性。就目前各方面性质性能上来看更优于碳纳米管。因此对于深入研究硅碳纳米管的合成机理和性能颇具现实意义。本文基于密度泛函理论的第一性原理方法,对硅碳纳米管(8, 0)几何结构和电子结构进行研究 [10] ,为探索硅碳纳米管的结构、性能及应用发展提供了理论参考。
2. 计算方法及过程
基于密度泛函理论(DFT)的第一性原理计算方法,通过在DMol3软件包中实现电子自旋极化的计算,对之字形硅碳纳米管(8, 0)的基态结构和电子结构性质进行模拟研究。其结构优化和相应的稳定几何结构的总能量计算是基于用J. P. Perdew等 [11] 人修正的广义梯度近似(generalized gradient approximation, GGA)。采用全电子计算结合双数值基矢考虑极化函数(DNP)。通过Monkhorst-Pack方案在布里渊区网格自动产生的不可约k点进行自治计算。对于所有模型将k点设置为1 × 1 × 5,将能量收敛标准设定为2 × 10−6 a.u.、体系最大受力的收敛标准设定为0.001 Ha/Å以及自洽计算能量收敛标准设定为10−6 a.u.。
3. 计算结果及分析
通过模拟硅碳纳米管(8, 0)的基态结构,清楚的显示了不同视角下的硅碳纳米管(8, 0)的几何结构,如图1(a)和图1(b)所示。其中(a)为硅碳纳米管(8, 0)的俯视图,(b)为硅碳纳米管(8, 0)的主视图。可观察图中共有64个原子,其中碳原子有32个(灰色),硅原子有32个(黄色)。并且发现,硅原子和碳原子并不在同一平面上。其经过结构优化后的,发现之字形硅碳纳米管(8, 0),类似于氮化硼纳米管,电负性原子(C原子)几乎全都向外移动,更多的阳性(Si原子)向内移动,形成了波纹状的表面。这也是造成碳纳米管和硅碳纳米管形貌的差异原因之一,碳纳米管的表面相对光滑,而硅碳纳米管表面出现了折叠结构。根据Xiao Wang等 [12] 人报告数值显示,Si-C平均键长为1.787 Å,Si-C平均直径约为7.97 Å。此次计算Si-C键的平均键长为0.1787 nm,平均直径为0.797 nm与以前报告的值吻合程度高。导体、半导体、绝缘体的不同,主要是能带结构不同。作为半导体材料的硅碳纳米管(8, 0)是存在能带能隙,在整个研究过程中我们得到了如图2所示的能带图。通过分析能带可以更进一步了解其电子结构性质。根据能带理论,电子主要分布在满价带,当半导体受到温度影响时,满价带的电子就会激发到导带上,在价带上留下空轨道即空穴。温度越高,电子被激发到空导带的概率越大。导带上电子和价带上的空穴决定了半导体的导电能力。通过实验得到的数据,其能带最高占据轨道跟最低未占据轨道为1.344 eV,并且其能带最高占据轨道跟最低未占据轨道在同一条直线上。通过不同的两种跃迁方式:竖直跃迁和非竖直跃迁可将半导体分为直接带隙半导体和间接带隙半导体。因此硅碳纳米管(8, 0)是一种直接半导体材料而不是间接半导体材料。而对比以前的实验数据显示其能带最高占据轨道跟最低未占据轨道为1.344 eV。同时,能带最高占据轨道跟最低未占据轨道都出现在G点处。
为了进一步了解之字形硅碳纳米管(8, 0),我们将会从电子态密度总能带来分析之字形硅碳纳米管(8, 0),如图3为之字形硅碳纳米管(8, 0)的电子态密度图。图中纵坐标DOS为电子态密度,横坐标E为能量,由图观察发现,电子主要分布在−0.55 eV~0.15 eV之间,其中−0.35 eV~0.3 eV和0.12 eV~0.15 eV之间几乎无电子分布,在−0.15 eV~−0.12 eV之间电子分布最多,并发现电子分布的峰值差异较大,这是由每个硅原子所处位置的不同对称性所导致的。
4. 结语
采用基于密度泛函理论的第一性原理方法研究了硅碳纳米管(8, 0)的基态结构和电子结构性质。硅碳纳米管(8, 0)是由32个碳原子和32个硅原子,共64个原子组成的折叠之字形结构。计算结果表明,硅碳
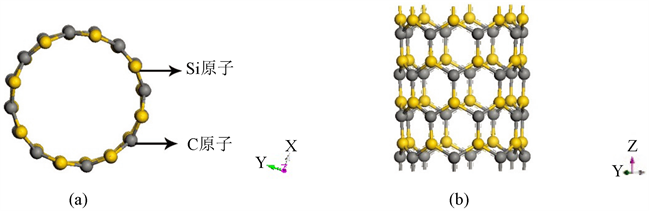
Figure 1. Schematic diagram of geometric structure
图1. 硅碳纳米管(8, 0)的几何结构示意图

Figure 3. Energy density graph
图3. 硅碳纳米管(8, 0)的电子态密度图
纳米管相邻原子Si-C键的平均键长为0.1787 nm,平均直径为0.797 nm;对于电子结构性质的研究发现其与结构的手性相关,通过其能带最高占据轨道跟最低未占据轨道为1.344 eV,并且其能带最高占据轨道跟最低未占据轨道在同一条直线上,其为直接带隙半导体。从电子态密度图来看电子分布的峰值差异较大,电子主要分布在−0.55 eV~0.15 eV之间,其中−0.35 eV~0.3 eV和0.12 eV~0.15 eV之间几乎无电子分布,在−0.15 eV~−0.12 eV之间电子分布最多。
致谢
本研究受到新疆大学2017年度自治区级大学生创新训练计划项目(No: 201710755049)以及新疆维吾尔自治区自然科学基金项目(No: 2016D01C065)资助。
NOTES
*通讯作者。