1. 引言
层状岩体在自然界中分布十分广泛,由于其存在着一组优势贯穿结构面,与完整岩石相比,其结构面上的抗剪强度较低,易发生倾倒、弯折以及离层等变形破坏 [1] [2] [3] [4] [5] 。求解上述层状岩体力学问题时,一般可将岩体简化为岩梁进行分析计算。目前,大部分学者针对均质梁分析较多,而对于非均质梁的研究主要集中在层间无滑动的组合梁方面。梁运培等 [6] 提出了采场上覆岩层移动的组合模型,对组合岩梁模型在岩层移动规律研究及地表沉降控制方面进行了深入分析。黄菊华等 [7] 讨论了不同叠合方式的叠合梁的应力分析问题,得出不同材料、不同叠合方式对应力的影响规律。徐铎等 [8] 对岩梁材料拉压弹性模量不尽相同的横向叠加组合岩梁分层截面应力大小分布情况作了分析。而分析层间有滑动的叠合梁方面,运用数值计算的方法研究时一般需要到层间接触刚度参数,即剪切刚度和法向刚度 [9] [10] 。而目前在鲜有文献讨论接触刚度参数对叠合梁应力分布的影响规律,鉴于此,本文以两端固定叠合岩梁为例,运用FLAC3D数值计算软件,建立叠合岩梁在均布外荷载作用下的不同接触刚度参数时的应力求解模型。研究成果可为争取选取接触刚度参数提供一定的借鉴与参考。
2. 层面的变形性质
在不同地质作用中,岩体中形成了不同的结构面,比如层理、岩层面、不整合面和软弱夹层。在荷载作用下,岩体中的应力分布受结构面及其性质的影响 [11] 。在此主要研究岩层之间的接触面即层面的变形性质对应力分布的影响。
2.2. 法向变形性质
当结构面法向力
为压应力时,结构面产生法向压缩变形。开始先为点或线接触,经挤压,局部破碎或劈裂,接触面增加。结构面压缩量呈指数曲线特征 [12] [13] ,其指数函数为:
(1)
式(1)中u为结构面法向压缩量,cm;u0为法向压应力,Mpa;Kn为结构面法向刚度,Mpa/cm。
法向刚度Kn是反映结构面法向变形性质的重要参数。其定义为在法向应力作用下,结构面产生单位法向变形所需要的应力,数值上等于法向变形曲线上的一点的切线斜率,即:
(2)
2.2. 剪切变形性质
在一定的法向压应力作用下,结构面在剪应力作用下产生沿层面方向的滑移形成层间剪切带。结构面在剪力作用下产生塑型变形和脆性破坏。可用应力—变形曲线关系表征其变形规律,用剪切刚度Ks表示其变形性质,剪切刚度Ks是反映结构面剪切变形性质的重要参数 [11] 。剪切刚度Ks是剪切变形曲线斜率:
(3)
式(3)中Ks为结构面剪切刚度,MPa/cm。对于结构面的抗剪强度,可以用库伦—莫尔准则来表达:
(4)
式(4)中
为平行结构面的剪应力,MPa;
为垂直结构面的正应力;
为结构面内摩擦角,(˚);C为结构面的凝聚力,MPa。
3. 数值模型的建立
3.1. 模型概述
为寻找岩层层面接触刚度,即层面的剪切刚度和法向刚度对叠合岩层应力分布和位移的影响,采用弹性力学模型 [14] ,通过FLAC3D进行数值模拟。建立如图1所示模型,双层叠合固定梁由两层岩性不同的岩层上下自然叠合而成,叠合梁的两端为固定端,梁的跨度为l,上下层的高度分别为h1和h2,宽度b为1;两岩层的弹性模量为E1和E2,泊松比为v1,v2;梁表面受均布荷载q作用,上下岩层之间存在接触层面,接触面剪切刚度Ks/Mpa∙cm−1,法向刚度Kn/Mpa∙cm−1。
3.2. 参数的选取
计算模型中上层岩梁的弹性模量E1,泊松比v1;下层岩梁的弹性模量E2,泊松比v2。叠合梁的跨度l,梁的上表面承受的均布荷载q,上层高度h1,下层高度h2,梁的宽度b,参数取值见表1。在上、下层之间设置接触面,接触面初始剪切刚度Ks = 5 Mpa/cm,初始法向刚度Kn = 10 Mpa/cm。
当保持接触层面法向刚度Kn初始值不变时,改变层面剪切刚度Ks (Ks = 5 + 5i, I = 0~9),当保持接触层面剪切刚度Ks初始值不变时,改变层面法向刚度Kn(Kn = 10 + 10i, I = 0~9)。
3.3. 监测点的布置
Flac3d模拟中把模型分为240个单元体,监测单元体应力和位移,选取A、B两个单元体作为监测点,监测其水平方向应力和垂直方向应力,监测A和B单元体垂向位移。A单元体坐标为(x, y, z),(x = 15, 16; y = 0, 1; z = 2, 3),B单元体坐标为(x, y, z),(x = 15, 16; y = 0, 1; z = 6, 7),A、B单元体在叠合岩梁模型中位置如图2。

Figure 1. Analysis model of laminated rock beam
图1. 叠合岩梁分析模型

Table 1. Parameter value table for analysis model of laminated rock beam
表1. 叠合岩梁分析模型参数取值表

Figure 2. Location of monitoring points A and B
图2. 监测点A、B位置
4. 模拟结果分析
4.1. 应力分析
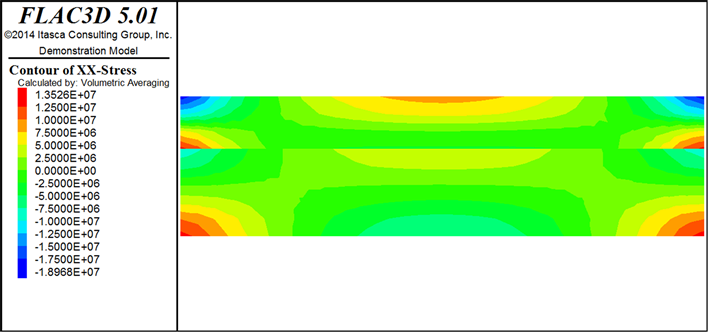
通过FLAC3D对初始条件下双层叠合岩梁的应力模拟,在接触面剪切刚度Ks = 5 Mpa/cm,法向刚度Kn = 10 Mpa/cm时,岩梁水平方向和垂直方向应力分布如图3(a)、图3(b)所示。在上覆均匀荷载q作用下,简支岩梁上、下层水平方向应力最大值集中在梁的两端,上下层的上缘和下缘分别处于受压和受拉状态,垂直方向应力由上到下分布,均匀减小,上层应力通过接触面传递到下层,通过接触面时由于接触面变形性质作用,传递到下层的应力减小。
1) 改变剪切刚度
当改变接触面剪切刚度Ks时,叠合岩梁应力分布发生变化,随着剪切刚度Ks的增大,岩梁上、下层两端应力向跨中集中,岩梁水平方向最大拉应力和最大压应力都减小,岩梁上、下层最大应力与剪切刚度Ks呈负相关;当剪切刚度Ks小于15 Mpa/cm时,岩梁垂直方向的最大应力随着Ks的增大而减小,当Ks大于15 Mpa/cm时,岩梁垂直方向的最大应力不变,如图4(a)、图4(b)所示。
叠合岩梁上层B单元体应力大于下层A单元体,岩梁上层跨中应力较集中,随着层面剪切刚度Ks的变化,单元体A和B的水平方向和垂直方向应力发生变化,如图5(a)、图5(b)所示。随着Ks的增大,单元体A的水平和垂直方向应力减小,当Ks大于15 Mpa/cm时,单元体A水平应力方向发生变化并随着Ks的继续增大而增大,垂直方向应力减小趋势变缓,当Ks大于30 Mpa/cm时垂直应力不变;单元体B的水平方向应力随着Ks的增大而增大,增速逐渐变缓,垂直方向应力增加,当Ks大于15 Mpa/cm时不变。
2) 改变法向刚度
当叠合岩梁层面剪切刚度Ks不变,改变法向刚度Kn时,叠合岩梁上、下层水平和垂直应力分布发
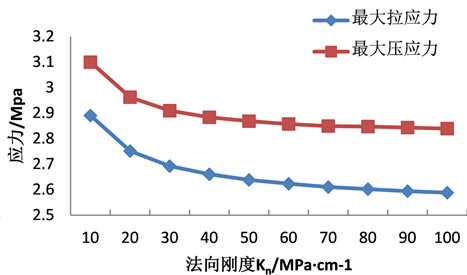
生变化,随着法向刚度Kn增大,叠合岩梁水平方向最大拉应力逐渐增加并趋于稳定达到14.15 Mpa,最大压应力逐渐减小到17.65 Mpa (图6(a)),其垂直方向最大拉应力和压应力均减小(图6(b)),当Kn大于30 Mpa/cm时,减速变缓。
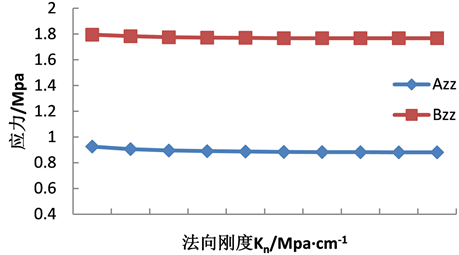
随着层面法向刚度Kn的增大,单元体A和B的水平和垂直方向应力发生轻微变化,如图7(a)、图7(b)
 (a)
(a)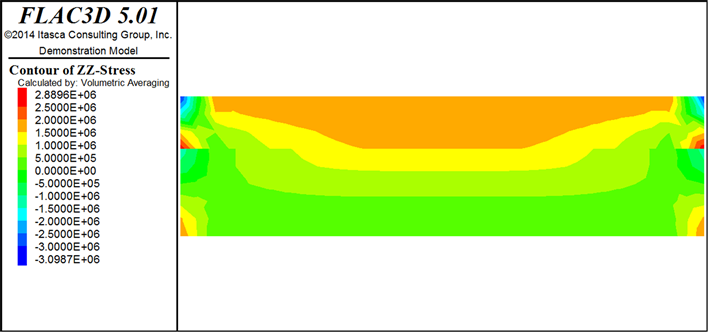 (b)
(b)
Figure 3. Stress distribution of laminated rock beams
图3. 叠合岩梁应力分布
 (a)
(a) 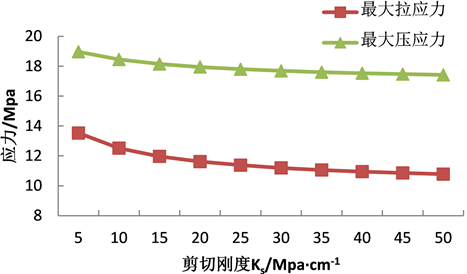 (b)
(b)
Figure 4. Maximum stress change of laminated rock beam
图4. 叠合岩梁最大应力变化
 (a) (b)
(a) (b)
Figure 5. Stress change of cell body A and B
图5. 单元体A、B应力变化
 (a)
(a) 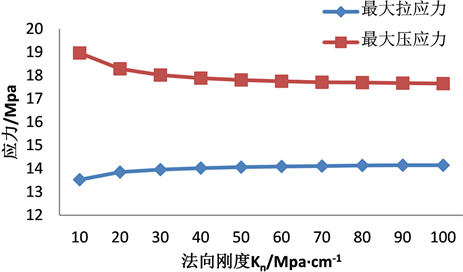 (b)
(b)
Figure 6. Maximum stress change of laminated rock beam
图6. 叠合岩梁最大应力变化
 (a)
(a)  (b)
(b)
Figure 7. Stress change of cell body A and B
图7. 单元体A、B应力变化
所示,随着Kn的增大,当Kn小于30 Mpa/cm时,单元体A的水平应力增大,垂直应力减小,当Kn大于30 Mpa/cm时,单元体A应力基本不变。随着Kn的增大,单元体B的应力基本不变。
4.2. 位移分析
由于叠合岩梁两端为固定端,所以岩梁两端没有垂直位移,岩梁垂直位移由跨中向两端均匀减小。在接触面初始剪切刚度Ks = 5 Mpa/cm,初始法向刚度Kn = 10 Mpa/cm的条件下,岩梁跨中最大垂直位移14.743 mm,如图8。由于上下层接触面接触刚度的作用,距垮中等距时上层位移大于下层位移。

Figure 8. Vertical displacement of laminated rock beams
图8. 叠合岩梁垂直方向位移
 (a)
(a) 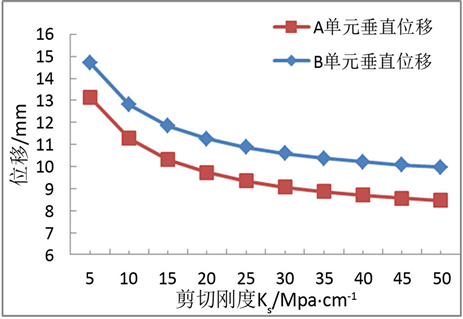 (b)
(b)
Figure 9. Vertical displacement of element A and B
图9. 单元体A、B垂直位移
A单元位于叠合岩梁下层,B单元位于岩梁上层,随着层面接触刚度的变化,在上覆均匀荷载作用下,岩梁垂直方向位移有较大变化,其水平方向位移忽略不计。
当保持法向刚度Kn不变,改变剪切刚度Ks,岩梁垂直位移变化如图9(a)所示。当剪切刚度Ks增大时,A单元和B单元的垂直位移都减小,A单元位移小于B单元。改变切向刚度Ks时,叠合岩梁上下层弯曲均减小。
当保持剪切刚度Ks不变,改变法向刚度Kn,岩梁垂直位移变化如图9(b)所示。当剪切刚度Kn增大时,A单元垂直位移增大,B单元垂直位移减小,A单元位移小于B单元。当Kn大于30 Mpa/cm时,A和B垂直位移增速和减速变缓。改变法向刚度Kn时,叠合岩梁上层弯曲减小,下层弯曲增加。
5. 结论
a) 双层叠合简支岩梁在上覆均匀荷载作用下,内部应力分布受中间层面接触刚度的影响,上层应力大于下层应力,上层应力通过接触面时减弱。层面变形性质包括层面的剪切刚度Ks和法向刚度Kn,二者的变化对于双层叠合岩梁内部应力分布有着很大的影响。
b) 当增加接触面剪切刚度Ks时,岩梁水平方向最大拉应力和最大压应力都减小,岩梁上、下层最大应力与剪切刚度Ks呈负相关;当剪切刚度Ks小于15 Mpa/cm时,岩梁垂直方向的最大应力随着Ks的增大而减小,反之则不变。随着剪切刚度Ks的增大,岩梁下层内部的水平和垂直方向应力减小,上层内部的应力增大。当Ks大于15 Mpa/cm时,岩梁内部应力变化趋势变缓直至趋于稳定值。
c) 当增加接触面法向刚度Kn时,叠合岩梁水平方向最大拉应力逐渐增加并趋于稳定达到14.15 Mpa,最大压应力逐渐减小到17.65 Mpa;其垂直方向最大拉应力和压应力均减小,当Kn大于30 Mpa/cm时,减速变缓。岩梁内部上、下层的水平和垂直方向应力发生轻微变化,当Kn小于30 Mpa/cm时,岩梁下层的水平应力增大,垂直应力减小,反之则基本不变。岩梁上层内部应力基本不变。
d) 岩梁垂直位移由跨中向两端均匀减小。由于上、下层接触面接触刚度的作用,距垮中等距时上层位移大于下层位移。当增加剪切刚度Ks时,岩梁上下层垂直位移都减小,下层位移小于上层。当增加法向刚度Kn,岩梁下层垂直位移增大,上层垂直位移减小,A单元位移小于B单元。当Kn大于30 Mpa/cm时,下层和上层垂直位移增速和减速变缓并趋于稳定。
基金项目
国家自然科学基金面上项目(51471008)。