1. 引言
金融行业在人们的日常生活中所占的比重在日益加重,越来越多金融研究人员及统计相关人员都致力于研究与股市相关的课题。与此同时,经济全球化、贸易全球化的影响也日益深远,另外货币与资本的流通也同样促使各股市间的联动性。因此该选题具有现实意义,通过相关文献的查找与阅读,可见大多数文献都未曾使用传递函数的方法针对国际间股市的相关性进行相关研究。但也能找到使用格兰杰因果检验及向量自回归模型证明联动的文献,因此可用协整检验、格兰杰因果检验及VAR模型验证国内上海证券交易所及纳斯达克证券交易所的联动性及建立相应模型。
2. 国内外研究现状综述
Tadaaki Komatsubara (2017) [1] 使用Three-Regime STC模型对1995年至2013年东亚地区的上海、香港、韩国及日本的债券交易所进行分析建模,得出在1995年各股市间的联动性还不甚明显,但从1995年到2003年间各股市间联动性上升很快。2003年后股市联动性维持在一定水平。
何苏燕(2016) [2] 使用平稳性证明,证明了深圳证券交易所的深证综指、上海证券交易所的上证综指、债券市场指数收益率均满足平稳性。接着该作者使用格兰杰因果检验观察几个综合指数收益率间的因果关系,并通过SVAR模型的构造建模。
裴延华、余万林(2017) [3] 在《基于沪港通前后沪港和沪美股市的联动性的比较分析》中,选取的上海证券综合指数、恒生指数和标准普尔500作为三个股市股价变化的代表变量,进行单位根检验后,对三个指数进行了协整检验,证明了他们之间的协整关系。之后对沪港通开通前后三个指数的一阶差分进行了格兰杰因果检验,证明开通前不存在明显的因果关系,开通后在0.1的显著水平下沪港股市存在因果关系,而其他股市间,因果关系不明显。该作者还进行了向量自回归模型的建模,证明沪港通开通后,上海股市的指数对恒生指数的方差分解值增大,即能够解释更多的恒生指数的变化。
西村友作(2009) [4] 选取上证综指和道琼综合指数作为代表变量,使用单位根检验证明两个指数为均为一阶单整序列,使用EGARCH模型,证明两个股市收益率均存在波动非平稳性。并使用CFF检验证明滞后一阶的美国股市与上海股市存在因果关系。
马千里(2015) [5] 使用VAR-MGARCH-BEEK模型分析股市及汇率间的波动溢出效应。
张兵、范致镇及李心丹(2010) [6] 在《中美股票市场的联动性研究》中,选取上证综指及道琼斯指数,为各股市代表数据,先证明这几组市间序列的单整阶数相同,再使用DCC模型分析他们的波动溢出效应,发现中国股市对美国股市的波动溢出效应一直不明显。但美国股市对中国股市的波动溢出效应十分显著,并且在次贷危机之后,美国股市对中国股市的风险传染性急剧上升。并使用Granger检验,检验数据稳健性。
郭全毓(2017) [7] 《沪、港、深股市的动态相关性研究——基于DCC-GARCH模型》使用DCC-GARCH模型分析深圳股市、上海股市及香港股市的动态相关系数,选取上海证券综合指数、深圳证券综合指数及恒生指数为指标,发现上海证券综合指数和深圳证券综合指数的关联性最高,深圳证券综合指数和恒生指数的动态相关系数与上海证券综合指数和恒生指数的动态相关系数相近,并对该现象做了解释。
莫悠、程锐(2017) [8] 在《基于向量自回归模型的中美股市联动性分析》中,选取了上海证券综合指数和标准普尔500指数作为指标,使用格兰杰因果检验后,使用VECM模型进行脉冲响应分析。
3. 综合指数协整检验
3.1. 数据选取
纳斯达克综合指数是可以反应纳斯达克证券市场行情变化的股票价格平均指数,基本指数为100。选取纳斯达克综合指数为代表变量,可以很好地反应在纳斯达克上市的各种新技术行业的公司的股价情况,涵盖软件、计算机、电信、生物技术、零售和批发贸易等。
上海证券综合指数简称上证综指,其样本股是在上海证券交易所全部上市股票,包括A股和B股。反映了上海证券交易所上市股票价格的变动情况。
由于上述两个综合指数对两个股市的代表性,选取11年间每日上证综指及纳斯达克综合指数为代表指标,进行相关的验证及计算,由于上海证券交易所及美国股市的开市时间及闭市时间不同,当有一方股市缺少当天数据时,同样删除另一方股市的当天的数据。
3.2. ADF检验
对纳斯达克综合指数用Eviews分别做第一种情形Intercept、第二种情形Trend and intercept及第三种情形None的ADF单位根检验,
结果如表1所示。
由结果可知,在三种情形时,在5%的显著性水平下,均不应拒绝存在单位根的原假设,查看三种情况下的AIC、SC、HQ的值,如表2所示。
选取三种情形下存在最小AIC、SC、HQ个数最多的情形,即无截距项、无时间趋势的单位根过程。
对上海证券综合指数进行ADF单位根检验,结果如表3所示。
由结果可知,在三种情形时,在5%的显著性水平下,均不应拒绝存在单位根的原假设,查看三种情况下的AIC、SC、HQ的值,如表4所示。
选取三种情形下存在最小AIC、SC、HQ个数最多的情形,即无截距项、无时间趋势的单位根过程。
3.3. 单整阶数
对纳斯达克综合指数进行一阶差分后,在进行三种情形下ADF单位根检验,结果如表5所示。

Table 1. Unit root test for Nasdaq Composite Index in three situations
表1. 对纳斯达克综合指数在三种情形下进行单位根检验

Table 2. Optimal criteria test for Nasdaq Composite Index
表2. 对纳斯达克综合指数最优准则检验

Table 3. Unit root test for Shanghai Composite Index in three situations
表3. 对上证综指在三种情形下进行单位根检验

Table 4. Optimal criteria test in three situations
表4. 三种情形下最优准则检验

Table 5. Unit root test for first-order difference of Nasdaq Composite Index
表5. 对纳斯达克综合指数的一阶差分的单位根检验
查看三种情况下的AIC、SC、HQ的值,如表6所示。
表明该序列是一阶差分平稳序列,即一阶单整。
对上海证券综合指数进行一阶差分后,在进行三种情形下的ADF单位根检验,结果如表7所示。
由结果可知,在三种情形时,在5%的显著性水平下,均应拒绝存在单位根的原假设,查看三种情况下的AIC、SC、HQ的值如表8所示。
表明该序列是一阶差分平稳序列,即一阶单整。
3.4. 协整检验
由上节可知,纳斯达克综合指数和上海证券综合指数均为一阶单整序列,可以使用Eviews进行协整检验,即先建立协整方程,后进行ADF单位根检验。结果如表9所示。
由上图表可知,存在单位根的概率为0.2812,在0.05的显著水平下,不应拒绝协整方程残根有单位根的原假设,可以判断两个综合指数间不存在协整关系。
4. 格兰杰因果检验
4.1. 数据选取
纳斯达克综合指数是可以反应纳斯达克证券市场行情变化的股票价格平均指数,基本指数为100。选取纳斯达克综合指数为代表变量,可以很好的反应在纳斯达克上市的各种新技术行业的公司的股价情况,涵盖软件、计算机、电信、生物技术、零售和批发贸易等。

Table 6. Optimal criterion test for the first-order difference of Nasdaq Composite Index
表6. 对纳斯达克综合指数一阶差分的最优准则检验

Table 7. Unit root test for the first-order single sequence of Shanghai Composite Index
表7. 对上海证券综合指数的一阶单整序列的单位根检验

Table 8. Optimal criterion test for the first-order difference of Shanghai Composite Index
表8. 对上海证券综合指数一阶差分的最优准则检验

Table 9. Unit root test for residuals of cointegration equations
表9. 对协整方程残差的单位根检验
上海证券综合指数简称上证综指,其样本股是在上海证券交易所全部上市股票,包括A股和B股。反映了上海证券交易所上市股票价格的变动情况。
由于上述两个综合指数对两个股市的代表性,选取11年间每日上证综指及纳斯达克综合指数为代表指标,进行相关的验证及计算,由于上海证券交易所及美国股市的开市时间及闭市时间不同,当有一方股市缺少当天数据时,同样删除另一方股市的当天的数据。
从收集到的数据可以通过每日的开盘价通过以下公式:

算出每日收益率。
4.2. 收益率平稳性检验
4.2.1
. 纳斯达克综合指数每日收益率平稳性检验
由时间序列相关知识可知,在进行格兰杰因果检验前要先对该时间序列进行平稳性检验,证明平稳性后,才能进一步进行格兰杰因果检验,使用Eviews进行单位根检验。
首先计算纳斯达克综合指数每日收益率后,使用ADF检验检验是否存在单位根。结果如表10所示。
由此可知可知,纳斯达克综合指数每日收益率符合平稳性。
4.2.2
. 上海证券综合指数每日收益率平稳性检验
计算上海证券综合指数每日收益率后,使用Eviews进行ADF单位根检验,结果如表11所示。
由结果可知,在三种情形时,在0.05的显著性水平下,均应拒绝存在单位根的原假设,查看三种情况下的AIC、SC、HQ的值如表12所示。
由此可知可知,上海证券综合指数每日收益率符合平稳性。
4.3. 格兰杰因果检验
由上文可证明,纳斯达克综合指数和上海证券综合指数的每日收益率均符合平稳性。使用Eviews对纳斯达克综合指数和上海证券综合指数的每日收益率做格兰杰因果检验。
二阶至五阶滞后的格兰杰因果检验结果如表13所示。
由表10到表13,可知纳斯达克综合指数每日收益率是导致上海证券综合指数每日提收益率的原因。
4.4. 格兰杰因果检验原因分析
众所周知,自从1944年,二战后世界建立起了布雷顿森林体系,即以美元为中心的世界货币体系。由此可先美国对世界的影响。显而易见,随着经济的发展,越来越多人进入股票市场进行投资,与此同时,许多公司也会选择在发展到一定规模积极上市,融资,获得更多的资金支持。而随着贸易全球化,资本全球化的进程,世界各金融市场间的关联性越来越强。
因此当美国股市出现大幅波动时,很容易影响到美元汇率及国际市场贸易,从而影响其他国家的股市股价。
而于中国股市而言,虽然由于贸易全球化,中国股市可能会对美国股市有一定程度的影响,但是美国股市可能受其他因素影响更加深远,中国股市的影响无法很直观的体现在股价上。
5. VAR建模
5.1. 建立VAR模型
上章节已经证明纳斯达克综合指数的每日收益率及上海证券综合指数的每日收益率满足平稳性检验的要求,因此可以对两个序列进行VAR建模。

Table 10. Unit root test for daily yield rate of Nasdaq Composite Index
表10. 对纳斯达克综合指数每日收益率的单位根检验

Table 11. Unit root test for daily yield rate of Shanghai Composite Index
表11. 对上海证券综合指数的每日收益率的单位根检验

Table 12. Optimal criterion test for daily yield rate of Shanghai Composite Index
表12. 对上证综指的每日收益率的最优准则检验

Table 13. Granger causality test between daily yield rate of Nasdaq Composite Index and Shanghai Composite Index
表13. 对纳斯达克综合指数及上证综指每日收益率间的格兰杰因果检验
通过Eviews对两组数据进行建模,得到0到10阶滞后的AIC、SC及HQ值,结果如表14所示。
根据滞后长度准则信息选取最优滞后阶数,从表15可知,8阶滞后是最优滞后阶数。
接下来建立VAR(8)模型,并回归。
设纳斯达克综合指数收益率当期值为Xt,滞后a阶为Xt−a,设上证综指收益率当期值为Yt,滞后a阶为Yt−a,可以得出VAR方程如下:
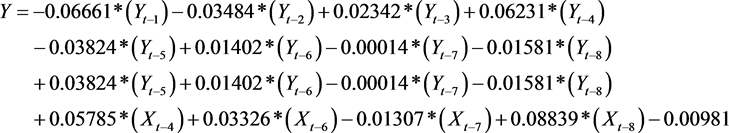


Table 14. Granger causality test between daily yield rate of Nasdaq Composite Index and Shanghai Composite Index
表14. 滞后0至10阶的VAR模型的最优准则检验

Table 15. VAR Model with lagging eight order
表15. 滞后8阶的VAR模型
Continued
5.2. 外生变量检验
对数据进行外生变量检验。
由表16可知,当被解释变量为上海证券综合指数每日收益率时,纳斯达克综合指数每日收益率不是内生变量的概率为0.0000,在0.05的显著水平下,应该拒绝纳斯达克综合指数每日收益率不是内生变量的原假设。因此,可以认为纳斯达克综合指数每日收益率是内生变量。
由表17可知,当被解释变量为上海证券综合指数每日收益率时,纳斯达克综合指数每日收益率不是内生变量的概率为0.0744,在0.1的显著水平下,应该拒绝纳斯达克综合指数每日收益率不是内生变量的原假设。而在0.05的显著水平下,不应该拒绝纳斯达克综合指数每日收益率不是内生变量的原假设。因此,可以判断纳斯达克综合指数每日收益率是内生变量。
5.3. VAR模型平稳性检验
由上节可知,在0.1的显著水平下,可认为纳斯达克综合指数收益率及上海证券综合指数收益率分别为彼此的内生变量,下一步应该对VAR模型进行平稳性检验,即单位根检验,如图1所示。
显而易见,该VAR模型具有平稳性。
5.4. 脉冲响应分析
证明了VAR模型的平稳性滞后可以进行脉冲响应分析,使用Eviews可以观察一次上证综合指数收益率的冲击,对上海证券综合指数每日收益率的滞后17期的情况,及纳斯达克综合指数每日收益率的一次冲击,对上海证券综合指数每日收益率的滞后17期的情况,情况如图2所示。
通过观察上述图2~图3,可以知道,两个指数对上海证券综合指数每日收益率的脉冲响应情况都较

Table 16. Exogenous variable test for daily yield rate of Nasdaq Composite Index
表16. 对纳斯达克综合指数每日收益率的外生变量检验

Table 17. Exogenous variable test for daily yield rate of Shanghai Composite Index
表17. 对上证综指每日收益率的外生变量检验

Figure 1. Unit root test for VAR Model
图1. 对VAR模型的单位根检验

Figure 2. Impulse response of Shanghai Composite Index to daily yield rate of Shanghai Composite Index
图2. 上证综指每日收益率对上证综指每日收益率的脉冲响应

Figure 3. Impulse response of Nasdaq Composite Index to daily yield rate of Shanghai Composite Index
图3. 纳斯达克综合指数日收益率对上证综指每日收益率的脉冲响应
为理想,在1到3期是冲击效果较为明显,而在10期之后的冲击效果逐渐趋于0。
同样通过观察图4~图5,可以知道,纳斯达克综合指数每日收益率对其本身的脉冲响应结果较好,但上海证券综合指数的每日收益对纳斯达克综合指数的每日收益率的脉冲响应结果不太理想,在第一期时,冲击效果接近于零,随后冲击效果急剧上升,最后趋于0,可以认为上海证券综合指数每日收益率对纳斯达克综合指数每日收益率有一定的影响,但影响不是即期的,有一定滞后。
5.5. 方差分解
进行脉冲响应分析之后,可以进一步进行方差分解。使用Eviews分解可以得出结果如下,表18是纳斯达克综合指数变动中归因于纳斯达克综合指数的比例。表19是纳斯达克综合指数变动中归因于上海证券综合指数的比例。
由表18可知,随着期数的增加,上证综指每日收益率能解释的纳斯达克综合指数每日收益率的贡献率逐渐增大,在九期滞后贡献率基本稳定在0.5%几乎无法解释纳斯达克综合指数每日收益率。
由表19可知,可以知道纳斯达克综合指数的每日收益率可以解释5%左右的上海证券综合指数的每
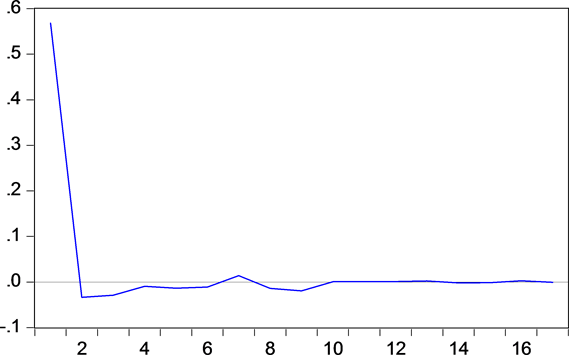
Figure 4. Impulse response of Nasdaq Composite Index's daily yield rate to Nasdaq Composite Index's daily yield rate
图4. 纳斯达克综合指数每日收益率对纳斯达克综合指数每日收益率的脉冲响应
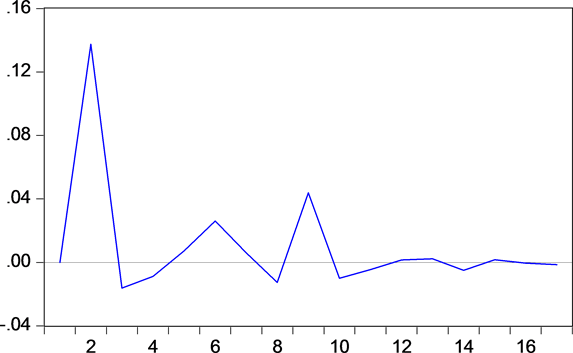
Figure 5. Impulse response of Shanghai Composite Index’s daily yield rate to Nasdaq Composite Index’s daily yield rate
图5. 上证综指每日收益率对纳斯达克综合指数每日收益率的脉冲响应
日收益率的波动。但上海证券综合指数及其之后阶数可以解释其近95%的波动。可以认为上证综指的每日收益率仍然主要由其本身解释。
6. 研究结论
通过单位根检验、单整阶数计算、格兰杰因果检验、VAR模型建模及脉冲响应分析等方法可以得出如下结论:
1) 纳斯达克综合指数及上海证券综合指数均为一阶单整序列。
2) 纳斯达克综合指数及上海证券综合指数不存在明显的协整关系,原因可能是因为缺少某些重要的影响因素。
3) 纳斯达克综合指数的每日收益率序列及上海证券综合指数的每日收益率序列均具有平稳性。
4) 在一定程度上,纳斯达克综合指数的每日收益率是造成上海证券综合指数的每日收益率波动的原

Table 18. Variance decomposition of Nasdaq Composite Index’s daily yield rate
表18. 纳斯达克综合指数每日收益率方差分解

Table 19. Variance decomposition of Shanghai Composite Index’s daily yield rate
表19. 上证综指每日收益率方差分解
因,而上海证券综合指数的每日收益率不是纳斯达克综合指数的每日收益率的原因。
5) 通过建立VAR模型,并通过相关检验发现最优的滞后阶数为八阶,而建立的VAR模型在一定显著水平下满足平稳性检验,而脉冲响应效益也较为良好。