1. 引言
近几年来,随着计算机领域的各个方面的快速发展,人类的生产生活中处处可见计算机的影子,尤其是3D打印技术的发展促使三维重建技术快速发展,这使得三维重建技术逐渐成为计算机领域的一个研究热点。不同领域的研究人员都致力于研究解决如何快速且便捷地获取三维信息。三维信息也被广泛应用于不同的领域,比如,机器人领域的自动导航以及计算机视觉中的自动识别物体,这两者都需要获取目标物体的精准的三维数据;建筑学中需要通过高精度的三维重建来实现预知建成效果;考古学中需要通过三维重建来实现对文物的保护以及维修工作。来自多个领域的大量需求要求三维重建需要有较高的精度。
依据使用的传感器的不同可以将三维重建的方法进行分类。第一类利用主动距离传感器,比如激光扫描仪 [1] [2] ,激光扫描仪通过激光扫描目标物体能够获得精准的三维信息从而构建出高精度的三维模型,但是该设备比较笨重而且价格昂贵,因而主要应用于科研领域。结构光法 [3] [4] 也能够构建高精度三维模型,但是需要借助投影仪的帮忙,而且在室外高亮度环境下难以工作,从而使得其只能局限于室内环境的应用。另一类方法用到被动距离传感器——摄像机。近年来,立体视觉 [5] [6] 被广泛地运用。不过该类方法一般需要固定相对位置且拍摄同步的两台摄像机来构成整个系统,同样使用较为复杂且价格不菲。相比之下研究仅利用一台手持式数码摄像机实现基于立体视觉技术的三维重建的方法,具有设备简易、使用方便以及成本低廉等长处,并且非常容易在其他领域得到推广应用。
2. 相关工作
自多视觉几何被提出以来,基于视觉的三维重建发展快速。Pollefeys [7] 等人的三维重建系统使用自带的单目摄像机绕着目标拍摄一系列的连续图像,通过处理这些图像来重建出三维模型,获取的图片越多重建出效果就越真实。但是该算法比较复杂,耗时较长。Snavely [8] 等人提出了一种基于无序互联网图像序列的视觉重建方法,但是其并不能获得一个致密的三维重建结果。A Geiger [9] 等人发明了一种基于双目立体视觉的实时三维重建方法,从而获得致密的三维重建结果,但是立体视觉系统结构比较复杂。中国科学院自动化研究所机器视觉课题组致力于视觉重建的发展和研究,他们利用多视角的高分辨率的建筑物图像就可以自动获取建筑物三维模型 [10] ,并将该技术应用在建筑保护方面。微软研究院(Microsoft Research)在2013年推出了Kinect Fusion项目 [11] ,Kinect Fusion利用Kinect传感器(深度相机)可以直接得到目标场景的深度图像数据,将传感器绕着目标物体或场景移动就可以获得不同角度下的多组深度图像数据并实时地构建场景三维模型。但是一开始传感器获取的数据会有很大的误差从而导致开头的重建模型很不精确。
本章针对现有三维重建算法的运算时间和精度两大研究热点提出了基于累积图和种子像素提取算法的高精度的三维重建系统。通过基于累积图快速NCC匹配算法来降低图像匹配的算法复杂度,从而大大降低了运算时间。利用种子像素提取算法获得的高置信度的种子像素,有效地减少了误配点,使得重建结果更加精准和真实。
3. 场景高精度三维模型重建算法
3.1. 算法概述
首先,获取同一个目标的两张图片。然后,计算两幅图对应的特征点,利用这些特征点计算获取两幅图像位置关系。接着,利用位置关系通过图像校正使得极线和扫描线的位置一致。最后,用一种基于种子像素点扩张技术的立体匹配算法:随机选择任意一个像素点,视为初始种子像素,运用初始种子像素通过计算可获得两幅视差图,再从两幅视差图中各自选取两个尺寸相同的窗口,通过比较两个窗口内相同位置的像素值就可以获得高置信度的种子像素,我们对这个高置信度的种子像素进行扩张,可以大大降低视差错误区域出现的可能性。同时提出一种基于累积图的快速NCC匹配代价计算方法从而高效地获得两幅图像对应的视差图,这样我们能得到快速准确的视差图。最后利用视差图和摄像机参数信息就可以得到目标场景的高精度三维模型重建结果。算法流程见图1。
3.2. 摄像机内参数标定
首先要获得单目摄像机的内参以及畸变系数,然后利用平面模板方法 [12] 计算相机内参数矩阵和镜头非线性畸变系数即通过摄像机标定过程计算未知的摄像机内部参数矩阵K和非线性畸变系数kc1、kc2。该方法利用了位于同一高度上的特征点通过计算可以获得摄像机内参的二个约束等式这个方法。通过拍摄不同位置的同一块标定板即可实现。
3.3. 图像采集和特征匹配
首先用摄像机对目标区域拍摄一幅图像;然后要求摄像机向与光轴指向基本垂直的方向运动一段距离,然后再次拍摄目标区域。两次拍摄只要求都能看到目标区域。
由于两幅图像之间视角相差较大,需要使用SIFT特征匹配算法 [13] ,对两幅图片进行特征匹配。然而一般的SIFT匹配比较粗糙,存在不少误配点,需要利用诸如RANSAC技术以减少错误点。特征匹配原图见图2。
3.4. 图像间相对位置计算
通过计算图像对对应的SIFT特征点得到一个齐次坐标集合,结合摄像机内参数K,通过8点算法以及RANSAC技术 [14] 可得到本质矩阵E。最终利用矩阵E可以获得旋转矩阵R和平移矢量T。
上述方法计算旋转和平移运动基于对代数误差的最小化,虽然速度较快但是缺乏几何意义。因此估计得到的运动参数精度不高,影响下一步的图像校正过程。所以需要对运动参数进行优化,这里可以采取非线性优化算法。本章使用的非线性优化算法基于极线约束关系,也就是说通过最小化SIFT特征点到其所在的极线的距离来获得优化的运动参数。
3.5. 图像校正
每幅图像都有极线和扫浙描线,为了使这两者对齐需要进行图像校正。当图像中的某一个像素点与对应图像中对应的像素点在同一扫描行上时,就使得图像匹配的问题得到简化,将匹配的复杂度从二维搜索降低到一维搜索。利用已知的相机内参和图像间的位置关系,我们设置两幅图使其相互平行,最后分别投影成新的平面图像。
图3显示了原图中的两幅图像进行图像校正并且进行了SIFT特征匹配的结果。从匹配结果可以看出,

Figure 2. The diagrams used in the experiment
图2. 实验原图

Figure 3. The result of SIFT feature matching of two corrected images
图3. 校正后的两幅图像SIFT特征匹配的结果
左右两幅图片匹配上的特征点在同一高度上,因此可以做立体匹配。
3.6. 立体匹配
为了获得两幅图中对应像素点之间的位移(通常称作视差),我们需要在两幅图像的每一个对应的像素点之间建立一种关系,通过立体匹配可以得到这种关系。然而,基于窗口的局部匹配运算速度较快但是产生误匹配区较多,而基于优化预设能量函数的全局优化匹配算法得出的视差图质量较高但是算法复杂。为了能解决算法功能和复杂度之间的矛盾,为此提出了一种同时具备上述两种算法优点的方法----基于种子像素扩张的图像匹配算法。
首先在立体图对中寻找一些匹配可信度较高的种子像素点,然后从这些种子像素点出发利用视差梯度约束来确定周围像素点的视差值。因为该算法利用置信度较高的种子像素点的视差值来约束周围像素点的视差搜索范围,从而降低了图中平滑区域误匹率;同时算法利用视差梯度约束保证了最终视差图的平滑性。该算法不运用能量函数并且不进行全局优化以此保证运算复杂度较低;该算法在扩张过程中兼顾了像素周围四邻域视差值产生的影响,因而不会像动态规划算法那样产生扫描行之间视差值不统一。
其次本章还提出了一种基于累积图的NCC匹配方法,该算法的计算复杂度和匹配窗口大小无关,因此加快了运算速度。
3.6.1. 基于累积图的快速NCC匹配代价计算
基于累积图的快速NCC匹配在经典的NCC匹配算法的基础上去除了大量的不必要的计算,简化了匹配搜索过程从而实现快速匹配,大大降低了计算复杂度。
NCC匹配代价为:
(1)
其中Wp为以像素
为中心的匹配窗口。
为I1中以
为中心的窗口中所有像素平均的亮度。
为I2中以
为中心的窗口中所有像素平均的亮度。若直接利用上述式子计算I1中每一个像素在每一个可能视差值处的匹配代价,则运算复杂度为O (WHDr |Wp|)。定义视差搜索范围为Dr且|Wp|为匹配窗口内像素的个数。通过分析可以知道,上式的计算复杂度受匹配窗口大小的影响。所以当立体图像对分辨率高时,需要比较大的匹配窗口,如果直接利用上式计算NCC匹配代价会很慢。
优化后的计算方式如下:
令Ik对应的累积图为iik,该累积图可以通过
快速计算。我们定义:
(2)
对于校正过后的立体图像对,计算方法有以下3步:
步骤1:根据立体图像对的分辨率设定匹配窗口Wp。
步骤2:计算累积图ii1和ii2。我们计算:
(3)
利用上新产生的两幅图像计算其分别对应的累积图ii11和ii22。
步骤3:设最小和最大视差搜索级分别为Dmin和Dmax。在仅考虑整数级别的视差级的情况下,可得:
(4)
对于视差搜索范围内的每一个视差搜索级d,其满足
,我们计算:
(5)
然后计算其对应的累积图ii12。最后计算视差搜索级为d时像素点p处的NCC匹配代价:
(6)
其中
是以坐标
的像素作为为中心像素的匹配窗口。
分析该算法复杂度:在步骤2中可知每一幅累积图的运算复杂度均为O (WH)。根据I11和I22的定义可知计算其中每一幅图像的运算复杂度也为O (WH)。为了得到它们对应的累积图需要额外的O (WH)运算复杂度。所以总运算复杂度为:
(7)
在步骤3中,当d固定时,计算I12的复杂度为O (WH)。利用I12,当d固定时,整幅图像的NCC匹配代价计算复杂度为O (WH)。因此对于某一固定的视差搜索级d,步骤3总的运算复杂度为
。由于需要遍历视差搜索范围中的每一个视差级,因此步骤3总的运算复杂度为O (WHDr)。本算法总的运算复杂度为步骤2和步骤3运算复杂度之和:
在前文中我们提到直接用定义式计算NCC匹配代价运算复杂度为O (WHDr |Wp|)。可见本算法的运算复杂度大大减小。
3.6.2. 种子像素提取算法
种子像素提取算法优化了种子像素的视差值,降低了其误匹配点,从而使得三维重建更加精确。该算法包括三个步骤:
步骤1:初始种子像素。因为初始种子像素不影响最终的种子像素。所以初始种子像素的数量以及视差值对最终结果的影响较小。当
满足下述下条件时认定为种子像素:
(8)
其中,
,由需要的种子像素点的多少和种子像素视差值的错误率决定。
步骤2:初始视差图生成。H为摄像机高度。
为初始种子像素,可得两个集合,分别为:
(9)
(10)
利用Su中的种子像素通过视差曲面扩张算法获得视差图Du,同理得出视差图Dd。通过这两幅视差图可以得出最后中种子像素。
步骤3:获取种子像素。定义视差图Du中位置
处的视差值为
,同理定义视差图Dd的视差值。选择各个边长均为2w + 1的矩形为窗口。如果公式(11),则
就是最终的种子像素:
(11)
当获取到所有的种子像素后,需要进行基于视差置信度的扩张。其扩张算法如下:
定义
处像素视差值为d,置信度为
,利用相似度衡量函数反映匹配点对的置信度,则取:
(12)
步骤1:创建像素的队列,对所有获取到的种子像素计算
并按照P的值从大到小填入队列中。
步骤2:上述队列不为空时,对队列开始的第一个种子像素做扩张计算。对于该种子像素的四邻域像素
,若该像素的视差值尚不存在,则视差值为:
(13)
若该像素的视差值已经存在且为d1,则新的视差值为:
(14)
如果队列为空则结束,输出视差图。
步骤3:若步骤2中没有生成新的种子像素时,删除队列开头的数据并再次做步骤2。否则计算每一个种子像素的
,并根据其值的大小按从大到小的顺序插入到队列相应位置,删除队列头部种子像素再重复步骤2。
4. 实验结果
本章使用的两组图像的分辨率为均716 × 591。数据集来自KITTI (http://www.cvlibs.net/datasets/kitti/eval_scene_flow.php?benchmark=stereo)。实验所用的电脑配置为:英特尔i5-6300核心处理器,8G内存,64位操作系统。
累积图的NCC匹配代价计算复杂度分析
我们比较本章提出的算法和直接利用NCC的定义式计算匹配代价。所有的实验均对两种算法使用相同的立体图像对,图4显示了实验结果。
在第一个实验中,视察搜索范围是90个视差级。我们使匹配窗口大小在4 × 4到24 × 24之间进行变化且我们仅分析计算NCC匹配代价消耗的时间。从图4(a)可以看到本章的算法不随匹配窗口大小的变化而变化,基本保持在3秒以内。然而直接使用定义式的NCC匹配算法法耗时随着匹配窗口尺寸的增大而迅速成二次曲线增长。图4(a)的结果符合我们在3.6.1中的分析。上述结果对于任意的矩形匹配窗口都是正确的。
在第2个实验中我们将匹配窗口的尺寸固定在17 × 17。让视差搜索范围在10到100个视差级之间变化,仅分析计算NCC匹配代价消耗的时间。从图4(b)可以看到两个算法的消耗时间都是随着视差级的增长而线性增加,但是本章算法的增长速度远慢于使用定义式的方法。
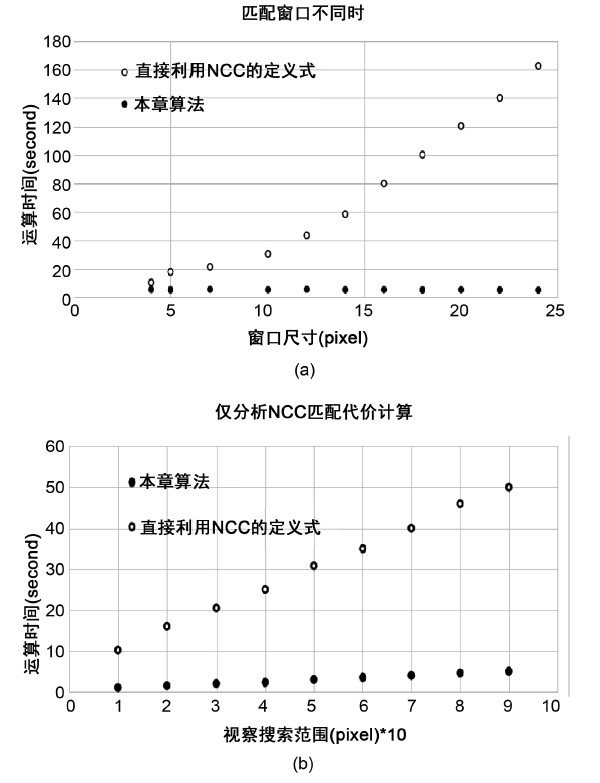
Figure 4. Comparison of computation time of NCC matching cost method. (a) Match the operation time different windows sizes. (b) Comparison of only NCC matching cost calculation is analyzed
图4. NCC匹配代价计算方法运算时间比较。(a) 当匹配窗口大小不同时的运算时间。(b) 仅分析NCC匹配代价计算时的运算时间
通过上述的2个实验,可以验证3.6.1中的理论分析:本章提出的NCC匹配代价计算方法运算复杂度为O (WHDr)。该运算复杂度远低于使用定义式的NCC匹配代价计算方法。
5. 重建结果
图5以及图6分别为两组室内场景的重建最终结果。
以上两组图片的第一行为原图,第二行第一幅为GRAPH CUT的左视差图结果,第二幅为本章算法立体匹配后的左视差图,第三行为重建结果。
从以上重建结果可以看出,利用GRAPH CUT得出的结果相对于本章提出的算法得出的结果来说图像的边缘部分以及细节部分像素值丢失严重(见图中红色方框标注处),并且图像本身噪声较多,这会导致最后的重建结果不够精准。而运用本章算法得出的视差图像素点饱满而且图像本身较平滑。所以本章提出的重建系统可以获得精度较高的三维场景。

Figure 5. Reconstruction results of NO. 1 indoor scene
图5. 室内场景重建结果1

Figure 6. Reconstruction results of NO. 2 indoor scene
图6. 室内场景重建结果2
6. 结论
本章我们提出了一种利用单台摄像机拍摄两幅图像从而获得场景高精度三维模型的算法。为简化算法的复杂度,本章使用差分求和定理对NCC相似度量函数进行了改进。利用种子像素提取算法自适应生成线状特征的直线模板,以此降低视差图的误配点。本章的方法对于获取两幅图像的方式要求不高,因此可以广泛用于多种场合。重建三维模型可以用于局部地形重建、考古学、无人机驾驶、机器人的自主导航等领域。所以,基于图像的三维重建既有理论意义也有广泛的应用价值。此外,本章提出一种基于种子像素扩张的立体匹配算法,降低了误匹配的概率。实验结果证明本章提出的方法能够适应多种不同的环境,产生真实的三维模型。
基金项目
浙江省公益技术应用研究计划项目(2016C33255);浙江省重点研发计划项目(2018C01086),2017年度浙江省大学生科技创新活动计划(2017R424018)。
参考文献
NOTES
*通讯作者。