1. 引言
近年来,EV数量持续上涨,其并网规模也日益增大。电动汽车充当分布式储能装置来参与电力系统调节,在电网中可在一定程度上发挥调频、调峰的作用,以应对电网的紧急情况。因此,电动汽车入网,一方面可响应国家政策,为社会带来显著的节能减排效益;同时,也对电网的可靠与经济运行带来促进作用。然而,电动汽车是电网的新型负载,在时空分布上具有较强的不可预测性,其充、放电行为也具有一定的间歇性与随机性。当电力系统大量接入电动汽车时,若其规模和接入模式控制不当,会对电网的负荷平衡、配网运行产生显著的负面效应 [1] ,为配网日常规划与正常运行增加新的难题。
电动汽车入网规划与运行控制,已经成为电力系统尤其是城市配电系统的研究热点。文献 [2] 预计今年美国PHEVs保有量将达到100万辆,且集中分布在重负荷区,若均在极端情况下同时充电对系统的影响是不可忽略的。文献 [3] [4] 以10 kV配电线路为接入点,结果显示当电动汽车渗透率逐步增加,网络中各母线节点的电压偏移也相应增加。文献 [5] 基于15 kV配电网,探究了电动汽车在不同分布及不同数量下充电情况。研究表明,当电动汽车充电时,存在网络损耗上升、线路传输实际功率越限等问题。文献 [6] 研究了多种充电模式及不同比例的EV接入配电网时的电压稳定裕度。文献 [7] 提出了一种大量电动汽车入网后的优化运行策略,并对电动汽车换电站入网的暂态稳定性进行研究。文献 [8] 采用IEEE-34节点系统,仿真分析不同分布及数量的电动汽车同时充电对配电系统网络损耗及电压的影响。文献 [9] [10] [11] [12] 发现只有增加当前发电量,才能与新增的电动汽车负荷量相匹配。文献 [13] 提供了评估EV数量及分布对配电网运行费用及能量损耗的综合性方法,并进行仿真分析,结果显示电动汽车占汽车总量为60%时,配网投资成本将增加15%,非高峰时段的能量损失将增大至40%。文献 [14] 基于PSCAD仿真系统,给出谐波抑制的方法。文献 [15] 搭建了一种EV充电负荷的时空预测模型,仿真得出EV渗透率较高时会在负荷高峰时段增加配电网负担,部分节点电压产生大面积越界的情况,对电网安全造成威胁。文献 [16] 基于需求侧响应,发现EV在有序充电时能够优化系统负荷特性,减少系统的峰谷差;文献 [17] 提出了一种以插电式EV作为储能设备的智能家居需求侧管理控制策略;文献 [18] [19] 为了减小EV并网导致的变压器负荷过载情况,给出相应的需求侧响应策略;文献 [20] 表明EV在参与电网互动时,换电站与电网公司双方均可获得更高的利润,此外也增加了分布式电源(DG)的利用率。
上述研究大都是基于单个网络节点电动汽车接入模式下的研究,并未考虑到多点同时接入时对电网影响的叠加效应。本文基于EV多点接入模式,探究多种接入模式下,EV接入电网后对电网负荷特性、电压偏移率的作用规律,并计算了电网的薄弱区域及线路裕度,基于PSASP仿真系统,对不同时空特征下的电动汽车接入配电网运行稳定性进行了分析计算。本文的研究成果,对于大规模EV的入网规划与运行控制具有积极意义。
2. 电动汽车入网模式分析
图1为EV群通过充电桩与系统互动的示意图。基于电动汽车入网供电(V2G)控制中心的角度,可将随机接入的电动汽车看作一个“整体”,将每一个充电桩等效为一个“智能充电桩”,即认为电动汽车通过一个虚拟的“等效智能充电桩”接入电力系统,与系统进行互动 [21] 。
3. 静态电压稳定分析原理
当今电网的发展趋势为大机组、多电网互联;而电网在长线路运行、负荷急剧增大以及无功储备不充足方面所带来的隐患逐步凸显,在故障状态及大负荷的共同影响下,负荷较大线路传输的功率极易超出其传输极限,进而电网潮流方程无解或不存在潮流平衡点,出现静态电压不稳定的现象,结果会损失大量负荷甚至系统崩溃。
3.1. 潮流方程式的特征结构分析
设功率潮流方程 [22] 为:
(1)
式中:
指常规潮流雅可比矩阵,
指功率不平衡向量,
指电压不平衡向量。倘使
,可得出电网中负荷无功功率和节点电压变化量的表达式:
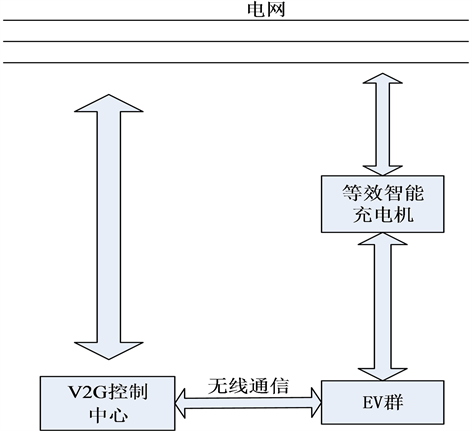
Figure 1. Schematic of electric vehicles accessing to power grid
图1. 电动汽车入网模式
(2)
电网的电压稳定可根据求出的
特征值加上特征向量来判别。以上则为模态分析法分析电压稳定性的基础方法。进一步对
进行特征值分解:
(3)
令
,则
(4)
其中:
,
为
的特征值;
为
的左特征向量;
为
的右特征向量。将式(4)代入式(2)可得:
(5)
其中:
为左特征向量阵
的第i行;
为右特征向量
的第i列。由式(5)得出:
(6)
令
,
,则有
(7)
式(7)中
,
分别为模态电压
和模态无功
变化量。由式(7),对第i个模式有:
(8)
式(8)中
为第i个模态无功对模态电压的相关度。当
极小甚至趋于零时,即模态无功的细微改变将致使模态电压产生剧烈改变,即电网可能失稳。综上,电压崩溃能够与模态电压崩溃相对应 [23] 。
3.2. 薄弱节点和薄弱区域的确定
根据式(5),母线k的V-Q灵敏度可表示为:
(9)
通过式(9)可得,V-Q灵敏度与单个母线电压的崩溃模式并无直接联系,而是参与V-Q改变的全部母线的叠加效果。为了与电网的薄弱节点、薄弱区域的判别相联系,引入“母线参与因子”:
(10)
这里
决定了
在母线k对V-Q灵敏度的影响。由于
可视为实对称矩阵,因此它的特征值为实数。基于此,电网中薄弱节点的判断核心即找出
的最小模特征值(主导特征值)以及与此最小模特征值相关的各节点参与因子的最大者 [23] 。
4. 算例仿真
4.1. 算例系统
本文仿真系统为New England某10机39节点网络,图2为其原始潮流。此网络含有10部同步发电机、12部变压器、34个线路以及39个系统节点,31号节点是平衡节点,出力不受限制。该网络分为两个区域,以母线39、3、18、16和21为界,图中虚线上部为区域一,其下部为区域二。系统基准功率为100 MVA,基准电压为345 kV。其网络线路参数见表1。

Figure 2. Network flow of New England system
图2. 网络潮流图

Table 1. Line parameters of New England system
表1. 线路参数表
4.2. 仿真分析
由文献 [24] 可知,大多数燃油车辆一天内只有5%左右的时间是行驶状态,剩下几乎95%的时间处于空闲状态。基于此,本文假设EV和普通燃油车停驶概率分布相同。图3表示一天内EV停驶概率
分布 [25] 。
本文基于图3所示的电动汽车停驶率,在New England的10机39节点网络中,选取编号为3、16、21三条母线上集中式的接入电动汽车,并分别计算这三条母线单独接入、两两母线组合接入以及三条母线同时接入电动汽车负荷时,电网的负荷波动、网络损耗以及电压偏移情况。仿真计算时,系统原有负荷维持原值,各发电机的输出能力不变。
4.2.1. 电动汽车接入对负荷的影响
图4为在停驶率基础上的电网负荷波动计算结果,其计算条件主要包括三条母线共同接入、两条母线同时接入、单条母线单独接入的接入模式。
图4中,曲线1表示电力系统内某省会城市夏季典型日负荷统计情况,其初始峰谷差20.26 MW。曲线2表示一条母线接入电动汽车后电网的日负荷曲线的变化,可以看到其峰谷差变为19.697 MW,其峰
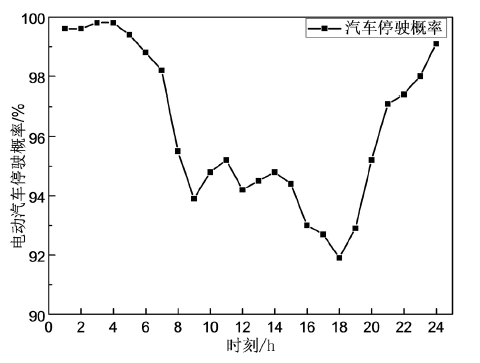
Figure 3. Probability of a vehicle to be parked
图3. 电动汽车停驶概率

Figure 4. The impact of electric vehicle access on power grid load
图4. 电动汽车接入对电网负荷的影响
值降低了0.67%,谷值相比增加了1.4%。曲线3表示两条母线同时有EV接入时电网的日负荷曲线的变化;可以看到其峰谷差变为19.134 MW,其峰值减小1.34%,谷值相比增加2.79%。曲线4表示三条母线同时接入电动汽车后电网的日负荷曲线的变化,可以看到其峰谷差变为18.571 MW,其峰值降低2.02%,谷值相比增加4.2%。可以看出,电动汽车的接入对原电网负荷有明显的平抑效果。
为了更好的表示其平抑程度,这里引入负荷波动率
。其定义为:负荷的标准差
与其几何平均数
的商。负荷的几何平均数
可以表示负荷的聚集水平,标准差 则可以表示负荷的离散水平,负荷的标准差
与几何平均数
的商就能够表示负荷离散的相对程度 [26]
则可以表示负荷的离散水平,负荷的标准差
与几何平均数
的商就能够表示负荷离散的相对程度 [26]
(11)
式中,
为标准差,
,
,表示一组日负荷曲线各时刻的负荷值,
指这组负荷数据的算数平均数。几何均值
。表2为负荷波动率的计算结果。
结合图4和表2,可以看到,随着接入母线数量的增大,负荷波动率也逐渐变小,表明负荷逐步集中,更加趋于稳定。上述现象表明,当电网中接入电动汽车时,具有削峰填谷效果,可有效平抑负荷波动。并且,当三条母线均有电动汽车接入时,其平抑效果更加明显。这是由于在上午8:00~11:00的负荷高峰时段,电动汽车通过入网放电主动承担了部分电力系统的负荷,而在负荷低谷时段2:00~8:00中EV的有序充电不仅能够节约用电成本,在未来的发展中,EV也可以充当备用电源。
4.2.2. 电动汽车入网对节点电压的影响
对于电力系统节点电压的波动程度可由电压偏移率来衡量,其定义式为:
(12)
上式中,U指电压实时数值,Uref为系统原始电压。
图5为三条母线共同接入、两条母线同时接入,单条母线接入等接入模式下,母线3的电压偏移率的计算结果。
图中曲线1表示仅母线3接入电动汽车,其最大电压偏移量为0.7893%;曲线2、3分别表示仅母线15、21单条母线接入模式,其最大电压偏移分别为0.2616%、0.1174%;曲线4表示母线3、16共同接入模式,其最大电压偏移量为1.0661%,比母线3和母线16单独接入模式的电压偏移率之和1.0509%大;曲线5表示母线3和母线21共同接入模式,其最大电压偏移量为0.9218%,比母线3和21单独接入模式下的电压偏移率之和0.9067%要大;曲线6表示母线16和母线21共同接入电动汽车,其最大电压偏移量为0.4009%,比母线16和母线21单独接入电动汽车的电压偏移和0.379%大;曲线7表示母线3、母线16和母线21共同接入电动汽车最大电压偏移量为1.2205%,比2条母线同时接入模式下的电压偏

Figure 5. Voltage excursion of different access conditions of electric vehicles
图5. 电动汽车不同接入情况的电压偏移
移再加上另一条母线单独接入模式电压偏移和1.1683%大。
由图5可知,所有接入模式下的电压偏移率均满足国家标准。其中,相比于其他两种接入模式,三条母线共同接入模式下的电压偏移率,大于三条母线单独接入模式下电压偏移率之和,也大于两条母线同时接入与一条单独接入模式下的电压偏移率之和;并且,两条母线同时接入模式下电压偏移率也会比单条母线接入模式的电压偏移率之和要高。这说明与单条母线接入模式相比,多点同时接入电动汽车时,其电压偏移会有叠加效果。在实际应用中,应注意电压偏移的叠加效应对电网正常运行带来的影响。尤其是在10:00~19:00时段,由于其电压偏移量相对较大,更应注意电动汽车在多点接入情况下的电网电压越限问题。
4.2.3. 电动汽车入网对母线参与因子的影响
PSASP以模态分析方法来寻找网络中的薄弱节点及区域,在初始运行点与电压稳定极限点处分别进行模态分析,进一步得出各节点对主导电压失稳的参与因子,由参与因子的大小来判断电网的薄弱节点区域。参与因子越大即此节点越薄弱。表3为初始/极限运行点处节点母线参与因子的计算结果 [23] 。
由表3可以看到,初始运行状态下,电网最薄弱的母线为母线12;电压稳定极限点时,母线6参与因子最大,因此为最薄弱节点,最薄弱的区域在母线5~8附近,如图2中矩形框所示。结合网络结构可以看出,薄弱区域中母线上所接负荷均相对较大,电压情况相对恶劣。随着电动汽车接入母线数量的增加,电网中各母线的参与因子发生了改变,电压初始点参与因子也会增加,而极限点参与因子有增加也有减少,这表明系统内薄弱母线也会随负荷的改变而变化。在初始/极限点两种情况下母线30~39的参与因子很小,即这些母线具有很强的抗干扰能力,不易产生失稳。结合电网模型,可以看到其母线上接入的负荷都相对较小,均有发电机支持,无功与电压情况良好。此外,在初始点时,系统薄弱的节点较分散;而在极限点处,薄弱节点分布更加集中。上述表明,在电压稳定极限点处,当薄弱节点电压不稳定时,其周围节点也会产生连环失稳,使电网产生重大的失稳事故。这也与实际电网中,相继的失稳故障常常在负荷较大的区域出现相符。
4.2.4. 电动汽车入网对线路裕度的影响
表4为部分线路裕度的计算。设线路原始功率
,极限点处功率P,定义线路的可传输裕度为
,则有:

Table 3. Results of bus participating factor for New England system
表3. 母线参与因子计算结果

Table 4. Calculation results of line margin (%)
表4. 线路裕度的计算结果(%)
(13)
基于PSASP软件,本文计算了部分线路在不同接入情况下的裕度值,如表4。图6为母线3在不同接入情况下的P-V曲线,图7为三条母线共同接入模式下不同母线的P-V曲线。
表4数据表明,随着接入母线数量的增加,各母线的线路裕度都在下降。这说明,随着负荷的增加,线路可承受的负荷容量在不断减少,且原始线路裕度相比其余线路大的母线,在电动汽车接入后其裕度并不一定大于其余线路裕度。即在负荷增长过程中,电压极可能是从裕度大的线路开始崩溃。
图6表明,对母线3来说,在不同的接入模式下,其线路传输功率也不尽相同。随着接入母线数量的增多,其电压稳定极限点左移,所对应的传输功率从4.21684、4.20759逐步下降到4.19865,在电压稳定极限点,其电压下降程度大致相似,均在0.92附近。
图7和表4中数据表明,相对于同一接入模式,虽然母线3、15、16的线路裕度存在差异,其中母线15与母线3较为接近,其功率传输极限点近似相同,但在电压稳定极限点处,母线3的电压最低可下降到0.92122,母线15的电压可下降至0.90551,而母线16则仅下降到0.96218。综上,即便线路裕度较大其线路母线的电压变化状况也应注意监控。
5. 结论
本文以负荷波动、电压偏移、模态分析、线路裕度等指标来评估EV接入对系统稳定的影响。结论表明,在有序充电时,EV的接入对系统的负荷曲线有显著的平抑效果。并且,不同接入模式下,系统的运行参数及稳定性也存在较大差异。
1) 多母线接入电动汽车时,其对电网削峰填谷作用最为显著,其峰值降低了2.02%,谷值增加4.2%。

Figure 6. P-V curve of busbar 3 under different access conditions
图6. 不同接入情况下母线3的P-V曲线
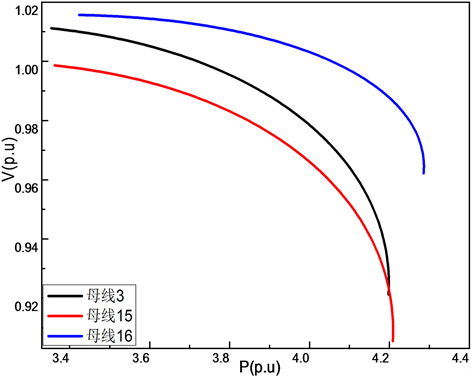
Figure 7. P-V curves of different buses at three-point access
图7. 三点接入时不同母线的P-V曲线
母线电压偏移率则可提升0.0522%。
2) 参与因子的大小与母线承受扰动的能力呈现负相关的趋势,即参与因子越小,母线承受扰动的能力越强;三母共同接入模式下,参与因子的波动最大,这说明多点同时接入电动汽车时,各母线可承受的扰动相比最小。
3) 随着接入母线数量的增加,线路裕度逐步下降。三母线接入时,线路裕度降低可降低3.33%。
此外,在系统负荷高峰时段,EV接入后虽可对其负荷曲线有一定的平抑作用,但此时段仍为一天中电网电压偏移较高时段,应控制入网电动汽车规模。