凸三角多面体的快速搜索

Fast Searching on Convex Deltahedra

摘要: 本文研究的图搜索模型是快速搜索，该模型与边搜索的区别仅是：搜索者不能“跳跃”且每条边只能被访问一次。本文研究的图是凸三角多面体，求解所有凸三角多面体的快速搜索数，提出关于凸三角多面体快速搜索数的相关推论。

Abstract: In this paper, we study fast searching graph searching model, which differs from the classical edge searching in one way: every edge is traversed exactly once and searchers are not allowed to jump. The graph of this paper is convex deltahedra. We will examine the fast search number (i.e., the minimum number of searchers required for capturing the fugitive) of all the convex deltahedra. We provide an explicit formula for the fast search number of convex deltahedra.

1. 引言

上世纪六七十年代Breisch [1] 与Parsons [2] 研究组建一支搜救队在洞穴里寻找丢失人员所需要的探勘人员的最少人数，称之为洞穴问题。Kirousis等在1986年提出了节点搜索 [3] 。Megiddo等在1988年提出了离散型的洞穴问题，称之为边搜索 [4] ，其核心问题是：在图上成功抓获入侵者最少需要多少个搜索者。节点搜索和边搜索是搜索博弈的两个基本模型。

本文研究的快速搜索是Dyer和Yang在2008年提出的一个改版的边搜索 [5] 。每条边只允许被搜索者访问一次且搜索者不允许有“跳跃”动作的单调的搜索博弈模型。数个搜索者在图上搜索一个自由且不可见的入侵者，即搜索者不知道入侵者的位置，入侵者却掌握搜索者的位置移动等信息。入侵者藏在要么顶点要么边上，并且可以在任一时间从当前顶点u沿着一条不含有搜索者的路径以非常快的速度移动到顶点v。当搜索者和入侵者占据同一个顶点时，入侵者被搜索者抓捕。搜索者的目的是成功抓捕入侵者，入侵者的目的是避免被抓捕并且总是选择最优策略进行逃脱。

在快速搜索中，搜索者可以有以下两种动作：

1) 放置：某一搜索者被放置到图上的一个顶点；

2) 移动：搜索者从当前顶点沿着一条未被清理过的邻边移动到邻点。

满足以下两个条件之一，搜索者就可以从顶点u沿邻边uv移动到邻点v：

1) 如果搜索者从顶点u移动到顶点v后，顶点u上还至少有一个搜索者；

2) 除边uv以外，顶点u的所有邻边都已被清理。

如果一条边uv可能藏有入侵者，则称该边是被污染的。如果可以确定一条边不藏有入侵者，则称该边是干净的。在某一时刻，如果图G的某一个顶点上至少有一个搜索者，则称该点被搜索者守卫。每条边通过搜索者的移动动作被清理。在博弈开始时，图上的每一条边都是被污染的，我们的目的是放置最少的搜索者来一步一步的清理该图的每一条边。

在快速搜索中，清理图G所需要的最少搜索者的数量称为图G的快速搜索数，记为 $fs\left(G\right)$ 。一个快速搜索策略是由满足最后一个动作结束整个图G被清理的一系列移动动作所组成的集合。以 $fs\left(G\right)$ 个搜索者清理图G的快速搜索策略被称为最优快速搜索策略。

单调性是搜索博弈的一个核心问题。一条边被搜索者清理后保持干净状态直至整个搜索策略结束，称这样的搜索策略具有单调性。以往的研究已证明边搜索、节点搜索和混合搜索具有单调性 [6] [7] ，连通边搜索不具有单调性 [8] 。

Dyer和Yang设计了一个线性时间复杂度的图搜索算法用来计算树的快速搜索数，并对二部图的快速搜索数做了相关研究 [5] 。2011年Stanley和Yang提出了一个快速搜索数的下界，并设计了计算立方体图和哈林图等的快速搜索数的图搜索算法 [9] 。2013年Yang等撰写了关于图搜索及其相关问题的综合性研究论文 [10] 。2016年Yang等得出了完全k部图的快速搜索数的一个上界与下界，并对完全二部图和完全分割图这两个特殊的完全k部图做了详细的研究 [11] 。2017年Xue和Yang提出了快速搜索的一个新下界，并提出了欧拉图和路径的笛卡尔积图的快速搜索数 [12] 。在两个基本模型的基础上，研究人员还提出了混合搜索、快速边搜索等搜索博弈的模型 [13] [14] [15] [16] [17] 。

图搜索在计算机科学、数学、物理领域引起了研究人员的浓厚兴趣。随着网络信息安全越来越得到重视，图搜索在网络安全、计算机游戏设计等领域得到了广泛的应用 [18] [19] 。经过多年的演进，在人工智能的很多分支领域都有所涉及图搜索 [20] [21] 。

本文研究在凸三角多面体上的快速搜索，目标求出凸三角多面体的快速搜索数。本文结构如下：第二部分给出相关的概念，第三部分求解凸三角多面体的快速搜索数并得出相关推论，第四部分进行全文总结。

2. 概念

本文分别用本文分别用 $V\left(G\right)$ 、 $E\left(G\right)$ 表示图 $G=\left(V,E\right)$ 的顶点集和边集，文中仅考虑简单连通图，即无环和无重边的图。

我们用uv表示连接顶点u和v的边，如果 $uv\in E\left(G\right)$ ，则称u和v是相邻的。对于图G中的任一顶点v的度是指v的邻边个数，记为 ${\mathrm{deg}}_G\left(v\right)$ 。如果一个顶点的度为奇数，称该顶点为奇点。类似的，当一个顶点的度数为偶数，称该顶点为偶点。当一个图的顶点都是奇点，称该图为奇图。对于任一点 $v\in V\left(G\right)$ ，集合 $\left\{u:uv\in E\left(G\right)\right\}$ 表示点v的所有邻点，记为 $N_G\left(v\right)$ 。 $\delta \left(G\right)=\min \left(\left|N_G\left(v\right)\right|:v\in V\left(G\right)\right)$ ，表示图G中最小的顶点度数。

三角多面体是指每一个面都是等边三角形的多面体。在凸三角多面体中，正四面体、正八面体和正二十面体是正则多面体。其余图属于约翰逊固体，一些顶点度数为3，一些顶点度数为4，一些顶点度数为5。值得注意的是，不存在18个面的凸三角多面体。

3. 凸三角多面体的快速搜索

首先求解所有凸三角多面体的快速搜索数，接着提出相关推论。

2011年Stanley和Yang [6] 提出如下推论和定理：

推论1：对于一个没有叶子节点的图 $G=\left(V,E\right)$ ，有 $fs\left(G\right)\ge \frac{1}{2}\left|V_{odd}\right|+2$ 。

定理1：对于一个连通立体图 $G=\left(V,E\right)$ ，设 $\tau$ 是图G的切点块图的叶子节块的数量，如果图G不包含切点，则 $\tau =2$ ，那么 $fs\left(G\right)=\frac{\left|V\right|}{2}+\tau$ 。

2011年Yang [13] 提出如下定理：

定理2：对于一个满足 $\delta \left(G\right)\ge 3$ 的连通图G，有 $fs\left(G\right)\ge \max \left\{\delta \left(G\right)+1,\lceil \frac{\delta \left(G\right)+\left|V_{odd}\left(G\right)\right|-1}{2}\rceil \right\}$

引理1：对于正四面体 $C_4$ ，有 $fs\left(C_4\right)=4$ 。

证：正四面体是一个连通立体图，显然不含有切点，又已知 $\left|V\left(C_4\right)\right|=4$ ，根据定理1得： $fs\left(C_4\right)=4$ (图1)。

引理2：对于双三角锥 $C_6$ ，有 $fs\left(C_6\right)=4$ 。

证：首先提出一个由4个搜索者组成的快速搜索策略：

Figure 1. Tetrahedron, triangular bipyramid

图1. 完全正四面体 $C_4$ 、双三角锥 $C_6$

1) 我们把搜索者 ${\lambda }_1$ 、 ${\lambda }_2$ 、 ${\lambda }_3$ 均放置到顶点 $v_1$ ，把 ${\lambda }_4$ 放置到顶点 $v_2$ ；

2) ${\lambda }_1$ 、 ${\lambda }_2$ 、 ${\lambda }_3$ 分别沿边 $v_1{v}_2$ 、 $v_1{v}_3$ 、 $v_1{v}_4$ 移动，使得 $v_2$ 、 $v_3$ 、 $v_4$ 分别被1个搜索者守卫；

3) ${\lambda }_4$ 从 $v_2$ 沿环 $v_2{v}_3{v}_4{v}_2$ 清理回到 $v_2$ ；

4) ${\lambda }_1$ 、 ${\lambda }_2$ 、 ${\lambda }_3$ 分别沿 $v_2{v}_5$ 、 $v_3{v}_5$ 、 $v_4{v}_5$ 移动到 $v_5$ ，完成对图 $C_6$ 的清理。即 $fs\left(C_6\right)\le 4$ 。

其次已知 $\delta \left(C_6\right)=3$ ， $\left|V_{odd}\left(C_6\right)\right|=2$ ，根据定理2得： $fs\left(C_6\right)=4$ (图1)。

引理3：对于正八面体 $C_8$ ，有 $fs\left(C_8\right)=5$ 。

证：首先提出一个由5个搜索者组成的快速搜索策略：

1) 我们把搜索者 ${\lambda }_1$ 、 ${\lambda }_2$ 、 ${\lambda }_3$ 、 ${\lambda }_4$ 均放置到顶点 $v_1$ ，把 ${\lambda }_5$ 放置到顶点 $v_2$ ；

2) ${\lambda }_1$ 、 ${\lambda }_2$ 、 ${\lambda }_3$ 、 ${\lambda }_4$ 分别沿边 $v_1{v}_2$ 、 $v_1{v}_3$ 、 $v_1{v}_4$ 、 $v_1{v}_5$ 移动，使得 $v_2$ 、 $v_3$ 、 $v_4$ 、 $v_5$ 分别被1个搜索者守卫；

3) ${\lambda }_4$ 从 $v_2$ 沿环 $v_2{v}_3{v}_4{v}_5{v}_2$ 清理回到 $v_2$ ；

4) ${\lambda }_1$ 、 ${\lambda }_2$ 、 ${\lambda }_3$ 、 ${\lambda }_4$ 分别沿 $v_2{v}_6$ 、 $v_3{v}_6$ 、 $v_4{v}_6$ 、 $v_5{v}_6$ 移动到 $v_6$ ，完成对图 $C_8$ 的清理。即 $fs\left(C_8\right)\le 5$ 。

其次已知 $\delta \left(C_8\right)=4$ ， $\left|V_{odd}\left(C_8\right)\right|=0$ ，根据定理2得： $fs\left(C_8\right)=5$ (图2)。

引理4：对于双五角锥 $C_{10}$ ，有 $fs\left(C_{10}\right)=5$ 。

证：首先提出一个由5个搜索者组成的快速搜索策略清理图 $C_{10}$ ：

1) 我们把搜索者 ${\lambda }_1$ 、 ${\lambda }_2$ 、 ${\lambda }_3$ 、 ${\lambda }_4$ 均放置到顶点 $v_2$ ，把 ${\lambda }_5$ 放置到顶点 $v_6$ ；

2) ${\lambda }_1$ 、 ${\lambda }_2$ 、 ${\lambda }_3$ 、 ${\lambda }_4$ 分别沿边 $v_2{v}_1$ 、 $v_2{v}_3$ 、 $v_2{v}_5$ 、 $v_2{v}_6$ 移动，使得 $v_1$ 、 $v_3$ 、 $v_5$ 、 $v_6$ 分别被至少1个搜索者守卫, ${\lambda }_5$ 从 $v_6$ 沿环 $v_6{v}_4{v}_3{v}_7{v}_6$ 清理回到 $v_6$ ；

3) ${\lambda }_1$ 、 ${\lambda }_3$ 分别沿 $v_1{v}_4$ 、 $v_5{v}_7$ 移动，使得 $v_4$ 、 $v_7$ 被一个搜索者守卫；

4) ${\lambda }_5$ 从 $v_6$ 沿环 $v_6{v}_4{v}_3{v}_7{v}_6$ 清理回到 $v_6$ ， $v_6$ 上的 ${\lambda }_3$ 清理 $v_7{v}_4$ ，完成对图 $C_8$ 的清理。即 $fs\left(C_{10}\right)\le 5$ 。

其次已知 $\delta \left(C_{10}\right)=4$ ， $\left|V_{odd}\left(C_{10}\right)\right|=2$ ，根据定理2得： $fs\left(C_{10}\right)=5$ (图2)。

引理5：对于变稜双五角椎 $C_{12}$ ，有 $fs\left(C_{12}\right)=5$ 。

证：首先提出一个由5个搜索者组成的快速搜索策略：

1) 把搜索者 ${\lambda }_1$ 、 ${\lambda }_2$ 、 ${\lambda }_3$ 、 ${\lambda }_4$ 均放置到顶点 $v_2$ ，把 ${\lambda }_5$ 放置到顶点 $v_4$ ；

2) ${\lambda }_1$ 、 ${\lambda }_2$ 、 ${\lambda }_3$ 、 ${\lambda }_4$ 分别沿边 $v_2{v}_1$ 、 $v_2{v}_3$ 、 $v_2{v}_4$ 、 $v_2{v}_5$ 移动，使得 $v_1$ 、 $v_3$ 、 $v_4$ 、 $v_5$ 分别至少被1个搜索者守卫, ${\lambda }_5$ 从 $v_4$ 沿环 $v_4{v}_5{v}_3{v}_1{v}_4$ 清理回到 $v_4$ ；

3) ${\lambda }_1$ 、 ${\lambda }_5$ 分别沿 $v_1{v}_6$ 、 $v_4{v}_6$ 移动(此时 $v_6$ 被2个搜索者守卫)；

4) ${\lambda }_4$ 沿 $v_4{v}_7$ 移动到顶点 $v_7$ ， $v_6$ 上的 ${\lambda }_5$ 沿路径 $v_6{v}_7{v}_5{v}_8$ 移动到 $v_8$ ；

5) ${\lambda }_4$ 沿 $v_7{v}_8$ 移动到 $v_8$ ，然后 $v_8$ 上的 ${\lambda }_5$ 沿 $v_8{v}_3$ 移动到 $v_3$ ；

6) $v_3$ 上的 ${\lambda }_5$ 清理 $v_3{v}_6$ ，完成对图 $C_{12}$ 的清理。即 $fs\left(C_{12}\right)\le 5$ 。

其次已知 $\delta \left(C_{12}\right)=4$ ， $\left|V_{odd}\left(C_{12}\right)\right|=4$ ，根据定理2得： $fs\left(C_{12}\right)=5$ (图3)。

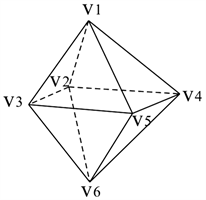
Figure 2. Octahedron, pentagonal bipyramid

图2. 完全正八面体 $C_8$ 、双五角锥 $C_{10}$

Figure 3. Snub disphenoid, triaugmented triangular prism

图3. 变稜双五角椎 $C_{12}$ 、三侧锥三角柱 $C_{14}$

引理6：对于三侧锥三角柱 $C_{14}$ ，有 $fs\left(C_{14}\right)=6$ 。

证：三侧锥三角柱的顶点布局为： $3\times 3^4$ 、 $6\times 3^5$ 。根据搜索者放置的初始顶点的度数，我们分为两种情况：

Case 1：初始顶点的度数为4，不失一般性，我们选取 $v_1$ 作为初始顶点。

1) 搜索者 ${\lambda }_1$ 、 ${\lambda }_2$ 、 ${\lambda }_3$ 、 ${\lambda }_4$ 均放置到顶点 $v_1$ ；

2) ${\lambda }_1$ 、 ${\lambda }_2$ 、 ${\lambda }_3$ 、 ${\lambda }_4$ 从 $v_1$ 沿领边进行清理，移动到其4个邻点 $v_2$ 、 $v_3$ 、 $v_4$ 、 $v_6$ (此时这4个搜索者不满足继续移动清理图的条件而只能守卫)；

3) 不失一般性，放置 ${\lambda }_5$ 到 $v_3$ ；

4) ${\lambda }_5$ 沿环 $v_3{v}_2{v}_6{v}_4{v}_3$ 清理回到 $v_3$ (此时 $v_3$ 有两条邻边未被清理且有2个搜索者 ${\lambda }_2$ 、 ${\lambda }_5$ )；

5) ${\lambda }_2$ 、 ${\lambda }_5$ 从 $v_3$ 分别沿邻边进行清理，移动到 $v_8$ 、 $v_5$ ；

此时5个搜索者所在的顶点上只有1个搜索者且其未被清理的邻边不止一条，所以这5个搜索者不满足继续移动清理图的条件。

Case 2：初始顶点的度数为5，不失一般性，我们选取 $v_2$ 作为初始顶点。

1) 放置 ${\lambda }_1$ 、 ${\lambda }_2$ 、 ${\lambda }_3$ 、 ${\lambda }_4$ 、 ${\lambda }_5$ 到 $v_2$ ，然后 ${\lambda }_1$ 、 ${\lambda }_2$ 、 ${\lambda }_3$ 、 ${\lambda }_4$ 、 ${\lambda }_5$ 分别沿邻边进行清理，移动到其5个邻点 ${\lambda }_1$ 、 ${\lambda }_3$ 、 ${\lambda }_4$ 、 ${\lambda }_5$ 、 ${\lambda }_7$ ，此时5个搜索者所在的顶点上只有1个搜索者且其未被清理的邻边不止一条，因此这5个搜索者不满足继续移动清理图的条件。

由上面分析可以得出：5个搜索者不足以成功地清理图 $C_{14}$ ，即 $fs\left(C_{14}\right)>5$ 。

其次需要证明 $fs\left(C_{14}\right)\le 6$ 。接着Case 1的第5步：

2) 我们再放置第6个搜索者 ${\lambda }_6$ 到 $v_6$ ，然后 ${\lambda }_6$ 从 $v_6$ 沿路径 $v_6{v}_8{v}_5{v}_2{v}_7$ 清理移动到 $v_7$ ；

3) ${\lambda }_4$ 从 $v_6$ 沿邻边 $v_6{v}_9$ 移动到 $v_9$ ，然后 ${\lambda }_2$ 从 $v_8$ 沿路径 $v_8{v}_9{v}_4{v}_7{v}_5{v}_9{v}_7$ 清理，完成对图 $C_{14}$ 的清理， 即 $fs\left(C_{14}\right)\le 6$ 。综上得证： $fs\left(C_{14}\right)=6$ (图3)。

引理7：对于双四角锥反角柱 $C_{16}$ ，有 $fs\left(C_{16}\right)=7$ 。

证：首先由于双四角锥反角柱的对称性，只要证明必要的几何元素具有某种性质，就足以概括其余，这是显然的。双四角锥反角柱的顶点布局为： $2\times 3^4$ 、 $8\times 3^5$ 。根据搜索者放置的初始顶点的度数，我们分为两种情况：

Case 1：初始顶点的度数为5，不失一般性，我们选取顶点 $v_3$ 作为初始顶点。

1) 放置 ${\lambda }_1$ 、 ${\lambda }_2$ 、 ${\lambda }_3$ 、 ${\lambda }_4$ 、 ${\lambda }_5$ 到 $v_3$ ；

2) ${\lambda }_1$ 、 ${\lambda }_2$ 、 ${\lambda }_3$ 、 ${\lambda }_4$ 、 ${\lambda }_5$ 从 $v_3$ 分别沿邻边进行清理，到其5个邻点 $v_1$ 、 $v_2$ 、 $v_6$ 、 $v_9$ 、 $v_4$ (此时这5个搜索者不满足继续移动清理图的条件而只能守卫)；

3) 放置 ${\lambda }_6$ 到顶点度数为4的顶点 $v_1$ 的邻点 $v_2$ 处(此时 $v_2$ 上有2个搜索者 ${\lambda }_2$ 、 ${\lambda }_6$ )；

4) ${\lambda }_6$ 沿环 $v_2{v}_6{v}_9{v}_4{v}_1{v}_2$ 清理回到 $v_2$ (此时 $v_1$ 有一条邻边未被清理且有1个搜索者 ${\lambda }_1$ )；

5) ${\lambda }_1$ 沿着邻边 $v_1{v}_5$ 到 $v_5$ ， ${\lambda }_2$ 沿邻边 $v_2{v}_5$ 到 $v_5$ (此时 $v_2$ 有一条邻边未被清理且有1个搜索者 ${\lambda }_6$ ， $v_5$ 上有2个搜索者 ${\lambda }_1$ 、 ${\lambda }_2$ )；

6) ${\lambda }_6$ 沿邻边 $v_2{v}_7$ 到 $v_7$ ；

由于 $v_5$ 上有2个搜索者，移动其中1个。此时根据 $v_5$ 的邻边未被清理的边的个数，可以分为以下两种情形：

(A) 选择有两条邻边未被清理的顶点

a) ${\lambda }_2$ 沿 $v_5{v}_4$ 移动到 $v_4$ (此时 $v_4$ 上有2个搜索者 ${\lambda }_2$ 、 ${\lambda }_5$ ，且只有一条邻边 $v_4{v}_8$ 未被清理)；

b) ${\lambda }_2$ 沿 $v_4{v}_8$ 移动到 $v_8$ ；

此时清理情况： ${\lambda }_1$ 、 ${\lambda }_2$ 、 ${\lambda }_3$ 、 ${\lambda }_4$ 及其所有邻边已经被清理；顶点 $v_5$ 、 $v_6$ 、 $v_9$ 有两条邻边未被清理(各点上1个搜索者)； $v_7$ 、 $v_8$ 、 $v_{10}$ 有两条邻边未被清理(各点上1个搜索者)，此时不满足继续移动清理图的条件；

(B) 选择有三条邻边未被清理的顶点

a) ${\lambda }_2$ 沿 $v_5{v}_7$ 移动到 $v_7$ ，此时 $v_7$ 上有2个搜索者 ${\lambda }_2$ 、 ${\lambda }_6$ ，可以移动其中1个；但是有三条邻边 $v_7{v}_6$ 、 $v_7{v}_8$ 、 $v_7{v}_{10}$ 未被清理，此时不满足继续移动清理图的条件；

b) 如果 ${\lambda }_6$ 沿边 $v_7{v}_8$ 移动到 $v_8$ ，由于此时 $v_8$ 上1个搜索者且四条邻边，此时不满足继续移动清理图的条件；

c) 如果 ${\lambda }_6$ 沿边 $v_7{v}_{10}$ 移动到 $v_{10}$ ，由于此时 $v_{10}$ 上1个搜索者且四条邻边，此时不满足继续移动清理图的条件；

i) 如果 ${\lambda }_6$ 沿 $v_7{v}_6$ 移动到 $v_6$ (此时 $v_6$ 有2个搜索者 ${\lambda }_3$ 、 ${\lambda }_6$ ，可以移动其中1个；且只有一条邻边 $v_6{v}_{10}$ 未被清理)；

ii) ${\lambda }_3$ 沿 $v_6{v}_{10}$ 移动到 $v_{10}$ ；

此时清理情况： $v_1$ 、 $v_2$ 、 $v_3$ 、 $v_6$ 及其所有邻边已经被清理( $v_6$ 上1个搜索者)； $v_4$ 、 $v_5$ 、 $v_7$ 、 $v_9$ 有两条邻边未被清理(各顶点上有1个搜索者)； $v_8$ 有五条邻边未被清理(0个搜索者)； $v_{10}$ 有三条邻边未被清理(1个搜索者)，此时不满足继续移动清理图的条件；

Case 2：初始顶点的度数为4，不失一般性，我们选取顶点 $v_1$ 作为初始顶点。

1) 放置 ${\lambda }_1$ 、 ${\lambda }_2$ 、 ${\lambda }_3$ 、 ${\lambda }_4$ 到 $v_1$ ；然后 ${\lambda }_1$ 、 ${\lambda }_2$ 、 ${\lambda }_3$ 、 ${\lambda }_4$ 从 $v_1$ 分别沿邻边进行清理，到其四个邻点 $v_2$ 、 $v_3$ 、 $v_4$ 、 $v_5$ ，此时这4个搜索者只能守卫而不能再移动；

2) 不失一般性，为了使清理继续下去，放置 ${\lambda }_5$ 到顶点 $v_2$ ；

3) ${\lambda }_5$ 沿环 $v_2{v}_3{v}_4{v}_5{v}_2$ 清理回到 $v_2$ (此时 $v_2$ 上上有2个搜索者 ${\lambda }_1$ 、 ${\lambda }_5$ 且有两条未被清理的边)；

4) $v_2$ 上的 ${\lambda }_1$ 、 ${\lambda }_5$ 沿邻边 $v_2{v}_7$ 、 $v_2{v}_6$ 到移动 $v_7$ 、 $v_6$ ；

此时清理情况： $v_1$ 、 $v_2$ 及其所有邻边已经被清理； $v_3$ 、 $v_4$ 、 $v_5$ 有两条邻边未被清理(各点上1个搜索者)； $v_6$ 、 $v_7$ 有三条邻边未被清理(各点上1个搜索者)； $v_8$ 、 $v_9$ 、 $v_{10}$ 及其所有邻边已经被清理；

显然此时这5个搜索者只能守卫而不能再移动；

5) 为了使清理继续下去，我们需要放置第6个搜索者 ${\lambda }_6$ 到图中，根据放置顶点处，未被清理边的个数，可以分为以下3种情形：

(A) 不失一般性，放置 ${\lambda }_6$ 到 $v_5$ (此时 $v_5$ 上有2个搜索者 ${\lambda }_4$ 、 ${\lambda }_6$ )；

a) ${\lambda }_4$ 、 ${\lambda }_6$ 移动到其邻点 $v_7$ 、 $v_8$ (此时 $v_7$ 上有2个搜索者 ${\lambda }_1$ 、 ${\lambda }_4$ )；

b) 移动 ${\lambda }_4$ 到 $v_{10}$ ，此时 $v_{10}$ 上只有1个搜索者，清理不能继续下去；

c) 移动 ${\lambda }_4$ 到 $v_8$ ，此时 $v_8$ 上有2个搜索者 ${\lambda }_4$ 、 ${\lambda }_6$ ，移动 ${\lambda }_6$ 到其一个邻点 $v_4$ ，再移动 ${\lambda }_6$ 到 $v_4$ 一个邻点 $v_9$ ，此时 $v_3$ 、 $v_6$ 、 $v_7$ 、 $v_8$ 、 $v_9$ 上有且只有1个搜索者且不止一条未被清理的邻边；显然此时这6个搜索者只能守卫而不能再移动，清理不能继续下去；

(B) 放置 ${\lambda }_6$ 到有四条邻边未被清理的顶点上；类上同证!

(C) 放置 ${\lambda }_6$ 到有五条邻边未被清理的顶点上；类上同证!

由上面分析可以得出：6个搜索者不足以成功清理图 $C_{16}$ ，即 $fs\left(C_{16}\right)>6$ 。

其次需要证明 $fs\left(C_{16}\right)\le 7$ 。接着Case 1(a)的第2步结束后，只需要在 $v_7$ 处放置1个搜索者 ${\lambda }_7$ ；然后 ${\lambda }_7$ 移动到 $v_8$ ； $v_7$ 上的 ${\lambda }_6$ 沿着路径 $v_7{v}_6{v}_{10}{v}_9{v}_8{v}_4{v}_3{v}_5{v}_8{v}_{10}$ 移动到 $v_{10}$ ，即完成对图 $C_{16}$ 的清理。

因此7个搜索者足以成功地清理图 $C_{16}$ ，即 $fs\left(C_{16}\right)=7$ (图4)。

引理8：对于正二十面体 $C_{20}$ ，有 $fs\left(C_{20}\right)=9$ 。

证明：首先需要证明 $fs\left(C_{20}\right)>8$ 。由于正二十面体的高度对称性，只需要证明一种情形，就足以概括其余，这是显然的。

1) 不失一般性，放置搜索者 ${\lambda }_1$ 、 ${\lambda }_2$ 、 ${\lambda }_3$ 、 ${\lambda }_4$ 、 ${\lambda }_5$ 到顶点 $v_1$ ，然后 ${\lambda }_1$ 、 ${\lambda }_2$ 、 ${\lambda }_3$ 、 ${\lambda }_4$ 、 ${\lambda }_5$ 分别沿着其邻边移动到 $v_2$ 、 $v_3$ 、 $v_4$ 、 $v_5$ 、 $v_6$ (此时显然不满足继续移动清理的条件)；

2) 分别放置 ${\lambda }_6$ 、 ${\lambda }_7$ 、 ${\lambda }_8$ 到 $v_2$ 、 $v_3$ 、 $v_4$ 上；

3) 移动 ${\lambda }_1$ 、 ${\lambda }_6$ 分别到 $v_7$ 、 $v_8$ ，移动 ${\lambda }_2$ 、 ${\lambda }_7$ 分别到 $v_8$ 、 $v_9$ ，移动 ${\lambda }_3$ 、 ${\lambda }_8$ 分别到 $v_9$ 、 $v_{10}$ (此时 $v_8$ 上有2个搜索者 ${\lambda }_6$ 、 ${\lambda }_2$ ，三条未被清理的邻边； $v_9$ 上有2个搜索者 ${\lambda }_7$ 、 ${\lambda }_8$ ，三条未被清理的邻边)；

4) ${\lambda }_6$ 、 ${\lambda }_7$ 分别沿 $v_8{v}_{12}$ 、 $v_9{v}_{12}$ 移动到 $v_{12}$ ，然后 ${\lambda }_6$ 分别沿 $v_{12}{v}_{11}$ 移动到 $v_{11}$ ；

此时未被清理的顶点上都有1个搜索者，并且这些顶点不止一条邻边未被清理，所以8个搜索者不足以成功地清理图 $C_{20}$ ，即 $fs\left(C_{20}\right)>8$ 。

其次未被清理的边构成欧拉子图且其每个顶点上都有1个搜索者，那么我们只需要放置1个搜索者到该欧拉子图的任一顶点上，该搜索者沿着欧拉回路就可以完成对图 $C_{20}$ 的清理。因此9个搜索者足以成功地清理图 $C_{20}$ ，即 $fs\left(C_{20}\right)\le 9$ 。综上得证： $fs\left(C_{20}\right)=9$ (图4)。

根据引理1~8我们得出如下推论：

推论1：对于凸三角多面体 $C_n$ ，有 $fs\left(C_n\right)=\max \left\{\delta \left(C_n\right)+1,\lfloor \frac{\delta \left(C_n\right)+\left|V_{odd}\left(C_n\right)\right|}{2}\rfloor +1\right\}$ 。

4. 总结

本文研究的是凸三角多面体的快速搜索问题。首先求解了凸三角多面体的快速搜索数，最后提出 $fs\left(C_n\right)=\max \left\{\delta \left(C_n\right)+1,\lfloor \frac{\delta \left(C_n\right)+\left|V_{odd}\left(C_n\right)\right|}{2}\rfloor +1\right\}$ 。在后续的研究中，我们也将对其他具有研究意义的

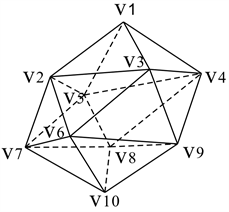
Figure 4. Gyroelongated square bipyramid, icosahedron

图4. 双四角锥反角柱 $C_{16}$ 、正二十面体 $C_{20}$

快速搜索问题展开研究。例如，树 $T_n$ 和路径 $P_n$ 的笛卡尔积图的快速搜索等都有待研究。