形状记忆合金管接头固紧力跌落数值仿真分析

Numerical Simulation Analysis on the Drop of Fastening Force of Shape Memory Alloy Pipe Connection

摘要: 形状记忆合金(Shape memory alloy, SMA)管接头固紧力跌落，会导致连接管件在后续使用过程中发生脱落，进而影响整个系统的安全可靠性。为系统研究SMA管接头的固紧力跌落规律，本文借助于非线性有限元软件ABAQUS二次开发用户自定义材料(UMAT)子程序，对不同管接头壁厚连接系统的装配过程进行数值模拟分析。研究结果表明：固紧力跌落发生在SMA管接头接触中间部位；相同管接头壁厚下，固紧力跌落现象在装配完成冷却前比冷却后更加明显；随着管接头壁厚增大，管接头内壁与被接管外壁之间接触压应力以及管接头内壁马氏体体积分数增大；管接头内壁的马氏体体积分数在管接头内壁中间部位发生不同程度的增大现象。本文工作可为SMA管接头的优化设计提供力学基础和技术参考。

Abstract: The drop of the fastening force of the shape memory alloy (SMA) pipe connection will lead to the fall off of the connecting fittings in the process of subsequent use, which will affect the safety and reliability of the whole system. In order to systematically study the drop law of the SMA pipe con-nection fastening force, the nonlinear finite element ABAQUS user-defined material subroutine (UMAT) program is employed to simulate the assembly process of the pipe connection system with different pipe connection wall thickness. The results show that the drop of the fastening force occurs in the middle part of the SMA pipe connection, and with the same wall thickness of SMA pipe connection, the drop of the fastening force is more obvious before cooling down during the assembly process. The contact pressure between the inner wall of the SMA pipe connection and the outer wall of the connected pipe, and the martensite volume fraction of the inner wall of the pipe connection gradually increase with the increase of the wall thickness of the SMA pipe connection; and in the middle part of the inner wall of the SMA pipe connection, the martensite volume fraction of the inner wall of the pipe connection increases to different degrees. The work in this paper can provide the mechanical foundation and technical reference for the optimization design of SMA pipe connection.

1. 引言

形状记忆合金(Shape memory alloy, SMA)自被发现以来，被广泛应用于航空航天、微机电系统、生物工程等领域 [1] [2] [3] 。不同于传统金属材料，SMA材料在热力耦合作用下，表现出独特的超弹性和形状记忆效应 [4] [5] 。其中，Ni-Ti形状记忆合金管接头就是利用SMA的形状记忆效应实现管路管线的固紧连接与密封 [6] ，并在军事科学领域内用于飞机、轮船等动力输油管路，相比于传统的连接方式，SMA管接头具有安装环境适应性好、可操作性高，安装过程简单等优点，且不会对系统内其它组件产生机械损伤。

近年来，为了提高SMA管接头的安全可靠性，降低实验成本，许多国内外学者对SMA管接系统进行了数值计算模拟。严金良等 [7] 采用Lagoudas三维本构模型和Total Lagrange增量法编制了SMA轴对称大变形有限元程序，利用轴对称模型对不同几何尺寸和扩径内压下的SMA管接头与被接管之间的接触压应力进行数值模拟。韩冬等 [8] 通过将管接头截面简化为不同圆环，模拟计算了TiNiFe-SMA管接头约束升温状态下紧固力的变化过程。郑雁军等 [9] 通过对Clausius-Clapeyron方程进行修正，建立在大预应变下的NiTi-SMA回复力模型。利用此模型，尹向前 [10] 和张慧博等 [11] 对TiNiNb管接头几何尺寸以及材料热胀系数对径向压应力的影响进行了数值分析。除此之外，智友海等 [12] 基于马氏体相变晶格理论，考虑马氏体不同变体种类，从细观力学角度推导了马氏体不同变体的相变驱动力方程，并采用有限元方法编制ABAQUS用户子程序，对有无垫/镀/涂层的SMA管接头和被接管交界面在不同的外载荷和边界条件下的脱粘部位进行了分析和研究。康泽天等 [13] 借助于有限元软件ABAQUS二次开发用户材料子程序，通过建立SMA管接头与被连接管的光滑无摩擦有限元模型，对SMA管接系统的装配过程进行数值模拟，讨论了管接头几何尺寸和扩径压力对管接头和被接管之间接触压应力水平和压力峰值的影响规律。

文献 [13] 发现管接头壁厚较大时，管接头内壁与被接管外壁之间产生的接触压应力在管接头内壁中间部位会发生跌落现象。为系统研究SMA管接头壁厚对固紧力跌落现象的影响规律，本文借助ABAQUS-UMAT程序，对不同SMA管接头壁厚下的管接系统的装配过程进行数值模拟并对不同管接头壁厚下的应力跌落现象进行对比分析，考察壁厚对SMA管接头相变行为以及管接系统在装配完成冷却前后管接头和被接管之间接触压应力跌落现象的影响，为SMA管接系统的设计和优化提供指导意义。

2. 理论模型

2.1. SMA本构关系

不考虑塑性应变，SMA的热力学应变表达式 [14] 为

${\epsilon }_{ij}={\epsilon }_{ij}\left(\xi ,T,{\sigma }_{ij}\right)={\epsilon }_{ij}^{\text{el}}+{\epsilon }_{ij}^{\text{tr}}+{\epsilon }_{ij}^{\text{th}}$ (1)

其中，马氏体体积分数 $\xi$ ，温度T和应力分量 ${\sigma }_{ij}$ 为内变量， ${\epsilon }_{ij}^{\text{el}}$ ， ${\epsilon }_{ij}^{\text{tr}}$ 和 ${\epsilon }_{ij}^{\text{th}}$ 分别表示弹性应变分量，相变应变分量和热应变分量。由式(1)，根据链式法则可得应变增量表达式为

$\text{d}{\epsilon }_{ij}=S_{ijkl}\text{d}{\sigma }_{kl}+{\Lambda }_{ij}\text{d}\xi +{\Theta }_{ij}\text{d}T$ (2)

式中， $\text{d}{\sigma }_{ij}$ ， $\text{d}\xi$ 和 $\text{d}T$ 分别表示应力张量增量分量，马氏体体积分数增量和温度增量， $S_{ijkl}$ ， ${\Lambda }_{ij}$ 和 ${\Theta }_{ij}$ 分别表示柔度张量分量，相变流动张量分量和热膨胀张量分量。

由复合材料力学夹杂理论，Brison [15] 将 $S_{ijkl}$ 和 ${\Theta }_{ij}$ 看作马氏体积分数的函数并表示为

$F\left(\xi \right)=\left(1-\xi \right)F_{\text{A}}+\xi F_{\text{M}}$ (3)

其中，F表示 $S_{ijkl}$ 和 ${\Theta }_{ij}$ ，下标“A”和“M”分别表示奥氏体和马氏体。

类比Mises塑性流动法则，SMA相变流动张量分量可以表示为

${\Lambda }_{ij}=\{\begin{array}{ll}\frac{3H}{2{\sigma }^{\text{eq}}}{\tilde{\sigma }}_{ij}\hfill & \stackrel{\dot{}}{\xi }>0\hfill \\ \frac{H}{{\bar{\epsilon }}^{\text{tr}}}{\epsilon }_{ij}^{\text{tr}}\hfill & \stackrel{\dot{}}{\xi }<0\hfill \end{array}$ (4)

式中，H为SMA在单轴拉伸过程中可产生的最大相变应变，

${\sigma }^{\text{eq}}=\sqrt{\frac{3}{2}{\tilde{\sigma }}_{ij}^2}$ (5)

表示等效应力， ${\tilde{\sigma }}_{ij}$ 表示偏应力张量分量，

${\bar{\epsilon }}^{\text{tr}}=\sqrt{\frac{2}{3}{\left({\epsilon }_{ij}^{\text{tr}}\right)}^2}$ (6)

表示等效相变应变。

由式(2)~(4)，可得SMA增量型本构关系为

$\text{d}{\sigma }_{kl}=C_{ijkl}\left(\xi \right)\left(\text{d}{\epsilon }_{ij}-{\Lambda }_{ij}\text{d}\xi -{\Theta }_{ij}\left(\xi \right)\text{d}T\right)$ (7)

式中， $C_{ijkl}\left(\xi \right)$ 为SMA材料的刚度张量分量，可对柔度张量进行逆运算求得。

2.2. SMA相变控制方程

采用Liang-Rogers余弦模型描述SMA在相变过程中马氏体体积分数与应力和温度之间的关系。假设SMA初始状态为奥氏体，当温度T满足 $T>M_{\text{s}}$ ，等效应力 ${\sigma }^{\text{eq}}$ 满足 ${\sigma }_{\text{ms}}\le {\sigma }^{\text{eq}}\le {\sigma }_{\text{mf}}$ 时，SMA发生正相变，此时马氏体体积分数为

$\xi =\frac{1}{2}\cos \left[\frac{\text{π}}{{\sigma }_{\text{ms}}-{\sigma }_{\text{mf}}}\left({\sigma }^{\text{eq}}-{\sigma }_{\text{mf}}\right)\right]+\frac{1}{2}$ (8)

式中， ${\sigma }_{\text{ms}}$ 和 ${\sigma }_{\text{mf}}$ 表示马氏体开始应力和结束应力，且在相变过程中，随着温度变化而发生变化，采用Brison线性方程对其变化关系进行描述

$\{\begin{array}{l}{\sigma }_{\text{ms}}={\sigma }_{\text{scr}}+C_{\text{M}}\left(T-M_{\text{s}}\right)\\ {\sigma }_{\text{mf}}={\sigma }_{\text{fcr}}+C_{\text{M}}\left(T-M_{\text{f}}\right)\end{array}$ (9)

其中， ${\sigma }_{\text{scr}}$ 和 ${\sigma }_{\text{fcr}}$ 表示马氏体开始应力和结束应力的初始值， $C_{\text{M}}$ 为马氏体应力影响系数， $M_{\text{s}}$ 和 $M_{\text{f}}$ 表示马氏体开始温度和结束温度。同样，采用Brison线性关系，奥氏体开始和结束应力可以表示为

$\{\begin{array}{l}{\sigma }_{\text{as}}=C_{\text{A}}\left(T-A_{\text{s}}\right)\\ {\sigma }_{\text{af}}=C_{\text{A}}\left(T-A_{\text{f}}\right)\end{array}$ (10)

当温度T满足 $T>A_{\text{s}}$ ，等效应力 ${\sigma }^{\text{eq}}$ 满足 ${\sigma }_{\text{af}}\le {\sigma }^{\text{eq}}\le {\sigma }_{\text{as}}$ 时，SMA发生逆相变，此时马氏体体积分数为

$\xi =\frac{{\xi }_0}{2}\left\{\cos \left[\frac{\text{π}}{A_{\text{f}}-A_{\text{s}}}\left(T-A_{\text{s}}-\frac{{\sigma }^{\text{eq}}}{C_{\text{A}}}\right)\right]+1\right\}$ (11)

式中， ${\xi }_0$ 表示逆相变开始时刻马氏体体积分数的初始值， $C_{\text{A}}$ 为奥氏体应力影响系数， $A_{\text{s}}$ 和 $A_{\text{f}}$ 表示奥氏体开始和结束温度。

2.3. 物理模型

图1所示为SMA管接系统的装配剖面示意图。SMA管接头内径3.00 mm，长度11.00 mm，初始壁厚t为1.40 mm，被接管外径为3.16 mm，壁厚0.58 mm。取被接管与管接头接触一端，长度13.00 mm。取管接头的对称结构并建立SMA管接系统的全尺寸有限元模型，考虑到实际工况，对管接头中间部位面上节点施加轴向位移约束，被接管远离管接头的端面上节点施加径向位移约束。在温度45℃时，对管接头进行扩径后卸载，将被接管插入到管接头中，对管接头加热至80℃与连接管接触进行固紧，然后将管接头冷却到加载温度45℃，完成整个装配冷却过程。

形状记忆合金管接头材料选取Ni-Ti合金，其材料参数如表1所示。E_A，E_M为奥氏体和马氏体的弹性模量，θ_A，θ_M为奥氏体和马氏体的热膨胀系数，假设奥氏体和马氏体泊松比相等同为μ，且在热力加载过程中保持不变。被接管选取某种双线性随动强化弹塑性合金材料，材料弹性模量为122 GPa，泊松比为0.325，屈服应力为992 MPa，强化模量为18,676 MPa。

3. 模拟结果及分析

通过对不同管接头壁厚下SMA管接系统的装配过程进行有限元数值模拟，得到装配完成冷却前后的应力分布情况。图2和图3所示为壁厚为2.50 mm，扩径内压为170 MPa时，装配完成冷却前80℃与冷却后45℃被接管与管接头对称结构的1/4模型的等效应力分布云图。可以看出，整个管接系统在装配完成冷却后的应力水平有明显降低，因此对装配完成冷却前管接头内壁与被接管外壁之间接触压应力的分析研究具有重要意义。

图4和图5所示为管接头壁厚为2.10 mm和2.50 mm时，SMA管接系统装配完成冷却前后管接头内壁与被接管外壁之间接触压应力沿管接头内壁的变化曲线。通过对比可知，随着管接头壁厚增大，冷却前和冷却后管接头内壁接触压应力水平均增大，且相较于临近区域，接触压应力均在管接头内壁中间部位均发生跌落现象。当管接头壁厚为2.10 mm时，该部位接触压应力在冷却前较临近区域下降约15.98 MPa，冷却后下降约18.02 MPa。当管接头壁厚为2.50 mm时，该部位接触压应力较临近区域冷却前下降约16.47 MPa，冷却后下降约19.49 MPa。通过对比以上数据，可以看出，相同壁厚情况下，管接头内壁中间部位的接触压应力在冷却后的跌落现象更加明显。

图6和图7所示为管接头壁厚为2.10 mm和2.50 mm时，SMA管接系统装配完成冷却前后管接头内壁马氏体体积分数沿管接头内壁的变化曲线。通过对比可知，随着管接头壁厚增大，管接头内壁与被接管外壁接触部位马氏体体积分数均增大。两种不同管接头壁厚的管接系统在冷却前后，管接头内壁马氏体体积分数均沿长度方向由两端向中间均先增大后逐渐减小后趋于稳定，但在管壁中间部位又突然增大。装配完成冷却前，不同壁厚管接头内壁与被接管外壁接触部位马氏体体积分数最大位置均出现在距离端口约0.2 mm处，当壁厚为2.10 mm时，马氏体体积分数最大约为0.78，当壁厚为2.50 mm时，马氏体体积分数最大约为0.82。装配完成冷却后，不同壁厚管接头内壁与被接管外壁接触部位马氏体体积分数最大位置出现位置不同，且当壁厚为2.10 mm时，马氏体体积分数最大位置出现在距离端口约0.2 mm处，

Figure 1. SMA pipe connection system assembly profile

图1. SMA管接系统装配剖面示意图

Table 1. Material parameters of NiTi shape memory alloy

表1. NiTi形状记忆合金材料参数 [13]

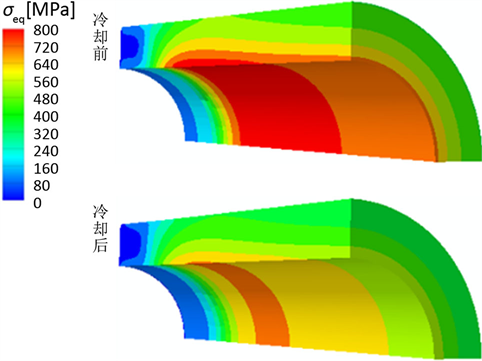
Figure 2. Equivalent stress distribution of the connected pipe before and after cooling down

图2. 冷却前后被接管等效应力分布云图

最大值约为0.86，当壁厚为2.50 mm时，马氏体体积分数最大位置出现在距离端口约0.1 mm处，最大值约为0.92。

4. 结论

通过有限元数值模拟不同管接头壁厚的形状记忆合金(SMA)管接系统的装配过程，并对装配完成冷却前后管接头内壁与被接管外壁之间接触压应力以及管接头内壁马氏体体积分数分布情况进行分析讨论，

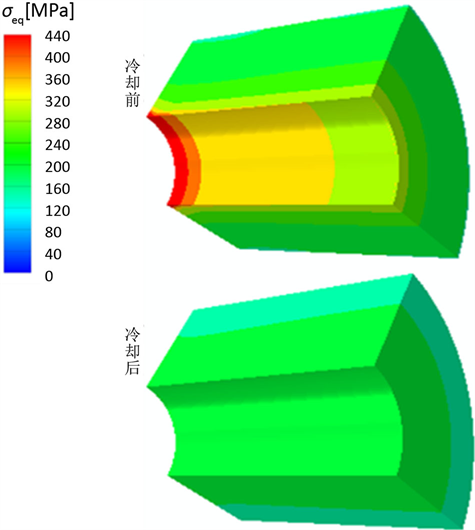
Figure 3. Equivalent stress distribution of the pipe connection before and after cooling down

图3. 冷却前后管接头等效应力分布云图

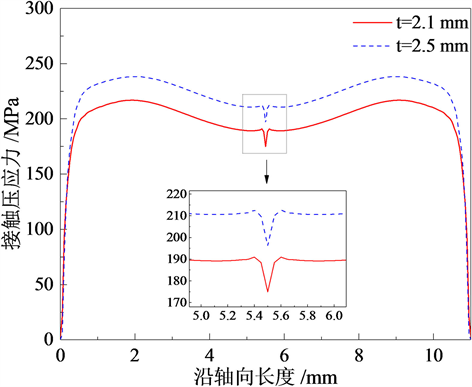
Figure 4. Contact pressure distribution curve of inner wall of pipe connection before cooling down

图4. 冷却前管接头内壁接触压应力分布曲线

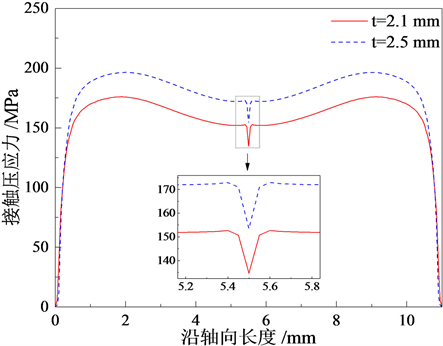
Figure 5. Contact pressure distribution curve of inner wall of pipe connection after cooling

图5. 冷却后管接头内壁接触压应力分布曲线

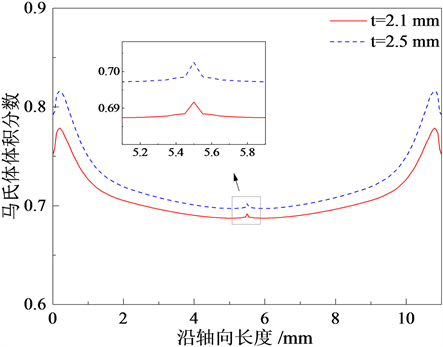
Figure 6. Martensite volume fraction distribution curve of inner wall of pipe connection before cooling down

图6. 冷却前管接头内壁马氏体体积分数变化曲线

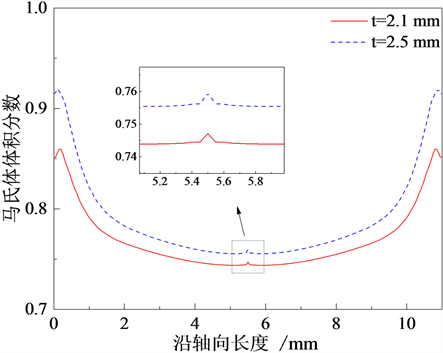
Figure 7. Martensite volume fraction distribution curve of inner wall of pipe connection after cooling down

图7. 冷却后管接头内壁马氏体体积分数变化曲线

得到以下结论：

1) 管接头内壁与被接管外壁之间接触压应力在接触中间部位发生跌落；

2) 随着SMA管接头壁厚增大，管接头内壁与被接管接触中间部位的接触压应力以及管接头内壁马氏体体积分数均增大；

3) SMA管接头壁厚较大时，管接头内壁与被接管接触中间部位的接触压应力在整个管接系统装配完成冷却前后均发生不同程度的跌落现象，且在相同壁厚下，冷却后的跌落现象相较于冷却前更加明显；

4) SMA管接头壁厚较大时，管接头内壁与被接管接触中间部位受力情况较为复杂，该部位马氏体体积分数较邻近区域在整个管接系统装配冷却前后均发生不同程度的突然增大。

基金项目

国家重点研发计划(2017YFC0307604)资助项目。