1. 引言
液晶(liquid crystals, LCs)中的拓扑缺陷是一种常见的位错。在单轴向列相液晶系统中,缺陷可根据其构型分为强度为
的点缺陷和强度为
的线缺陷 [1]。对于位于有界体积内的一个有序系统,处于平衡态的液晶系统包含一定数量的缺陷 [2],但缺陷强度总和为0。例如,对于球形微滴的超流体3He-A,平衡态时系统表面存在一些点缺陷,即boojum缺陷 [2][3]。同样,在一个具有垂直边界条件的向列相液晶微滴中,当系统到达平衡态时,会出现另一种体缺陷(hedgehogs) [4][5]。然而,当微滴的边界为沿面锚定时,液晶微滴中会产生双极结构:其特征是两个点缺陷(boojums)在微滴的两极 [2]。
Karlj和Rosso等人 [6][7]运用Landau-de Gennes 理论 [8],研究了一个包含+1缺陷的轴对称圆柱形液晶系统,上下基板分别为足够强的沿面锚定和足够强的垂直锚定,这样的几何限制和边界条件会在上基板诱导出一个boojum缺陷。当限制条件为几十纳米时,称这样的缺陷结构为手指形boojum (fingered boojum)。随后,Xiaoyu Jiang等人 [9]同样运用Landau-de Gennes理论和二维有限差分迭代法 [10]研究了一个包含−1缺陷的圆柱形简并混合排列向列相(DHAN)液晶盒,上下基板分别为强的垂直锚定和强的沿面锚定。当盒厚较大时会在下基板中心诱导一个boojum缺陷,对于该−1 boojum缺陷,其指向矢分布不具有轴对称性,但其双轴性分布具有轴对称性。当液晶的厚度减小到足够小(~20 nm)时,这两种液晶系统内均会诱导出有序重构(order reconstruction, OR)现象,即本征值交换。有序重构(本征值交换)现象首次由Schopohl和Sluckin在
楔形向错中发现 [11]。本征值交换即两个具有正交指向矢的单轴态在两个基板间互相交换,中间不存在本征矢的转动,但本征值随位置连续变化,且存在一系列双轴态连接两个单轴态。随后,向列相液晶薄盒中的缺陷结构 [12][13][14][15]成为研究热点。其中,陈思博等人在研究包含拓扑缺陷的混合向列相液晶薄盒时发现,当液晶系统的厚度减小到约27.4 nm时,系统由缺陷态转变为有序重构态,即发生本征值交换,我们定义此时的盒厚为临界盒厚 [15]。
由于液晶具有各向异性的力学和光学性质,因此,液晶中的球形胶体则具有强的各向异性相互作用 [16],并且这些系统的一个显著特征是具有拓扑缺陷 [17]。当具有强的切面锚定的球形胶体分散在液晶中时,一对拓扑表面boojum缺陷会出现在胶体粒子相反的两极 [18][19][20]。例如:Tasinkevychp [16]等人研究了一个以强切向锚定为特征的球形胶体粒子,通过改变锚定强度、胶体粒子半径和温度,讨论了三种类型的boojum缺陷核心(单核心、双核心和分裂核心)之间的结构转变。综上,圆柱形液晶系统与液晶中球形胶体上的boojum缺陷分别存在一定的研究,但没有将二者联系起来。本文在含有+1 boojum缺陷的圆柱形液晶系统的基础上,将上基板由平面基板换成半球状的曲面基板,建立一个含有+1 boojum缺陷的圆柱内切球液晶系统,研究该系统中boojum缺陷的结构特点。
本文运用Landau-de Gennes理论和二维有限差分迭代法 [10],研究了一个具有轴对称性的纳米级圆柱内切球向列相液晶系统,通过改变半径的大小和球形界面的边界条件,来观察+1 boojum缺陷的结构转变情况;并通过与相同条件下的圆柱形向列相液晶盒中的boojum缺陷结构进行比较,来研究球形界面对+1 boojum缺陷结构转变的影响。
2. 几何模型
在一个轴对称的圆柱形向列相液晶盒的基础上,将其上基板由平面基板设置为半球状的曲面基板,下基板保持不变。如图1(a)所示,将圆柱和球的半径设为R,圆柱的高度设为d,上下基板中心的距离设为h
,我们把该模型称为圆柱内切球液晶盒。由于该圆柱内切球液晶盒是轴对称的,所以本文只选取ρ-z平面的一半来说明液晶分子的排列情况。如图1(b)所示,液晶分子在上基板沿球面排列,在下基板垂面排列,对于对称轴和外壁我们采用自由边界条件。当上下基板均设置为足够强的锚定强度时,会在球形界面中心处诱导出一个+1 boojum缺陷。将图1(c)所示圆柱形液晶盒模型作为对比模型,其上基板液晶分子沿面排列,在下基板垂面排列。为了更好地比较(b)、(c)两种模型中+1 boojum缺陷结构的转变过程,图1(b)中选取abcd截面,图1(c)中选取
截面来进行研究。
采用柱坐标系
来建立模型,其对应的活动基为
,其中
沿半径方向,
沿对称轴方向,且有
。在柱坐标系下,指向矢可以写成
,
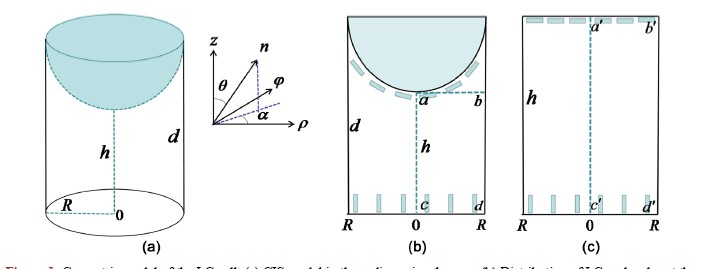
Figure 1. Geometric model of the LC cell. (a) CIS model in three-dimensional space; (b) Distribution of LC molecules at the spherical interface and lower substrates in ρ-z plane within CIS model; (c) Distribution of LC molecules at the upper and lower substrates in ρ-z plane within cylinder model
图1. 液晶盒的几何模型。(a)三维空间中的圆柱内切球模型;(b)在圆柱内切球液晶盒ρ-z平面内,液晶分子在球形界面和下基板处的分布情况;(c)在圆柱形液晶盒ρ-z平面内,液晶分子在上下基板处的分布情况
其中极角
为指向矢与z轴的夹角,方位角
为指向矢在ρ-φ平面的投影与
轴的夹角。
3. 理论方法
根据Landau-de Gennes理论,用序参数张量Q来描述液晶分子在三维空间下的有序程度,Q在主轴系中的表达式为 [21]
(1)
其中,
和
分别为Q的第i个本征值和本征矢。序参数张量Q是对称无迹的,满足
,
。当系统处于单轴态时,Q的三个本征值中有两个是相等的,序参数张量Q可以表示为
(2)
其中S为标量序参数,
为液晶分子的指向矢,I表示单位张量。当序参数张量Q的三个本征值都不相等时,系统处于双轴态。双轴性的大小用双轴性参数
来确定,
的表达式为 [22]
(3)
其取值范围为
。当
时,系统处于单轴态;当
时,系统具有最大的双轴性。
3.1. 自由能密度
液晶系统无外加电场作用时,Landau-de Gennes理论的总自由能密度表示为 [6]
(4)
其中
为只依赖于序参数张量Q的本体自由能密度,其具体的表达式为
(5)
其中A随温度T变化,表达式为:
,
为最低过冷温度,
,B和C为材料常数。设
为相变温度,当
时,
,系统处于各向同性相;当
时,
,系统处于各向异性相。弹性自由能密度
是由于液晶取向序的不均匀引起的,并且还依赖序参数张量Q的空间变化率。若只考虑Q及导数的二次项,则它的表达式为 [23][24]
(6)
其中,系数
与展曲(
),扭曲(
)和弯曲(
)弹性常数有关。为了简便,本文采用单一常数近似,将Frank理论中的三个弹性常数近似为K,即
,则得到
,则弹性自由能密度的表达式可以简化为
(7)
3.2. 边界条件
固定表面对液晶的锚定作用可通过序参数张量Q和锚定强度系数
来描述。界面对液晶指向矢分布的影响是通过表面自由能反映的,而锚定能代表的是表面自由能中的各向异性部分,同时也反映了基板对液晶分子锚定作用的强弱。
表示表面自由能密度 [25],其表达式为
(8)
其中,
为锚定强度系数,而W是通过Frank弹性理论得到的,
为基板上易取向方向的序参数张量 [26]。
弱锚泊边界条件为:
(9)
其中,
为垂直于基板的外法线方向的单位矢量。
3.3. 无量纲化
根据Karlj等人 [6]提出的约化方法对系统进行无量纲化处理,引入以下无量纲化参数:
,
,
,
,
和
,其中
是最高过热温度下的序参数,
是向列相相干长度,用来约化长度变量。则约化后的本体自由能密度为:
(10)
其中,
是约化温度。约化后的弹性自由能密度为:
(11)
约化后的表面锚定能密度为:
(12)
则约化后的弱锚定边界条件为
(13)
3.4. 动力学求解
基于之前的研究 [10][27],可得序参数张量Q的动力学方程为:
(14)
其中系数
,
是向列相液晶的转动扩散系数。对动力学方程进行约化
(15)
其中
。使用有限差分迭代法 [10],将上式离散成差分形式
(16)
其中,
(17)
4. 数值结果
模拟时采用液晶材料为5CB [28][29],各个参数的数值为:
,
,
,
。因此可得到相干长度
约为2.64 nm。约化温度设为
,相应的约化标量序参数取值为
,转动扩散系数
设为
[27]。在数值计算中,我们设圆柱的高度
不变,半径r的初值为
,则上下基板中心的距离为
,随着半径r的增大,h逐渐减小。
4.1. 强锚定边界条件
在球形界面和下基板均为强锚定的圆柱内切球液晶盒中,液晶分子在下基板垂面排列,在上基板沿面排列。当系统到达平衡态时,会在球形界面的中心处诱导出一个+1 boojum缺陷。首先逐渐增大液晶盒的半径,观察boojum缺陷的结构转变过程。随后,通过与相同边界条件的圆柱形液晶盒中的结构转变过程进行比较,研究球形界面对+1 boojum缺陷结构转变的影响。最后,通过对比序参数张量Q在对称轴
处的本征值图,来观察boojum缺陷结构中指尖位置的变化情况。
图2为在圆柱内切球液晶盒中,不同半径下的球形界面上的+1 boojum缺陷的双轴性局部放大图。图2(a)所示,当
时,在球形界面上诱导出了一个很小的+1 boojum缺陷结构,其他区域均为单轴态。继续增大半径,球形界面上的+1 boojum缺陷结构逐渐变大。当半径增大到
(图2(b))时,系统的双轴性结构开始发生变化,除了+1 boojum缺陷外还出现了一个缺陷环。继续增大半径,如图2(c)和图2(d)所示,缺陷环的双轴性逐渐变大,最后缺陷环沿着球形界面向上扩散。
为了更好的探究球形界面对boojum缺陷结构转变的影响,下面研究以R为半径,h为盒厚的圆柱形向列相液晶盒中boojum缺陷结构的转变过程。为了方便进行对比分析,把圆柱模型上下基板的锚定条件
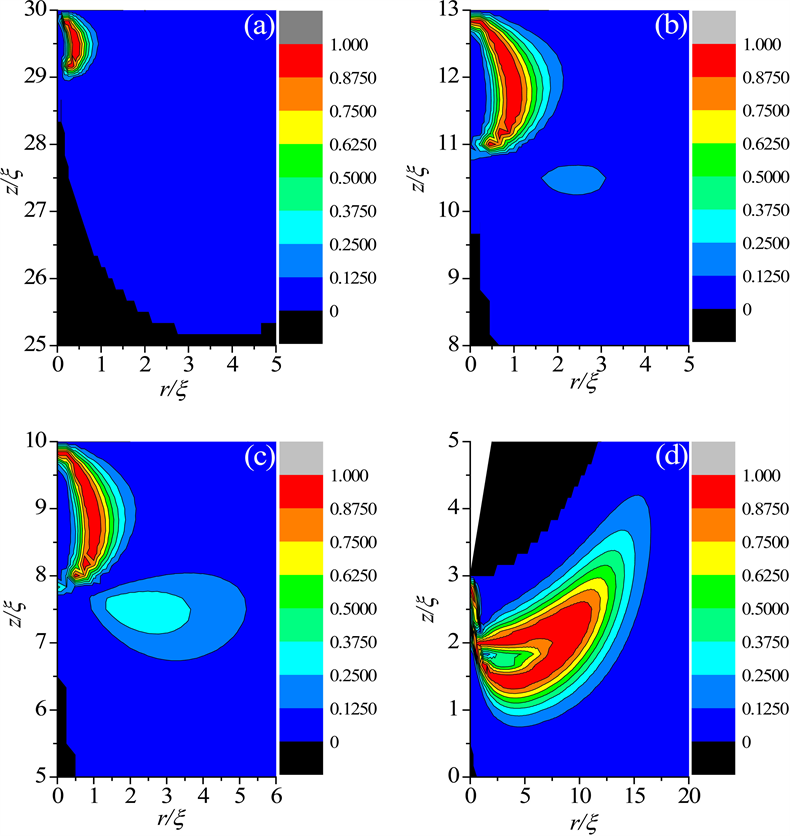
Figure 2. Biaxiality profiles of partial enlargement of +1 boojum defect in CIS LC cell. (a)
; (b)
; (c)
; (d)
图2. 圆柱内切球液晶盒中,+1 boojum缺陷的双轴性局部放大图。(a)
;(b)
;(c)
;(d)
设成与圆柱内切球液晶盒相同的锚定条件,即下基板为强的垂面锚定,上基板为强的沿面锚定。
首先,在
的圆柱形液晶盒中除了在上基板中心处诱导出一个boojum缺陷外,由于液晶盒半径较小还发生了有序重构(图3(a)),这与图2(a)相比具有很大的差异。当
(图3(b))时,在圆柱形液晶盒中诱导出了一个+1 boojum缺陷和一个缺陷环。与图2(b)比较,圆柱形液晶盒内诱导出的boojum缺陷和缺陷环的双轴性都相对较大。当
(图3(c))时,由于到达了与 [15]中临界盒厚相同的尺度条件,圆柱形液晶盒内发生了有序重构现象,而在圆柱内切球液晶盒中只是缺陷环的双轴性变大。继续增大半径,减小盒厚,当
时,如图3(d)所示,由于盒厚足够小圆柱形液晶盒内发生有序重构,而在圆柱内切球液晶盒内没有发生有序重构,只是缺陷环的双轴性变得更大并且沿着球形界面向上扩散(图2(d))。通过对比发现,在强锚定边界条件下,由于球形界面的影响,boojum缺陷结构变小并且有序重构现象消失。

Figure 3. Biaxiality profiles about the structural transition of the +1 boojum in the cylindrical LC cell with the increases of radius and decreases of the cell gap. (a)
; (b)
; (c)
; (d)
图3. 在含有+1缺陷的圆柱形液晶盒内,随着半径的增大和盒厚的减小,以双轴性表征的+1 boojum缺陷的转变过程。(a)
; (b)
; (c)
; (d)
当系统处于平衡态时,在对称轴
处,boojum核心处为负序参数单轴态,其末端为一个各向同性点,这个点称为指尖(finger tip) [6][7];沿着对称轴
向下,指尖下端液晶分子处于正序参数单轴态。下面通过序参数张量Q在对称轴
的本征值图来确定boojum缺陷结构中指尖的位置;随后,通过比较指尖位置的变化情况来表征球形界面对boojum缺陷结构的影响。
图4(a)和图4(b)分别描述了,圆柱内切球液晶盒和圆柱形液晶盒中,
时,序参数张量Q在对称轴
处的本征值图,其中三个本征值相交的地方代表指尖(finger tip)所在的位置
。从图中我们可以看出,在交点的左侧液晶分子处于正序参数单轴态
,而在右侧液晶分子处于负序参数单轴态
。对比图4(a)和图4(b),我们发现图(a)中指尖的位置更靠近球形界面。随着盒厚的增大,两种液晶盒中指尖的位置呈现出一个线性升高的趋势,如图4(c)所示。同时在相同盒厚下,圆柱内切球液晶盒中boojum缺陷结构指尖的位置更靠近球形界面。通过这种现象也可以表征

Figure 4. Profiles about the eigenvalue configurations of the order parameter tensor Q at the symmetry axis
when
. (a) Eigenvalue profiles within the CIS LC cell; (b) Eigenvalue profiles within the cylindrical LC cell. (c) Comparison of the positions of the fingertips in the +1 boojum defect structure in the LC cells of the two models with different cell gaps
图4.
时的序参数张量Q在对称轴
处的本征值图。(a)圆柱内切球液晶盒;(b)圆柱形液晶盒;(c)为在不同盒厚下,这两种模型的液晶盒内+1 boojum缺陷结构中指尖位置的对比图
出,球形界面的影响导致boojum缺陷结构减小。
综上所述,在圆柱内切球液晶盒中,当球形界面设定为强锚定边界条件时,较小的半径R会在球形界面中心处诱导出一个小的+1 boojum缺陷,而圆柱形液晶盒内不仅诱导出了一个boojum缺陷,由于液晶盒半径较小还发生了有序重构。随着半径的增大,在圆柱内切球液晶盒内,除了球形界面上的+1 boojum缺陷之外,还会出现缺陷环,且缺陷环会沿着球形界面向上扩散。而在圆柱形液晶盒中,随着半径的增大,盒厚的减小,首先是有序重构现象消失,只存在一个boojum缺陷;然后继续增大半径,会出现一个缺陷环,最终当
时,由于到达了临界盒厚 [15],缺陷环会发展成新的有序重构。
4.2. 弱锚定边界条件
本节研究球形界面为弱锚定边界条件时,+1 boojum缺陷结构的转变情况。根据文献 [7]中表述,boojum缺陷的出现需要足够强的锚定能,因此,本节中锚定能设置为相对较大的数值。首先,设定锚定强度系数
,约化后的锚定强度系数
。通过研究在不同半径下+1 boojum缺陷的双轴性的局部放大图(图5(a),图5(b))和在对称轴
处的本征值图(图5(c),图5(d))来观察液晶盒内+1 boojum缺陷结构的转变情况。最后通过与相同弱锚定条件下圆柱形液晶盒内的boojum缺陷的结构转变过程进行比较,来探究弱锚定条件下球形界面对+1 boojum缺陷结构形变的影响。
当圆柱内切球液晶盒的半径
时,如图5(a)所示,由于半径较小的原因,导致在球形界面中心处诱导出一个特殊的boojum缺陷,通过观察与之对应的在对称轴
处的本征值图(图5(c))可知,在对称轴上液晶分子一直处于正序参数单轴态,并没有出现指尖结构和负序参数单轴态,且不符合典型的boojum缺陷结构的特征。所以我们将此特殊的boojum缺陷定义为无指尖boojum缺陷。然而,当半径
时(图5(b)),由于锚定强度的原因,球形界面中心处诱导出一个非常小的+1 boojum缺陷和一个缺陷环,此结构与图2(b)中所示结构类似。图5(d)为与图5(b)相对应的对称轴
处的本征值图,从图中

Figure 5. Profiles of biaxiality partial enlargement of the boojum defect in the CIS LC cell and the eigenvalue diagrams of the order parameter tensor Q at the symmetry axis
under the weak anchoring boundary condition when
. (a) and (c)
;(b) and (d)
图5. 在弱锚定边界条件下,锚定强度系数
时,圆柱内切球液晶盒中的boojum缺陷的双轴性局部放大图和序参数张量Q在对称轴
的本征值图。(a)和(c)
;(b)和(d)
我们观察到指尖的位置非常靠近球形界面。
图6为这两种模型的液晶盒中弱锚定条件下+1 boojum缺陷结构的对比,其中图6(a)和图6(b)为圆柱内切球液晶盒中双轴性分布的局部放大图,图6(c)和图6(d)为圆柱形液晶盒中双轴性分布图。当
时,圆柱内切球液晶盒内球形界面中心处诱导出了一个无指尖boojum缺陷(图6(a)),而圆柱形液晶盒中不但在上基板中心处诱导出了一个+1 boojum缺陷,由于半径较小,还出现了有序重构现象(图6(c))。逐渐增大半径、减小盒厚,当
时,在这两种模型内除了诱导出一个+1 boojum缺陷外,由于接近临界盒厚 [15],圆柱形液晶盒内还发生了有序重构(图6(d)),而圆柱内切球液晶盒只出现了一个双轴性较大的缺陷环(图6(b))。
综上,当球形界面及上基板为弱锚定边界条件并且锚定强度系数
时,对于圆柱内切球液晶盒,球形界面会在半径较小(
)时诱导出一个无指尖boojum缺陷,而在圆柱形液晶盒内会发
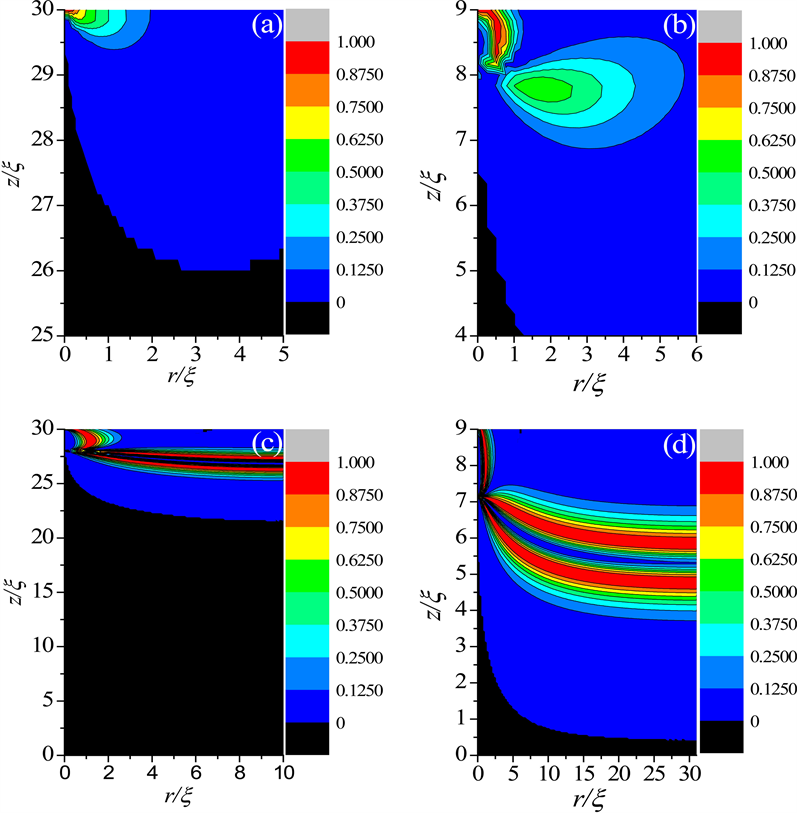
Figure 6. Biaxiality enlargement profiles under the weak anchoring boundary condition when
in two models. (a) and (b) are partial enlarged details of the biaxiality configurations in the CIS LC cell; (c) and (d) are biaxiality configurations in the cylindrical LC cell. In (a) and (c),
; (b) and (d),
图6. 弱锚定边界条件下(
)两种模型的双轴性示意图,(a)和(b)是圆柱内切球液晶盒中的双轴性分布的局部放大图;(c)和(d)是圆柱形液晶盒中的双轴性分布图。(a)和(c)
,(b)和(d)
生有序重构现象。当半径R增大到大约
时,在圆柱内切球液晶盒中,球形界面中心处会诱导出一个非常小的+1 boojum缺陷,并伴随一个缺陷环;而在圆柱形液晶盒中,有序重构现象消失,只存在一个+1 boojum缺陷。继续增大半径,在圆柱内切球液晶盒中缺陷环的双轴性逐渐变大,最终沿着球形界面向上扩散,且不会出现有序重构现象;而在圆柱形液晶盒中,除了+1 boojum缺陷外还会诱导出一个缺陷环,且缺陷环的双轴性逐渐变大。最终,当半径
时缺陷环转变为有序重构。
5. 结论
本文主要研究了含有+1缺陷的纳米级的圆柱内切球液晶盒,其球形界面分别为强、弱两种锚定条件时,界面处诱导的+1 boojum缺陷的结构特征和结构转变情况。随后,在相同锚定条件下,通过与含有+1缺陷的圆柱形液晶盒中的+1 boojum缺陷结构转变过程进行比较,得到球形界面对+1 boojum缺陷形变的影响。
在强锚定边界条件下,对于圆柱内切球液晶盒,球形界面中心处会诱导出一个+1 boojum缺陷。当
时,系统发生结构转变,在液晶盒内出现了一个缺陷环;随着半径的逐渐增大,缺陷环的双轴性逐渐增大,最终会沿着球形界面向上扩散。对于圆柱形液晶盒,当
时,系统发生有序重构。随着半径增大、盒厚减小,有序重构现象逐渐消失,液晶盒内只存在一个+1 boojum缺陷。继续增大半径、减小盒厚,液晶盒内会出现一个缺陷环;当半径
,盒厚
时,缺陷环发展成为新的有序重构现象。
在弱锚定边界条件下,对于圆柱内切球液晶盒,当
时,球形界面上会诱导出一个无指尖boojum缺陷。当半径
时,球形界面中心处会诱导出一个非常小的+1 boojum缺陷和一个缺陷环。然而,对于圆柱形液晶盒,其液晶盒内+1 boojum缺陷的转变过程与强锚定边界条件下的转变过程几乎一致,只是当半径
,盒厚
时,液晶盒内才出现新的有序重构现象。综上,通过对比圆柱内切球液晶盒和圆柱形液晶盒中的+1 boojum缺陷的结构转变过程,可得:在纳米级圆柱内切球液晶盒内,由于球形界面的影响会导致boojum缺陷的结构变小,且不会出现有序重构现象。该现象与球形界面处的强、弱锚定条件无关。
Boojum缺陷在液晶的非显示方面具有重要的应用。例如,利用圆环状胶体在向列相液晶中产生的boojum缺陷实现了新型的二维材料 [30];通过球形胶体在向列相液晶中产生的boojum缺陷捕获了等离子体纳米粒子,并形成新的二聚体单元 [31]等。
致 谢
本课题由国家自然科学基金(11374087, 11447179)支持。作者感谢河北工业大学理学院、电子信息工程学院以及天津市材料器件重点实验室。
基金项目
国家自然科学基金(No.11374087, No.11447179)。
NOTES
*通讯作者。