1. 引言
时空阶梯理论 [1]通过对比研究,发现 [2]星体的运动变化除了受牛顿引力之外,还受能量场和气场的作用力:
。其中,F是能气场力,m是星体质量,E是能量场强度,v是星体的速度,Q
是气感应强度。星体的运动速度是,从牛顿引力看,
,而从能气场力看,
,两等式中的速度与距离的关系正好相反。也就是说,从能气场力看,星系自转曲线随着距离的平方根的增加而增
加,正好抵消了牛顿引力中的随距离的平方根减少的效果。这样,就解决了星系自转问题 [3]。
在宇宙学研究中,哈勃定律成为宇宙膨胀理论的基础,以方程表示:
其中,
是由红移现象测得的星系远离速率,
是哈勃常数,D是星系与观察者之间的距离。
而能气场理论有 [2]:
其中,
是星体的运行速度,而Q是气感应强度,R是星体距离星系中心的距离。
对比
与
,发现唯一的区别就是
中有
项,假如星体运行方向与气场
垂直,
,那么,两个公式就完全相同。所以,哈勃常数对应的是能气场中的气感应强度(或者叫做气场强度也可以,因为这里没有历史的冲突问题。也就是说,气场强度和气感应强度是同一个指标)。
这样,我们就知道了暗能量或者宇宙膨胀原来与气场强度有关。
2. 暗物质问题的有关计算
时空阶梯理论通过对比研究,发现电是能量的压缩版,而磁场是中医气的压缩版,所以,对比电与磁,得出能量与中医气的结论就是:随时间变化的气场可以激发涡旋能量场,随时间变化的能量场可以激发涡旋气场,能量场和气场不是彼此孤立的,它们相互联系、相互激发组成一个统一的能量–气场 [4]。
对比研究揭示 [4]:
1) 能量场是由能量生成。能量线开始于能量收缩态,终止于能量膨胀态。能量收缩态就是原子核状态,能量膨胀态就是暗能量。
2) 气场线没有初始点,也没有终止点。气场线会形成循环或延伸至无穷远。换句话说,进入任何区域的气场线,也必须从那区域离开。通过任意闭曲面的气通量等于零,气场是一个螺线矢量场。
3) 描述随时间变化的气场生成能量场。
4) 气场可以用两种方法生成:一种是靠能量流产生,另一种是靠随时间变化的能量场产生。
既然有了以上的能量场和气场的概念,下面我们就通过对比研究来发现更多的东西:
在电动力学里,洛伦兹力(Lorentz force)是运动于电磁场的带电粒子所受的力。根据洛伦兹力定律,洛伦兹力可以用方程,称为洛伦兹力方程 [5],表达为:
其中,F1是洛伦兹力,q是带电粒子的电荷量,E1是电场强度,v1是带电粒子的速度,B是磁感应强度。
洛伦兹力定律是一个基本公理,不是从别的理论推导出来的定律,而是由多次重复完成的实验所得到的同样的结果。
既然能量场类似电场,气场类似磁场,类似地,我们可以得到能量气场力方程,表达为:
,(可以称之为洛伦兹力能气方程)。
其中,F是能量气场力,m是星体质量,E是能量场强度,v是星体的速度,Q是气感应强度。
若带电粒子射入匀强磁场内,它的速度与磁场间夹角为
,这个粒子将作等距螺旋线运动,螺旋半径,周期和螺距分别为 [5]:
类似地,若星体(m)进入气场内,它的速度与气场间夹角为
,这个星体将作等距螺旋线运动,螺旋半径,周期和螺距分别为:
以上就是气场对于星体运动变化的影响。以上计算,因为在能量气场中,电荷变成了m,所以,可以消去。消去质量m之后,星体的运动速度只与气场和距离有关,而且与距离成正比。
另外,从从牛顿力学可知:
所以,星体运动速度为:
而通过气场计算的星体速度为:
假如两个速度相等,就是两个速度重合,应该是星体稳定的状态,那么得到:
经过变换后得到:
我们从上面的周期公式知道:
所以,
经过变换得到:
等式的右边,假如星体围绕的核心是固定的,那么就是一个常数。这里突然出现了与开普勒第三定律非常类似的公式。以上的推导,我们是从气场对于星体运动变化的影响因素出发,推导出来的。
从万有引力出发,可以推导出开普勒第三定律 [6]:
。
我们可以看出,从气场得出的周期方程与从牛顿引力得出的周期方程只差一个
,而这里的
是星体与气场间的夹角。假如星体与气场的夹角是90˚,而
,我们就可以得到与从
牛顿引力得出的周期方程:
。
从不同的渠道,得出同样的结果,说明以上通过类比得到的公式也是成立的,是对的,而且从气场得出的周期方程更加精细,因为带有
。
星体运动,除了受牛顿引力
之外,还有受能量场和气场导致的引力:
,
这个产生引力的能量场和气场就是我们长期寻找的暗物质。其中,气场与星体的运动速度关系是:
,
是星体的运动速度,
是星体距离核心的距离,
是气感应强度(或者气场强度)。电场强度
等于磁感应强度乘以带电粒子的速度(
),我们就可以类推:气感应强度应该等于能量场强度除
以速度:
,所以,
,变换得到:
。假如星体(m)进入气场内,它的速度
与气场间夹角为九十度,则有
。
我们看到,从牛顿引力看,
,而从能量场和气场看,
,两等式中的速度与距离的
关系正好相反,所以,两者的作用正好抵消了。假如两个速度和距离一样,两个等式相乘,我们得到
,所以,
。从这个等式可以看出,星体的运行速度与距离无关,而是与能量场
强度(E)和核心质量(M)有关。这里核心质量(M)是相对稳定的,唯一的变量就是能量场强度,而能量场强度来自电场强度的类推,所以,计算电场强度的公式一旦代入,发现还是速度平方与距离成反比,但是,电场强度的电荷与能量场强度的能量一对比,我们就发现能量的核心不明显了,所以,距离能量中心的距离,也就有了模糊性,也就是说,能量场强度就不会随着距离的增加而减少。
以上是理论推论,下面我们看看事实观测:哈佛–史密松天体物理中心的研究人员沃克(Matt Walker)发现:暗物质密度是均匀分布在星系中的,中心部位和其它部位的密度几乎一致 [7]。能量场强度,本来就是反映是暗物质密度分布的。既然暗物质是分布均匀的,那么,能量场强度在星系之中就是一个相对不变的量。
星体的运动速度,从牛顿引力看,
,而从能气场看,
。
我们从以上公式可以看出,在牛顿引力下,星体的运动速度(
)与轨道半径R的平方根成反比,而在能气场力下,星体的运动速度(
)与轨道半径R的平方根成正比。
两种力产生两个速度(
和
),我们设星体的最后运行速度是
,假如
,那么,
,假如
,那么,
,其中,
是速度快的一方消失的部分,也是速度慢的一方增加的一方,最后两者趋向最后的稳定速度
,所以,公式中的
都是相等的。
合并计算,我们得到星体的最后运行速度公式:
,也就是说,星体受到牛顿引力和能气场力的共同作用,星体的最后速度就是两种力速度的平均值。
1) 银河系自转曲线的理论计算与实际观测比较
我们首先用太阳的运行速度和银河系的质量算出能量场强度来,因为能量场强度相对不变,我们可以把这个能量场强度当做银河系内的一个常量。
太阳轨道内的银河系的质量是9.56 × 1010太阳质量,太阳的质量M = 1.98855 × 1030 Kg,太阳的轨道速度是220 km/s。
因为
,所以,
,我们代入数值得到银河系内的能量场强度 E = 0.00000000018463112134 m/s2,我们用这个相对固定的数值,计算能气场力的星体速度
,同时我们计算牛顿引力的速度
。
计算得到:
表1是具体的数值,我们看到,从银心开始到周边,牛顿引力导致的星体旋转速度逐渐减小,而能气场力导致的星体旋转速度逐渐增大,两者在8.5 kpc处重合。这个重合的地方,也是太阳系所在的位置。我们同时看到,两力导致的星体的最后速度(就是两力平均速度),在8 kpc和10 kpc之间,居然都在220 km/s左右,相差不到1 km/s。其实,在5 kpc和15 kpc之间,旋转速度的变化只是在220 km/s与228 km/s之间,变化幅度也是非常小的。
图1是理论计算的两力的平均速度曲线,其实就是银河系自转曲线的理论计算曲线,因为两力的平均速度就是星体的最后速度。我们看到,从4 kpc到20 kpc的巨大范围内,曲线基本上是平坦的。
早在20世纪70年代后期 [3],人们已经清楚地意识到,旋涡星系自转曲线在盘的外区通常呈平坦状,即V (R)值大致保持不变,它并不随中心距R的增大而减小 [8][9][10],这一结果随即被用作支持此类星系存在大质量暗物质晕的观测证据 [11]。差不多同一时期,类似的情况在银河系中也得到了确证——在银盘外区,直至R ≈ 15 kpc范围内自转曲线是平坦的,V (R)值甚至略有增大 [11][12]。到20世纪90年代,

Table 1. Star speeds caused by Newton’s gravitational, energy Qi field and resultant forces (Milky Way)
表1. 牛顿引力和能气场力以及合力导致的星体速度(银河系)

Figure 1. The theoretical rotation curve of the milky way
图1. 理论计算的银河系旋转曲线
关于银河系自转曲线的观测研究,所涉及示踪天体的银心距至少已达到R ≈ 21.25 kpc [13][14],而在这一范围内上述基本结论仍然成立。
1983年 [3],Schneider和Terzian [15]利用Schneider等人 [16]所提供的524个PN,对其中有距离测定值的250个PN做了一项研究,样本银心距范围4 < R < 19 kpc。他们发现V太阳 ≈ 220 km/s,而当R > 8.5 kpc时自转曲线有所抬高;不过,远银心距PN转动速度的不确 定性相当大(参见文献 [15]之图2)。后来的一些研究表明,自R = 8.5 kpc起外盘的自转曲线基本上是平坦的,V (R)值并未表现出有明显增大或减小的趋势 [17][18][19];这些工作所用的样本PN,尽管个数有的已接近900 [18],但银心距均不超过14 kpc。
以上的观测数据,在R ≈ 15 kpc范围内自转曲线是平坦的,而理论计算,在R ≈ 15 kpc范围内,自转曲线是平坦的,尤其在6 < R < 12 kpc的范围内,速度基本相等,都在220 km/s左右,浮动很小。在更大的范围内,距离银心在4 < R < 19 kpc,V太阳 = 220.0000076 km/s,而当R > 8.5 kpc时自转曲线有所抬高,这个有所提高,理论计算的结果就是从R = 8.5 kpc时的220 km/s提高到R = 19 kpc时的238 km/s。
通过以上对比,我们得出的结论就是:银河系自转曲线的理论计算和实际观测基本吻合。我们也可以解释为什么:在很大距离范围内的恒星和气体都以每秒大约220公里的速度在轨道上绕着银河中心运行 [19]。因为从图一我们可以看出,在距离银心的8 kpc,9 kpc,10 kpc范围内,速度都在v = 220 km/s附近,差距不超过1 km/s,所以我们观测到在很大距离范围内的恒星和气体都以每秒大约220公里的速度在轨道上绕着银河中心运行。
2) 仙女座星系(M31)自转曲线的理论计算与实际观测比较
我们首先利用大部分的星体的运行速度226 km/s,和
,计算出速度在226 km/s的星体轨道
以内的仙女座星系的质量:2.668348638 × 1011太阳质量。太阳的质量M = 1.98855 × 1030 Kg。
因为,
,我们代入数值得到仙女座星系内的能量场强度E (M31) = 0.0000000000736654
m/s2,我们用这个相对固定的数值,计算能气场力的星体速度
,同时我们计算牛顿引力的速度
。
计算得到:
表2是具体的数值(其中实际观测速度(km/s)来自 [20]),我们看到,从中心开始到周边,牛顿引力导致的星体旋转速度逐渐减小,而能气场力导致的星体旋转速度逐渐增大,两者在22.47 kpc处重合。我们同时看到,两力导致的星体的最后速度(就是两力平均速度),在19.3 kpc和26.56 kpc之间,居然都在226 km/s左右,相差不到1 km/s。其实,在11.35 kpc和34.73 kpc之间,旋转速度的变化只是在226 km/s与239 km/s之间,变化幅度也是非常小的。
从图2可以知道,理论计算的两力的平均速度曲线(其实就是星体的最后速度,就是理论预测速度),与实际观测曲线 [20],基本重合。但是,两种力导致的各自的速度与实际观测曲线还是有一定的差距的。
通过以上对比,我们得出的结论就是:仙女座星系自转曲线的理论计算和实际观测基本吻合。我们也可以解释为什么:在20 < R < 35 kpc范围内,自转曲线基本上是平坦的 [20],因为在19.3 kpc和34.73 kpc之间,旋转速度只是从226.65 km/s升高至231.38 km/s,相差只有4.73 km/s,相差很小,而且在19.3 kpc和26.56 kpc之间,都在226 km/s左右,相差不到1 km/s。所以,在20 < R < 35 kpc范围内,自转曲线基本上是平坦的 [20]。
这里需要注意的是,我们的计算有统一性,就是仙女座星系的质量是统一的,就是仙女座星系的质量

Table 2. Comparison of actual observation speed with theoretical calculation (Andromeda Galaxy)
表2. 实际观测速度与理论计算值对比(仙女座星系)
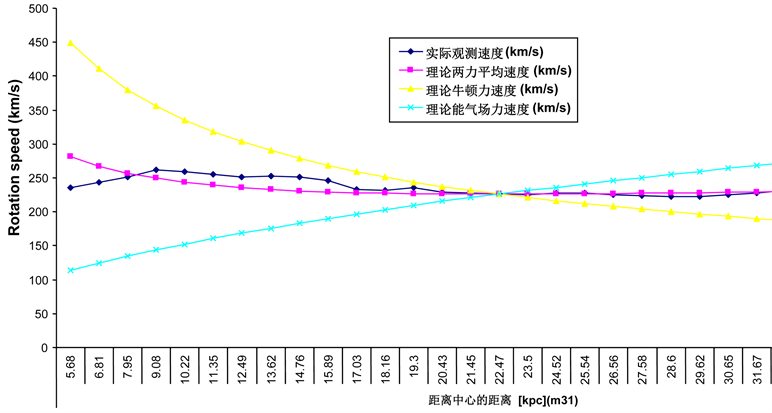
Figure 2. Comparison rotation curve between actual observation and theoretical calculation (M31)
图2. 实际观测与理论计算的对比旋转曲线(M31)
都是:2.668348638 × 1011太阳质量,这个总质量大约是距离中心19.3 kpc以内的质量,但是,这个统一的仙女星座的质量,将影响计算牛顿引力的速度
(
是随着距离中心的距离而变化的,但是
有了这个统一性的计算,
没有变化),也就是说,在距离中心距离的5.68,6.81,7.95 kpc处,这个总质量是偏大的,所以在距离中心的5.68,6.81,7.95 kpc处,理论两力平均速度稍高。
3) NGC 3198星系自转曲线的理论计算与实际观测比较
我们首先利用大部分的星体的运行速度149.3 km/s,和
,计算出速度在149.3 km/s的星体
轨道以内(34.2 kpc)的NGC 3198星系的质量:1.772426943378398107 × 1011太阳质量。太阳的质量M = 1.98855 × 1030 Kg。
因为,
,我们代入数值得到NGC 3198星系内的能量场强度 E (NGC 3198) = 0.0000000000211223854806 m/s2,我们用这个相对固定的数值,计算能气场力的星体速度
,同时我们计算牛顿引力的速度
。
计算得到:
表3是具体的数值(其中实际观测速度(km/s)来自 [21]),我们看到,从中心开始到周边,牛顿引力导致的星体旋转速度逐渐减小,而能气场力导致的星体旋转速度逐渐增大,两者在34.2 kpc处重合。我们同时看到,两力导致的星体的最后速度(就是两力平均速度),在24.1 kpc和48.2 kpc之间,居然都在149 km/s左右,相差不到2.3 km/s。其实,在10.1 kpc和48.2 kpc之间,旋转速度的变化只是在149 km/s与178 km/s之间,变化幅度也是非常小的。
从图3可以知道,理论计算的两力的平均速度曲线(其实就是星体的最后速度,就是理论预测速度),与实际观测曲线 [21],基本重合。但是,两种力导致的各自的速度与实际观测曲线还是有一定的差距的。
通过以上对比,我们得出得出的结论就是:NGC 3198星系自转曲线的理论计算和实际观测基本吻合,尤其在距离中心的10.1 kpc和48.2 kpc之间,几乎完全重合。
与仙女座星系同样的原因,NGC 3198星系的计算有统一性,就是NGC 3198星系的质量是统一的,就是NGC 3198星系的质量都是:1.772426943378398107 × 1011太阳质量,这个总质量大约是距离中心
34.2 kpc以内的质量,这个统一的NGC 3198星系的质量,将影响计算牛顿引力的速度
,也就
是说,在距离中心的2 kpc至12.1 kpc的范围内,这个总质量是偏大的,所以在距离中心的2 kpc至12.1 kpc的范围内,理论两力平均速度稍高。NGC 3198星系的计算的误差比仙女座星系更大,是因为NGC 3198星系的计算从更近中心的距离算起(距离中心2 kpc),而仙女座星系的计算从距离中心的5.68 kpc算起。
需要说明的是,计算有统一性是为了获得这个星系的能量场强度。其实,应该有更精细的计算,就是每一个区域应该有真实的能量场强度和这个区域真实的总质量。假如有一天的观测,得到所有的真实数据,再按照这个理论去计算,应该会得到更好的理论计算与实际观测相吻合的曲线。
3. 暗能量问题的有关计算
在宇宙学研究中,哈勃定律成为宇宙膨胀理论的基础,以方程表示:
(1)
其中,
是由红移现象测得的星系远离速率,
是哈勃常数,D是星系与观察者之间的距离。

Table 3. Comparison of actual observation speed with theoretical calculation
表3. 实际观测速度与理论计算值对比(NGC 3198)

Figure 3. Comparison rotation curve between actual observation and theoretical calculation (NGC 3198)
图3. 实际观测与理论计算的对比旋转曲线(NGC 3198)
而在能气场中,F = m(E +v × Q),
(2)。
对比(1)与(2),发现唯一的区别就是(2)中有
项,假如星体的运行方向与气场方向垂直,
,那么,(1)与(2)公式就完全相同。所以,哈勃常数对应能气场中的气感应强度,或者叫做气场强度也可以,因为这里没有历史的冲突问题。也就是说,气场强度和气感应强度是同一个指标。
能气场力公式F =m(E +v Q)对比牛顿第二定律F = ma,我们就知道(E + v Q)其实就能气场的加速度。其中,E是能量场的收缩加速度,而v Q是气场的收缩加速度。
按照时空阶梯理论,物质加速收缩,暗能量加速膨胀,两者是相反相成的矛盾统一体,所以,暗能量的膨胀加速度与物质的收缩加速度应该是相等的。
既然暗能量的膨胀加速度和物质的收缩加速度相等,那么,又知道暗能量的最低速度就是光速,这样,我们就可以计算出相对应的暗能量的膨胀加速度。
这里需要简述一下时空阶梯理论的有关内容:气时空极化产生形而上的暗能量和形而下的物质,物质是群速度而暗能量是相速度,所以,物质的最高速度是光速,而暗能量的最低速度就是光速。
气场属于暗物质,偏向物质,所以还是属于引力的范畴,属于收缩的范畴,而哈勃常数是属于膨胀的,正好对应气场强度的收缩,两者大小相等,方向相反。
我们知道气场的收缩加速度是:vQ,这个加速度在能气场力公式中:F = m(E +v Q)。
按照气场的收缩加速度公式,又知道哈勃常数与气场强度对应,而暗能量的最低速度是光速,所以我们推知暗能量的膨胀加速度=光速乘以哈勃常数 = cH0。
哈勃常数有两个数值,一个来自欧洲空间局发射的普朗克探测卫星,2015年测量宇宙微波背景辐射,结果得出:哈勃常数为67.74 ± 0.46公里/秒∙百万秒差距(67.74 ± 0.46 km/s/Mpc)。另外一个是诺奖得主研究团队最新研究成果:73.45 ± 1.66公里/秒∙百万秒差距(73.45 ± 1.66 km/s/Mpc) [22]。
下面我们就计算两个暗能量的膨胀加速度:
暗能量的膨胀加速度1 = cH01
=(299792458 m/s × 67740 m/s)/3.086 e + 22 m
=6.58066788882696 × 10−10 m/s2
暗能量的膨胀加速度2 = cH02
=(299792458 m/s × 73450 m/s)/3.086 e + 22 m
=7.13537136749837977965 × 10−10 m/s2
两个暗能量的膨胀加速度的平均值=
6.858019628162669889825 × 10−10 m/s2
先驱者号在银河系内的运动,除了受牛顿引力作用之外,也受到能气场力的作用,而能气场力的公式为:F = m(E + v Q),其中,E + v Q就是先驱者号受到的收缩加速度。
我们知道,E就是银河系内能量场强度。
银河系内的能量场强度E = 0.00000000018463112134 m/s2 = 1.8463112134 × 10−10 m/s2
而vQ就是气场收缩加速度,与宇宙膨胀加速度相等,所以,vQ就等于两个暗能量的膨胀加速度的平均值 = 6.858019628162669889825 × 10−10 m/s2
这样,我们就可以得出先驱者号受到能气场力的全部的加速度:
1.8463112134 × 10−10 m/s2 + 6.858019628162669889825 × 10−10 m/s2
=8.704330841562669889825 × 10−10 m/s2。这个是先驱者号的能气场力的加速度,应该算是理论预测值。
下面我们看看,先驱者号的异常加速度的实际计算值:
先驱者号的异常加速度 = (8.74 ± 1.33) × 10−10 m/s2 [23][24][25]。
我们可以看到,先驱者号异常加速度的理论计算值(8.704330841562669889825 × 10−10 m/s2)和实际观测计算值(8.74 ± 1.33 × 10−10 m/s2)基本吻合,都在8.7 × 10−10 m/s2左右。
我们通过时空阶梯理论的收缩和膨胀的对应关系,把气场强度与哈勃常数对应起来,并通过计算宇宙膨胀的加速度,得出相应的气场收缩的加速度,再加上银河系的能量场收缩加速度,得出了先驱者号的异常加速度。这个计算不仅解决了先驱者号异常加速度的问题,也丰富了时空阶梯理论,从计算我们知道,我们测量到的宇宙膨胀,与能气场中的气场相对应,而暗物质的计算与能气场中的能量场相对应,所以,能气场理论把暗物质和暗能量联系到了一起。
另外,以上计算有个关键等式:
宇宙收缩加速度 = 宇宙膨胀加速度。
说明宇宙加速膨胀的同时,宇宙正加速收缩。宇宙加速收缩表现在两个方面:一个是原子的形成,一个是星系的形成。
这个等式具体表达为:vQ = cH0 (v为物体在气场中的运动速度,Q为气场强度,c为光速,H0为哈勃常数。)
变换得到:
我们知道,时空阶梯理论的力的总公式 [26]为:
,其中,
是时空阶梯因子,这个时空阶梯因子,让力从非常弱的牛顿引力一直到非常强的强力。
我们看到,有关宇宙膨胀方面,也出现了类似的时空阶梯因子:
,具体的宇宙膨胀公式,现在还
不知道,但是,这个时空阶梯因子已经出现了。也就是说,力的总公式算是形而下时空逐渐收缩的一个总公式,那么对应的形而上时空的膨胀应该也有一个总公式。
形而下时空的加速收缩表现为不同等级的力,而且这个等级非常巨大,强力是牛顿引力的1038倍 [27]。对应形而上时空的加速膨胀,也应该表现为不同的等级,而且这个等级也应该非常巨大。比较形而下时空的物质研究,形而上时空的暗能量的研究可以说才刚刚起步,但是,只要我们有了这个形而下与形而上时空的对称原则,我们会逐渐把暗能量的神秘面纱慢慢揭开。
4. 暗物质和暗能量问题的综合考虑
以上计算,感觉暗物质的计算,有充足的观测数据,因为现在已经有众多的星系被观测了。计算越多,感觉暗物质的计算越对,也就是说,计算一个星系可能是巧合,但是,假如许多星系都符合的话,证明这种暗物质的计算是对的。而暗能量的计算只有一个先驱者号异常加速度的数据,似乎有些单薄,纯属巧合的可能性是存在的。
但是,暗能量的计算由于来自人类制造的先驱者号,所以,反而在未来,我们会有更多的机会去实验和预测。我们可以再发射类似一些先驱者号宇宙探测器,变换不同的角度,然后再测定这些宇宙探测器的异常加速度。因为能气场力类似洛仑兹力,所以,物体在气场中运动受到的力为:
,其中
是物体运动方向与气场方向的夹角,当物体(宇宙探测器)运动速度方向跟气场强度的方向平行时,物体(宇宙探测器)受到的气场力为零。调整不同的运动方向,我们可以得出不同的宇宙探测器受到的气场力,根据这些数据,我们会逐渐知道气场的方向是如何的,气场强度是多少。这就真正开始了气场的宏大研究。
这里,最起码的一个预测就是:当宇宙探测器变换不同方向,我们获得一些不同的异常加速度的时候,这个理论就已经成功了一半。
时空阶梯理论揭示 [4]:随时间变化的气场可以激发涡旋能量场,随时间变化的能量场可以激发涡旋气场,能量场和气场不是彼此孤立的,它们相互联系、相互激发组成一个统一的能量-气场。暗物质的计算与能量场有关,暗能量的计算与气场有关,而能量场与气场是一个统一的能气场,所以,暗物质和暗能量通过能气场的连接也成为一个不可分离的整体。这个整体就是时空阶梯理论意义上的整体,就是暗物质正在收缩的同时,暗能量正在膨胀。
5. 总结
时空阶梯理论通过对比研究发现了能气场 [4],能气场包含有能量场和气场,我们以能量场为基础,计算出三个星系自转曲线的理论值,这些理论值与实际观测数值基本吻合。我们以气场理论为基础,把哈勃常数作为气场强度的对应值,计算出了先驱者号异常加速度的理论值,与之前的实际计算基本吻合。
这里的关键是,暗物质和暗能量的计算,来自同一理论基础,就是能气场理论,而两者的计算理论值与实际观测值都基本吻合,这证明能气场理论是正确的。
最后需要强调的是,今后我们的研究方向应该是中医气的研究,因为中医气就是暗物质。在小的范围,我们可以在实验室内制造出人工气 [4],在大的范围,我们可以发射宇宙探测器,在整个太阳系内,通过不同的速度和方向的调整,获得一些气场的不同数据,以补充实验室太小的缺陷。两者结合,我们相信,气的研究,或者暗物质的研究,会像电的研究一样,肯定会给人类带来巨大的进步。