线性互补问题模系矩阵分裂迭代方法解的扰动分析

Perturbation Analysis of Solutions for Matrix Splitting Iterative Methods of Linear Complementarity Problems

摘要: 线性互补问题在经济，金融，交通和力学等诸多领域有着广泛的应用。因此如何求解结构矩阵线性互补问题的方法已然成为时下数值计算方面的热门话题。而这类问题往往牵涉到大型稀疏矩阵，对于这类问题的解的扰动分析就更加重要。模系矩阵分裂迭代方法是最近提出的用于求解线性互补问题的一种迭代方法，在实际应用中易于实现且非常有效。本文系统地研究了模系矩阵分裂迭代方法下的线性互补问题解的扰动分析，即当系数矩阵发生扰动时，线性互补问题的解作何变化。

Abstract: Linear complementarity problem has been widely used in many fields, such as economy, finance, transportation and mechanics. Therefore, how to solve the linear complementarity problem of structural matrix has become a hot topic in the field of numerical computation. However, this kind of problem often involves large sparse matrices. Splitting iteration method for modular matrix is used for an iterative method for solving the linear complementarity problem is proposed recently; it is easy to implement and is very effective in practical application. This paper systematically stu-dies the modular matrix splitting iterative method, and discusses the method of the linear com-plementarity problem solution of perturbation analysis, namely when the coefficient matrix occurs when the disturbance, the solution for linear complementary changes.

1. 引言

在工程物理、力学、运筹学和经济等领域中，我们都能寻觅到线性互补问题的影子，互补问题在经济的平衡、非协作竞赛、交通分配等问题中有着广泛的应用。而且它也是线性规划、双矩阵对策、二次规划问题的统一结合。因此，关于线性互补问题的研究既有理论意义，又有应用价值。线性互补问题有很多种数值解法，主要包括直接法和迭代法，直接法因其具备求解速度快以及解的精度高等优点，常用来求解中小型的线性互补问题；而迭代法在计算过程中能保持矩阵的稀疏结构，使用较小的存储空间，求解速度快，和直接法相比具有稳定性和可行性，所以适用于工程应用中出现的大型稀疏线性互补问题。21世纪是计算机发展的高峰时期，很多数学问题都可以通过计算机来解决！这就使得数学在解决科技生产重大实际问题的过程中的作用得到了充分的体现，其研究价值在科学技术发展过程中也越来越显著，其中以计算数学尤为突出。线性互补问题的高效求解与误差分析已然成为时下计算科学重要课题之一，如见文献 [1] - [8] 。

在人们的日常生活中，经济问题，对策论的研究，乃至于数学类的规划问题和工程领域相关的都对线性互补问题理论有大范围的应用。例如，它之于目前的双矩阵对策，空间价格平衡，接触和断裂力学，乃至于障碍和自由边界问题，流体弹性动态润滑问题。均大范围的在应用，如见文献 [9] [10] [11] [12] [13] 。因此，如何有效地求解结构矩阵线性互补问题开始成为计算数学界的一个研究热点。本项目主要研究结构矩目前，求解线性互补问题的方法有很多，但这些算法往往存在一定的局限性，并不能很好地解决实际问题，因此对这些方法的改进是很重要的。

最近几年来，随着对线性互补问题算法研究的不断深入，用迭代法求解线性互补问题的文章层出不穷。此外，许多求解线性互补问题的新算法不断涌现，如多分裂法(亦称为平行迭代算法)，二阶分裂法，自适应内点法，超松弛迭代法和共轭梯度法等等。鉴于矩阵分裂方法在求解线性系统中的广泛应用，很多学者便开始思考求解结构矩阵线性互补问题能否使用矩阵分裂法来求解，因此矩阵分裂思想和矩阵分裂迭代方法求解结构矩阵线性互补问题的思想便应运而生。近些年来，经过学者们的努力，发展出了一些比较强有力的矩阵分裂迭代方法来研究结构矩阵线性互补问题的数值解，并取得了一些丰硕的成果。迄今为止，结构矩阵线性互补问题的模系矩阵分裂迭代方法的课题仍然有很大空间，如，对于不同类型的结构系统矩阵的分裂研究；参数和参数矩阵选取问题的研究等等仍然有待研究。另外，结构矩阵线性互补问题的模系矩阵分裂迭代方法解的扰动分析也是一大研究主题。阵线性互补问题的模系矩阵分裂迭代方法。内容包括：讨论模系矩阵分裂迭代方法解的扰动分析，即当系数矩阵发生扰动时，线性互补问题的解作何变化。本文旨在促进结构矩阵线性互补问题的模系矩阵分裂迭代方法解的扰动分析研究,为求解结构矩阵线性互补问题提供有效的方法和理论，有着一定的理论和实际意义。

本文主要研究结构矩阵线性互补问题的模系矩阵分裂迭代方法的解的扰动分析。内容包括：讨论模系矩阵分裂迭代方法解的扰动分析，即当系数矩阵发生扰动时，线性互补问题的解作何变化。

对于给定的矩阵 $A\in R^{n\times n}$ 和向量 $q\in R^n$ ，线性互补问题就是要找到一对向量 $z,r\in R^n$ ，使得

$r:=Az+q\ge 0,z\ge 0,z^{\text{T}}\left(Az+q\right)=0$ (1.1)

成立，线性互补问题(1.1)，常简记为 $LCP\left(q,A\right)$ 。其中向量r，z满足互补关系。线性代数中的扰动分析问题，通常指当系数矩阵发生扰动时，原问题的解作何变化？研究线性互补问题解的稳定性是很有必要的。当原始数据的小变化引起解的很大变化时，那么该问题就是病态的或不稳定的；否则，称该问题是良态的或稳定的。

本文结构如下，在第二部分我们给出一些有用的引理和定理。第三部分我们建立模系矩阵分裂迭代方法解的扰动分析，并给出主要结果。在第四部分中，我们作出相关总结。

2. 预备知识

本节我们给出一些基本定义和引理。

2.1. 基本定义

2.1.1. 线性互补问题

线性互补问题 $LCP\left(q,A\right)$ 描述如下：求解满足

$r:=Az+q\ge 0,z\ge 0,z^{\text{T}}\left(Az+q\right)=0$ (1)

的向量 $z,r$ 。其中 $z,r\in R^n$ ， $A\in R^{n\times n}$ 是实矩阵， $q\in R^n$ 是实向量， $z^{\text{T}}$ 表示向量z的转置矩阵。

2.1.2. Z-矩阵，M-矩阵，H-矩阵

给定方阵 $A=\left(a_{\left(ij\right)}\right)\in R^{\left(n\times n\right)}$ ，其比较矩阵 $\langle A\rangle =\left(\langle a_{ij}\rangle \right)\in R^{n\times n}$ 定义为

$\langle a_{\left(ij\right)}\rangle =\{\begin{array}{l}\left|a_{ij}\right|,i=j,\\ -\left|a_{ij}\right|,i\ne j,\end{array}i,j=1,2,\cdots ,n$

如果方阵A对于所有的 $i\ne j$ 都有 $a_{\left(ij\right)}\le 0$ ，则称其为Z-矩阵，给定非奇异方阵A，如果A是Z-矩阵且 $A^{\left(-1\right)}\ge 0$ ，则称其为M-矩阵；如果它的比较矩阵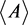是M-矩阵；则称其为H-矩阵；特别地，如果一个H-矩阵的对角元素都是正的，则记为 $H_{+}$ -矩阵。设 $A=M-N$ ，如果M是非奇异的，则称其为A的一个分裂，对于 $A=M-N$ ，如果 $\langle A\rangle =\langle M\rangle -\left|N\right|$ ，则称其为H-相容分裂。若A为 $H_{+}$ -矩阵或者正定矩阵，则对任意的向量q， $LCP\left(q,A\right)$ 都存在唯一解。

2.1.3. 多分裂迭代法

设 $\mathcal{l}$ 是一个正向量， $\mathcal{l}\le n$ ， $A=M_k-N_k,k=1,2,\cdots ,\mathcal{l}$ 是系数矩阵A的一个多分裂， $E_k\in R^{n\times n},k=1,2,\cdots ,n$ 是非负对角矩阵满足 ${\displaystyle \underset{k=1}{\overset{l}{\sum }}{E}_k}=I$ (单位矩阵)，那么三元组集 $\left(M_k,N_k,E_k\right),\left(k=1,2,\cdots ,\mathcal{l}\right)$ 就称为矩阵A的一个多分裂，矩阵 $E_k\left(k=1,2,\cdots ,k\right)$ 称为权重矩阵，给定正对角矩阵为 $\Omega$ ，正常量为 $\gamma$ ，由引理2.3，我们能直接得到：

如果x满足隐式不动点方程

$\left(\Omega +M_k\right)x=N_{k}x+\left(\Omega -A\right)\left|x\right|-\gamma q,k=1,2,\cdots ,\mathcal{l}$ (2)

有

$z={\gamma }^{-1}\left(\left|x\right|+x\right),r={\gamma }^{-1}\Omega \left(\left|x\right|-x\right)$ (3)

是线性互补问题 $LCP\left(q,A\right)$ 的一个解。

2.1.4. 模系矩阵同步多分裂迭代方法

$Lcp\left(q,A\right)$ 的MSM迭代方法(线性互补问题的模系同步多分裂迭代方法)：

定义：设 $A\in R^{n\times n}$ ， $l\left(l\le n\right)$ 是正整数，如果对于 $k=1,2,\cdots ,l$ ， $A=M_K-N_K$ 是矩阵A的分裂矩阵， $E_K\in R^{n\times n}$ 是非负对角矩阵且满足 ${\displaystyle \underset{k=1}{\overset{l}{\sum }}{E}_k}=I$ (单位矩阵)，则称 $\left(M_K,N_K,E_K\right)\left(k=1,2,\cdots ,l\right)$ 是矩阵A的一个多分裂，其中，非对角矩阵 $E_K$ 称为权重矩阵。

设 $\left(M_K,N_K,E_K\right)\left(k=1,2,\cdots ,l\right)$ 是矩阵A的一个多分裂，对于给定正定矩阵 $\Omega$ 和正定常数 $\gamma$ ，由模系

矩阵的收敛性定理可知，如果x满足每一个不动点方程组

$\left(\Omega +M_K\right)x=N_{x}x+\left(\Omega -A\right)\left|x\right|-\gamma q,k=1,2,\cdots ,l$ (4)

那么

$\text{z}=\frac{1}{\gamma }\left(\left|x\right|+x\right),r=\frac{1}{\gamma }\Omega \left(\left|x\right|-x\right)$

是 $LCP\left(q,A\right)$ 的一个解。

根据 $LCP\left(q,A\right)$ 的等价形式，我们称这个为模系同步多分裂迭代方法，简称为MSM迭代方法。

2.1.5. 矩阵奇异值

矩阵A的奇异值记为 $\sigma \left(A\right)$ ， $\sigma \left(A\right)=\sqrt{\lambda \left(A^{\prime }A\right)}$ ， $\lambda \left(A^{\prime }A\right)$ 为 $A^{\prime }A$ 的特征值， $A^{\prime }$ 为矩阵A的共轭转置矩阵。 ${\sigma }_{\text{min}}\left(A\right)$ 为矩阵A的最小奇异值。

2.1.6. 2-范数

矩阵A的2范数就是A的转置矩阵与矩阵A的积的最大特征根的平方根值，是指空间上两个向量矩阵的直线距离。类似于求棋盘上两点间的直线距离。

${\Vert A\Vert }_2$ = A的最大奇异值 = ${\left(\max \left\{{\lambda }_i\left(A^{\prime }A\right)\right\}\right)}^{\frac{1}{2}}$ (欧几里德范数，谱范数，即 $A^{\prime }A$ 特征值 ${\lambda }_i$ 中最大者 ${\lambda }_1$ 的平方根，其中 $A^{\prime }$ 为A的转置共轭矩阵)。

2.2. 引理

设 $A\in R^{n\times n}$ 是 $H_{+}$ -矩阵， $D=diag\left(A\right),B=D-A$ ， $\left(M_k,N_k,E_k\right),\left(k=1,2,\cdots ,\mathcal{l}\right)$ ， $\left(D-L_k,U_k,E_k\right)\left(k=1,2,\cdots ,\mathcal{l}\right)$ 是矩阵A的一个多分裂和三角分裂，明显地，假设 $\gamma >0$ 且正对角矩阵 $\Omega$ 满足 $\Omega >D$

设 $A=M_k-N_k\left(k=1,2,\cdots \mathcal{l}\right)$ 是H-的一个相容分裂，有MSM的迭代序列 ${\left\{z^{\left(m\right)}\right\}}_{m=0}^{\infty }$ 对线性互补问题 $LCP\left(q,A\right)$ 有唯一解， $z_{*}$ 对任意的初始化向量 $z^{\left(0\right)}\in R_{+}^n$ 成立。

证明：对于MSM迭代法有：

$\left(\Omega +M_k\right)x_{\text{*}}=N_k{x}_{\text{*}}+\left(\Omega -A\right)\left|x_{\text{*}}\right|-\gamma q,k=1,2,\cdots ,\mathcal{l}$ (5)

(4)，(5)推出

$x^{\left(m,k\right)}-x_{*}={\left(\Omega +M_k\right)}^{-1}\left[N_k\left(x^{\left(m\right)}-x_{*}\right)+\left(\Omega -A\right)\left(\left|x^{\left(m\right)}\right|-\left|x_{*}\right|\right)\right]$

得出关于MSM迭代法的误差如下

(6)

我们证明(1)的有效性。设 $A=M_k-N_k\left(k=1,2,\cdots ,\mathcal{l}\right)$ 是矩阵A的H+矩阵的H-相容矩阵 $\Omega$ 是一个正对角矩阵， $M_k$ ，因此， $\Omega +M_k,k=1,2,\cdots ,\mathcal{l}$ 是 $H_{+}$ -有

$\left|{\left(\Omega +M_k\right)}^{-1}\right|\le {\langle \Omega +M_k\rangle }^{-1}={\left(\Omega +\langle M_k\rangle \right)}^{-1},k=1,2,\cdots ,\mathcal{l}$ , (7)

(6)两边取绝对值，利用(10)估计不等式 $\left|\left|x^{\left(m\right)}\right|-\left|x_{*}\right|\right|\le \left|x^{\left(m\right)}-x_{*}\right|$ ，相似地，我们可以得到

$\left|x^{\left(m+1\right)}-x_{*}\right|\le {\displaystyle \underset{k=1}{\overset{\mathcal{l}}{\sum }}{E}_k}{\left(\Omega +\langle M_k\rangle \right)}^{-1}\left(\left|N_k\right|+\left|\Omega -A\right|\right)\left|x^{\left(m\right)}-x_{*}\right|:=L_{MSM}\left|x^{\left(m\right)}-x_{*}\right|$ , (8)

其中

$L_{MSM}={\displaystyle \underset{k=1}{\overset{\mathcal{l}}{\sum }}{E}_k}{\left(\Omega +\langle M_k\rangle \right)}^{-1}\left(\left|N_k\right|+\left|\Omega -A\right|\right)$ . (9)

又设 $A=M_k-N_k\left(k=1,2,\cdots ,\mathcal{l}\right)$ 是H-相容分裂也即

$\langle A\rangle =\langle M_k\rangle -\left|N_k\right|,k=1,2,\cdots ,\mathcal{l}$ ，又 $k=1,2,\cdots ,\mathcal{l}$ 有

$\left|N_k\right|=\langle M_k\rangle -\langle A\rangle =\langle M_k\rangle -D-\left|B\right|$ . (10)

由(9)，(10)得出

$\begin{array}{c}{L}_{MSM}={\displaystyle \underset{k=1}{\overset{\mathcal{l}}{\sum }}{E}_k}{\left(\Omega +\langle M_k\rangle \right)}^{-1}\left(\left|N_k\right|+\left(\Omega -D\right)+\left|B\right|\right)\\ ={\displaystyle \underset{k=1}{\overset{\mathcal{l}}{\sum }}{E}_k}{\left(\Omega +\langle M_k\rangle \right)}^{-1}\left[\left(\Omega +\langle M_k\rangle \right)\left(\left|N_k\right|+\left(\Omega -D\right)+\left|B\right|\right)\right]\\ =I-2{\displaystyle \underset{k=1}{\overset{\mathcal{l}}{\sum }}{E}_k}{\left(\Omega +\langle M_k\rangle \right)}^{-1}D\left(I-J\right)\\ \le I-2{\displaystyle \underset{k=1}{\overset{\mathcal{l}}{\sum }}{E}_k}{\left(\Omega +\langle M_k\rangle \right)}^{-1}D\left(I-J_{\epsilon }\right)\end{array}$

则

$\begin{array}{c}{L}_{MSM}{V}_{\epsilon }\le V_{\epsilon }-2{\displaystyle \underset{k=1}{\overset{\mathcal{l}}{\sum }}{E}_k}{\left(\Omega +\langle M_k\rangle \right)}^{-1}D\left(I-J_{\epsilon }\right)V_{\epsilon }\\ =V_{\epsilon }-2\left(1-{\rho }_{\epsilon }\right){\displaystyle \underset{k=1}{\overset{\mathcal{l}}{\sum }}{E}_k}{\left(\Omega +\langle M_k\rangle \right)}^{-1}D{V}_{\epsilon }\end{array}$ (11)

设 $D_k=diag\left(M_k\right),k=1,2,\cdots ,\mathcal{l}$ ，因为 $D_k\left(k=1,2,\cdots ,\mathcal{l}\right)$ 且 $\Omega$ 是一个正对角矩阵，有

${\left(\Omega +\langle M_k\rangle \right)}^{-1}\ge \left(\Omega +D_k\right),k=1,2,\cdots ,\mathcal{l}$ (12)

且

${\displaystyle \underset{k=1}{\overset{\mathcal{l}}{\sum }}{E}_k}{\left(\Omega +D_k\right)}^{-1}>0$ . (13)

当 ${\rho }_{\epsilon }<1$ 时，(11)-((12)+(13))得

$L_{MSM}{V}_{\epsilon }\le V_{\epsilon }-2\left(1-{\rho }_{\epsilon }\right){\displaystyle \underset{k=1}{\overset{\mathcal{l}}{\sum }}{E}_k}{\left(\Omega +\langle M_k\rangle \right)}^{-1}D{V}_{\epsilon }<V_{\epsilon }$ .

因此， $\rho \left(L_{MSM}\right)<1$ 由(9) (11)我们能立即得到MSM迭代法得到的序列 ${\left\{z^{\left(m\right)}\right\}}_{m=0}^{\infty }$ ，对任意的初始向量 $z^{\left(0\right)}\in R_{+}^n$ 线性互补问题 $LCP\left(q,A\right)$ 有唯一解。

$A\in R^{n\times n}$ 是一个H-矩阵， $D=diag\left(A\right)$ 是A的一个对角矩阵， $B=D-A$ ，那么可以得到

(i) A是非奇异的,

(ii) $\left|A^{-1}\right|\le {\langle A\rangle }^{-1}$ ,

(iii) $\left|D\right|$ 是非奇异， $\rho \left({\left|D\right|}^{-1}\left|B\right|\right)<1$ 。

如果系数矩阵 $A\in R^{n\times n}$ 是 $H_{+}$ -矩阵，线性互补问题 $LCP\left(q,A\right)$ 有唯一解，

3. 主要结果

定理3.1 我们定义 $r=Az+q$ ，又 $A=M-N$ ，有 $r=\left(M-N\right)z+q$ 。令r，A，Z，q的扰动分别为 $\Delta r$ ， $\Delta A$ ， $\Delta Z$ ， $\Delta q$ 。设 ${\Vert \Delta r\Vert }_2\le {\delta }_1,{\Vert \Delta M\Vert }_2\le {\delta }_{2M},{\Vert \Delta N\Vert }_2\le {\delta }_{2N},{\Vert \Delta q\Vert }_2\le {\delta }_3$ ，若 ${\delta }_{2M}+{\delta }_{2N}\le {\delta }_{\min }\left(A\right)$ ，则有

${\Vert \Delta Z\Vert }_2\le \frac{{\delta }_1+\left({\delta }_{2M}+{\delta }_{2N}\right){\Vert Z\Vert }_2+{\delta }_3}{{\delta }_{\text{min}}\left(A\right)-\left({\delta }_{2M}+{\delta }_{2N}\right)}$ ,

其中 ${\sigma }_{\text{min}}\left(A\right)$ 是A的最小奇异值。

$r+\Delta r=\left(M+\Delta M-N-\Delta N\right)\left(Z+\Delta Z\right)+q+\Delta q$ (3.1)

由于 $\Delta r=\left(M-N\right)Z+q$ ，那么(3.1)可转化为

$\Delta r=\left(\Delta M-\Delta N\right)Z+\left(M-N\right)\Delta Z+\left(\Delta M-\Delta N\right)\Delta Z+\Delta q$ (3.2)

得

$\Delta Z={\left(M-N\right)}^{-1}\Delta r-{\left(M-N\right)}^{-1}\left(\Delta M-\Delta N\right)Z-{\left(M-N\right)}^{-1}\left(\Delta M-\Delta N\right)\Delta Z-{\left(M-N\right)}^{-1}\Delta q$ (3.3)

由条件 ${\Vert \Delta r\Vert }_2\le {\delta }_1,{\Vert \Delta M\Vert }_2\le {\delta }_{2M},{\Vert \Delta N\Vert }_2\le {\delta }_{2N},{\Vert \Delta q\Vert }_2\le {\delta }_3$ ， $A=M-N$ 可逆，则由(3.3)可得

${\Vert \Delta Z\Vert }_2\le {\Vert A^{-1}\Delta r\Vert }_2+{\Vert A^{-1}\left(\Delta M-\Delta N\right)Z\Vert }_2+{\Vert A^{-1}\left(\Delta M-\Delta N\right)\Delta Z\Vert }_2+{\Vert A^{-1}\Delta q\Vert }_2$ ,

则

${\Vert \Delta Z\Vert }_2\le {\Vert A^{-1}\Vert }_2{\delta }_1+{\Vert A^{-1}\Vert }_2\left({\delta }_{2M}+{\delta }_{2N}\right){\Vert Z\Vert }_2+{\Vert A^{-1}\Vert }_2\left({\delta }_{2M}+{\delta }_{2N}\right){\Vert \Delta Z\Vert }_2+{\Vert A^{-1}\Vert }_2{\delta }_3$

若 ${\delta }_{2M}+{\delta }_{2N}\le {\delta }_{\min }\left(A\right)$ 时，则

${\Vert \Delta Z\Vert }_2\le \frac{{\Vert A^{-1}\Vert }_2\left({\delta }_1+\left({\delta }_{2M}+{\delta }_{2N}\right){\Vert Z\Vert }_2+{\delta }_3\right)}{1-{\Vert A^{-1}\Vert }_2\left({\delta }_{2M}+{\delta }_{2N}\right)}={\Vert \Delta Z\Vert }_2\le \frac{{\delta }_1+\left({\delta }_{2M}+{\delta }_{2N}\right){\Vert Z\Vert }_2+{\delta }_3}{{\delta }_{\text{min}}\left(A\right)-\left({\delta }_{2M}+{\delta }_{2N}\right)}$ .

证毕。

注记：定理3.1给出了模系矩阵分裂迭代方法解Z的误差的上界。

4. 总结

在凸二次优化问题中寻找纳什均衡点，运动的刚体单边约束，不平等的最优控制问题，流体力学中的自由边界问题一系列问题中我们都能看到线性互补问题的应用实例。而这一类问题往往牵涉到大型稀疏矩阵，因此，如何有效地求解这一类矩阵的线性互补问题开始成为计算数学界的一个研究热点。对于大型稀疏矩阵来说，研究它的解的扰动分析显然尤为重要，即分析当系数矩阵发生扰动时线性互补问题的解将做如何变化十分重要，本文就是研究线性互补问题模系矩阵分裂迭代法解的扰动分析。即，定理

(3.1)给出了 $LCP\left(q,A\right)$ 解的误差界 ${\Vert \Delta Z\Vert }_2$ ，根据 $\Delta r,\Delta M,\Delta N,\Delta Z,\Delta q$ 。当 $r,A\left(M-N\right),Z,q$ 存在较小误 $\Delta r,\Delta A,\Delta Z,\Delta q$ 时，可以通过 $\Delta r,\Delta A,\Delta Z,\Delta q$ 求出解的误差界。