1. 引言
光通信作为当代通信技术发展的最新成就,正在逐渐走向广泛应用的道路。1982年德国科研人员A Neyer和E Voges首次提出了光电混合的光电振荡器的概念和构想 [1] ,并进行了初步的实验分析。但是由于长光纤对温度的高度敏感性,导致射频信号频稳性差,近几十年来研究员提出许多改善OEO性能的方法,如注入锁定OEO、双环路OEO [2] 、耦合式OEO [3] 等。2015年,Qu等人实验了光纤布拉格光栅和法布里珀罗滤波器搭建的新型OEO,获得低相噪信号并提高了频率稳定性 [4] 。2016年Tae Hyum Kim等人提出使用光延迟线的OEO,利用声光调制器作为储能元件,证实了可以用很短的环路长度获得较低相位噪声的信号 [5] 。
本文分析了基于注入锁定技术和锁相环技术的光电振荡器,给出了各自的相位噪声模型,为了解决长光纤易受环境温度影响出现的失锁问题,将OEO输出信号和外部参考源信号注入鉴相器,鉴相器输出的直流电压调节延迟线长度,使OEO保持锁相或锁定状态而不失锁,提高OEO的长期稳定性。
2. 注入锁定
2.1. 自注入锁定
自注入锁定(SIL)是提高振荡器的频率稳定度和降低相位噪声的一种很有效的方法 [6] 。通过引出部分信号进行延迟再注入回振荡环路中,可以实现振荡器的自注入锁定。在一定的条件下,采用自注入锁定技术可以使振荡器获得与延迟量成正比的相噪抑制,并增大振荡器的等效Q值,有利于减小振荡器的频率波动。
自注入锁定的框图如图1所示,引出的部分振荡信号经过时间延迟
后以注入强度
反馈进入振荡回路,图中
为输出信号的相位,
,
是注入强度,
是振荡器的3 dB带宽。
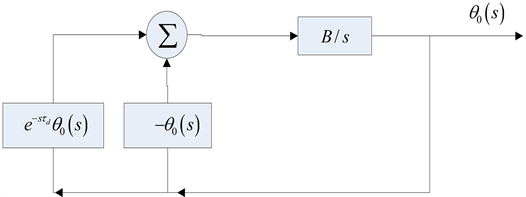
Figure 1. Self-injection locked oscillator block diagram
图1. 自注入锁定振荡器框图
由剩余噪声
引起的输出为:
(1)
由振荡器自身相位噪声
引起的输出为:
(2)
的功率谱密度可以表示为:
(3)
其中
(4)
(5)
为频偏
处的剩余噪声:
(6)
为振荡器在频偏
处的相位噪声 [7] :
(7)
下面根据公式进行Matlab仿真,OEO的光纤环长选为150 m,光纤延迟线分别使用7 km和11 km来进行自注入锁定。仿真后的结果如图2所示,采用自注入锁定使OEO的相位噪声在频偏10 kHz处降低了20 dB左右,相位噪声下降速度也比原先略快。且从图中可以看出,在相同的注入强度下,光纤延迟线越长,OEO的相位噪声抑制量越大。
下面仿真环路长度150 m的OEO采用11 km光纤延迟线在不同注入强度
下的自注入相位噪声曲线图。选取的注入强度系数分别为
,可以清晰的看出在延迟时间
相同的条件下,注入强度
越大,相噪抑制就越好,但是杂散模式噪声的幅值也提高了(图3)。
2.2. 双自注入锁定
双自注入锁定系统的框图如下图4所示,比起上述的自注入锁定,它引出的振荡信号被分为两部分,分别经过
和
的延时并以相同的注入强度
反馈会振荡器。假设两个注入之间没有相互作用,那么双自注入锁定系统的输出是两个注入的叠加。
与自注入锁定的相噪推导公式类似,且假设两路分配的功率相等。
依然有:
(8)
其中
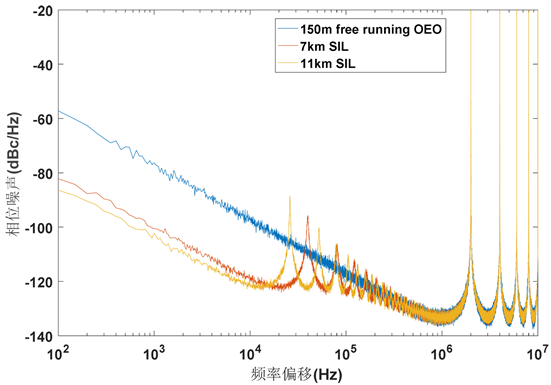
Figure 2. Phase noise simulation of 150 m free running OEO, 7 km SIL OEO and 11 km SIL OEO
图2. 150 m环长自由运行OEO和7 km SIL OEO、11 km SIL OEO的相位噪声仿真
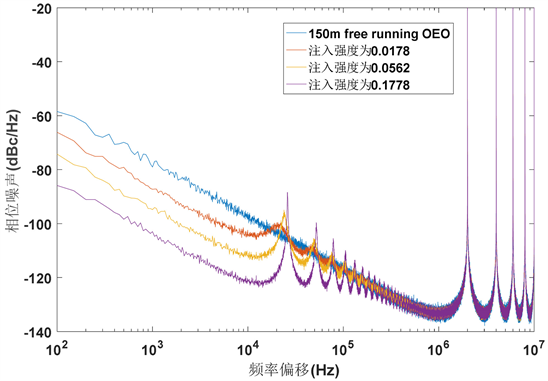
Figure 3. Phase noise simulation of 150 m OEO and 11 km SIL OEO at different injection intensities
图3. 150 m环长OEO和不同注入强度下11 km SIL OEO的相位噪声仿真
(9)
(10)
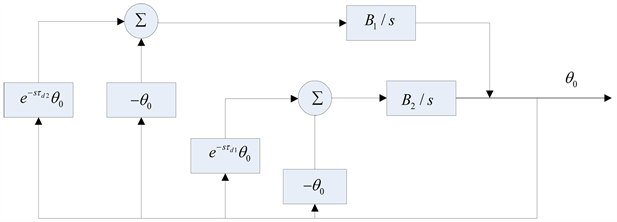
Figure 4. Dual self-injection locked oscillator system block diagram
图4. 双自注入锁定振荡器系统框图
150 m环长OEO采用7 km和11 km光纤延迟线进行双自注入锁定,并单独使用7 km和11 km的光纤延迟线进行自注入锁定,通过matlab仿真对相噪图进行比较。可以看出在双自注入锁定OEO中,杂散模式的抑制较好。双自注入锁定OEO的最好相噪水平决定于其中最长的延迟线的长度以及两个自注入环路的功率分配。本文中两路自注入锁定的功率是相等的,所以双自注入锁定OEO的相噪水平是两段光纤分别进行注入锁定的平均(图5)。
3. 锁相环光电振荡器
锁相环光电振荡器是一种反馈控制系统,可以用来提高OEO的长期稳定性并降低相位噪声。锁相环光电振荡器包括一个外部参考源(External Signal)、鉴相器(Phase Defector)、环路滤波器(Loop Filter)和OEO。锁相环OEO的s域噪声模型如图6所示:
由图6看出锁相环OEO的开环传递函数为:
(11)
其中,
是鉴相因数,
是光电振荡器的控制灵敏度,
是环路滤波器的频响。自由运行的光电振荡器其噪声在锁相环内传输函数为:
(12)
同理,外部参考源的闭环传输函数为:
(13)
鉴相器和环路滤波器的内部噪声闭环传递函数相等为:
(14)
锁相环OEO的输出噪声可以表示为:
(15)
其中
、
、
和
分别表示自由运行OEO、参考源、鉴相器和环路滤波器的相位扰动。
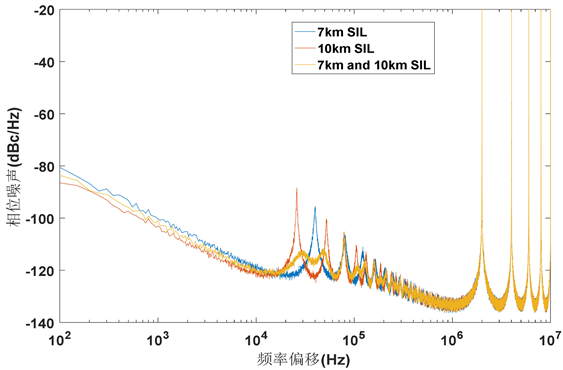
Figure 5. Phase noise comparison between dual self-injection locking and single self-injec- tion-locked OEO
图5. 双自注入锁定与单自注入锁定OEO的相噪对比
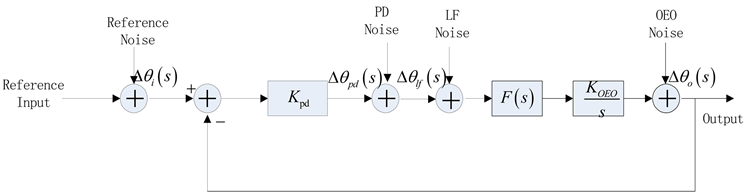
Figure 6. S-domain noise model of phase-locked loop OEO
图6. 锁相环OEO的s域噪声模型
上式表明在锁相环OEO的锁定带宽内,输出信号的相噪更多的受外部参考源、鉴相器和环路滤波器的影响;在锁定带宽外,则受到自由运行光电振荡器自身的影响。因此环路带宽的选择会极大地影响锁相环OEO的相噪,设计滤波器时要综合考虑各个噪声的影响,才能确定锁相带宽。
锁相环OEO最终输出信号的相位噪声在10 kHz处下降了25 dB,而在偏离大于100 kHz的地方没有受到外部信号的影响,锁相环OEO和自由运行的OEO基本保持一致(图7)。
4. 失锁和改进的方法
OEO锁定后的输出频率与参考频率相同,则OEO的频率稳定性由外部参考源的稳定性决定。外部源通常由高稳晶振倍频产生。锁定后稳定性远远优于自由运行的OEO,则希望OEO的锁定带宽能足够的大。但是带宽一味增大会使OEO得相噪性能恶化,所以一般情况下锁定带宽不超过5 kHz,在温度稳定的实验环境下,OEO很容易失锁,一般只能维持几分钟的锁定时间。为了解决该问题本文搭建了锁定状态检测反馈回路,保证OEO频率稳定在锁定频率内。
框图如图8所示,射频衰减器的作用是调节注入强度改变锁定带宽。经过放大后的射频信号被分为
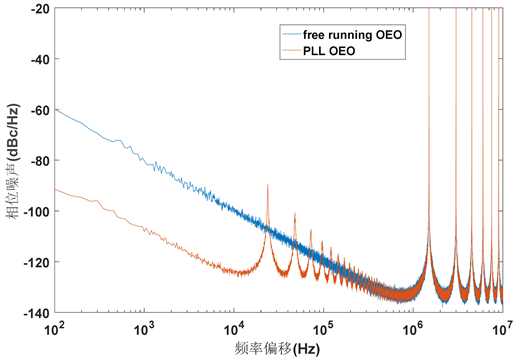
Figure 7. Comparison of phase noise between OEO and phase-locked loop OEO
图7. 自由运行OEO与锁相环OEO相噪比较
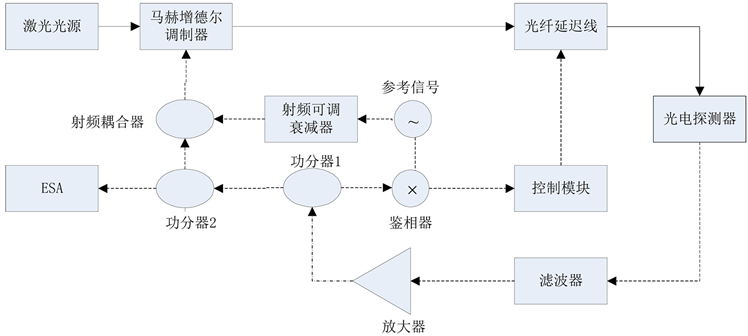
Figure 8. Improved injection-locked photoelectric oscillator structure
图8. 改进的注入锁定式光电振荡器结构图
了三个部分:第一部分耦合后注入马赫增德尔调制器后形成完整的振荡环路;第二部分经过功分后注入鉴相器,鉴相器会输出一个直流电压,大小正比于OEO输出和注入源相位差的正弦函数,控制模块根据直流信号调节延迟线长度,起到监测OEO锁定的情况;第三部分信号用于输出。
5. 窄带带通滤波器
利用ADS优化工具来设计中心频率10 GHz满足要求的窄带滤波器,窄带滤波器电路图如图9所示。
该滤波器3 dB带宽为20 MHz,带内衰减小于3 dB,9.75 GHz处的衰减为−41.747 dB,10.25 GHz处的衰减为−41.921 dB,均小于40 dB;反射系数约为−20 dB。说明该带通滤波器性能良好,满足设计需求(图10)。
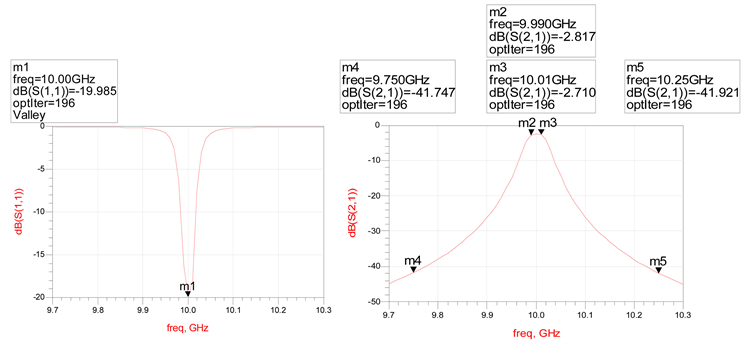
Figure 10. Bandpass filter simulation circuit diagram
图10. 带通滤波器仿真电路图
6. 结论
本文分别仿真分析了基于注入锁定技术和锁相环技术的光电振荡器,理论分析和仿真结果表明锁定后的OEO比自由运行OEO相噪性能优越很多,且延迟线越长、注入强度系数越大则相噪越小。后又针对易失锁的问题提出了改进的注入锁定光电振荡器。保证了自由运行OEO和参考信号间的固有频率差始终处于锁相或锁定带宽内,不发生失所现象。