二维圆盘中不同外场对等离激元激发的影响

Effect of the Different External Fields on Plasmon Excitations in Two-Dimensional Disk

摘要: 基于自由电子气体模型和无规相近似下的线性响应理论，我们研究了二维圆盘中的等离激元。借助能量损耗谱和电荷分布，不同外场对等离激元模式的影响被获得。结果显示：均匀电场只能激发偶极等离激元，而非均匀电场既可激发偶极等离激元，也可激发四极等离激元。

Abstract: We study the plasmon excitations in two-dimensional disk, based on the linear response theory in the random-phase approximation and the free-electron gas model. With the help of energy absorption spectrum and charge distribution, the effect of external electric fields on plasmon is obtained. Results show that the uniform external electric field only can excite quadrupole plasmon; the non-uniform external electric field can excite both quadrupole plasmon and quadrupole plasmon.

1. 引言

早在一百多年前，人们就已发现贵金属纳米颗粒对可见光具有很强的吸收特性。这种现象的本质是费米能级附近导带上的自由电子在电磁场的驱动下在金属表面发生了集体振荡。电子系统的这种集体振荡通常被称为等离激元，它可以被电子激发，也可以被光激发。等离激元被激发时可以产生许多奇异效应，如负折射率现象 [1] [2] 、非线性增强效应 [3] [4] [5] [6] 、远场耦合效应 [7] [8] [9] 、透射增强效应 [10] [11] [12] [13] 等，使其展露出很大的应用潜力。目前，基于等离激元性能的器件研究已经取得了很大的进展。人们发现，利用等离激元可以提高近场显微镜的分辨率、提升二极管的发光效率、实现纳米尺度的电磁场调控以及实现隐身等。

最近，基于自由电子气体模型和无规相近似下的线性响应理论，我们提供了一种研究等离激元的新方法 [14] [15] 。利用这种新方法，我们发现在耦合原子链中，纵向等离激元随原子链长的增大而发生红移，横向等离激元随原子链长的增加而发生蓝移；纵向等离激元的电荷分布成体分布特征，而横向等离激元则分化成了中心模式(电荷主要分布在原子链的中心)和两端模式(电荷主要分布在原子链的两端) [14] 。用新方法得到的这些研究结果和以前人们的研究结果一致，这充分说明了新方法的有效性和正确性。利用新方法，我们还发现了四极等离激元，而四极等离激元在以前的研究中并没有被发现。此外，利用新方法可以获得电子振荡的本征方程，借助电子振荡的本征方程，我们可以获得一个系统所有的等离激元模式，这是新方法的最大优点 [15] 。目前，人们主要通过系统对外界的共振响应来获得系统存在的等离激元模式。这种方法的不足之处是，研究结果易受外场的影响，一些等离激元模式常因没有被激发而没有被发现。但是，利用新方法我们可以获得系统的所有等离激元模式，且结果不受外场影响。

本文中，我们主要把研究等离激元的新方法推广到二维圆盘系统。在圆盘中，电子的本征函数是个复变函数，这导致圆盘中等离激元模式的查找要比耦合原子链中等离激元的查找要复杂的多。本文中，我们采用新方法重点研究不同外场对圆盘内等离激元的激发。

2. 研究方法

由含时密度泛函理论可知，一个系统因外界扰动所产生的诱导电荷密度可以写成

${\rho }^{ind}\left(r,\omega \right)={\displaystyle \int \Pi \left(r,r^{\prime },\omega \right)}V\left(r^{\prime },\omega \right)\text{d}{r}^{\prime }$ (1)

其中 ${\displaystyle \int \Pi \left(r,r^{\prime },\omega \right)}$ 是密度–密度响应函数，在无规则相近似下，其可写为

${\displaystyle \int \Pi \left(r,r^{\prime },\omega \right)}=2e^2{\displaystyle \underset{nm}{\sum }\frac{f\left(E_n\right)-f\left(E_m\right)}{E_n-E_m-\omega -i\gamma }}{\psi }_n^{\ast }\left(r\right){\psi }_m\left(r\right){\psi }_m^{\ast }\left(r^{\prime }\right){\psi }_n\left(r^{\prime }\right)$ (2)

其中， $f\left(E_n\right)$ 是费米分布函数。本文我们只考虑零温情况，在费米能级以下费米分布函数为1，在费米能级以上费米分布函数为0。 ${\psi }_n$ 和 $E_n$ 分别代表系统未受外界扰动时的本征函数和本征能量。 $V$ 为作用于系统的总扰动势，其可看作由外加电势 $V^{ext}$ 和诱导电势 $V^{ind}$ 组成，即 $V=V^{ext}+V^{ind}$ 。

由库伦定律知，诱导电荷在空间产生的电势为

$V^{ind}\left(r,\omega \right)=\frac{1}{4\text{π}{\epsilon }_0}{\displaystyle \int \frac{{\rho }^{ind}\left(r^{\prime },\omega \right)}{\left|r-r^{\prime }\right|}\text{d}{r}^{\prime }}$ (3)

将电荷密度(1)式代入上式，可得

$V^{ind}\left(r,\omega \right)=2e^2{\displaystyle \underset{nm}{\sum }\frac{f\left(E_n\right)-f\left(E_m\right)}{E_n-E_m-\omega -i\gamma }}\times \frac{1}{4\text{π}{\epsilon }_0}{\displaystyle \int \frac{{\psi }_n^{\ast }\left(r^{\prime }\right){\psi }_m\left(r^{\prime }\right)}{\left|r-r^{\prime }\right|}\text{d}{r}^{\prime }}\left[V_{nm}^{ext}\left(\omega \right)+V_{nm}^{ind}\left(\omega \right)\right]$ (4)

其中，

$V_{nm}\left(\omega \right)={\displaystyle \int {\psi }_n^{\ast }}\left(r\right)V\left(r,\omega \right){\psi }_m\left(r\right)$ (5)

在(4)式两边，同乘以 ${\psi }_{n^{\prime }}^{\ast }\left(r\right){\psi }_{m^{\prime }}\left(r\right)$ 并对整个系统积分，可得：

$V_{n^{\prime }{m}^{\prime }}^{ind}\left(\omega \right)=2e^2{\displaystyle \underset{nm}{\sum }\frac{f\left(E_n\right)-f\left(E_m\right)}{E_n-E_m-\omega -i\gamma }}\times \frac{1}{4\text{π}{\epsilon }_0}{\displaystyle \int \frac{{\psi }_n^{\ast }\left(r^{\prime }\right){\psi }_m\left(r^{\prime }\right){\psi }_{n^{\prime }}^{\ast }\left(r\right){\psi }_{m^{\prime }}\left(r\right)}{\left|r-r^{\prime }\right|}}\left[V_{nm}^{ext}\left(\omega \right)+V_{nm}^{ind}\left(\omega \right)\right]\text{d}{r}^{\prime }\text{d}r$ (6)

令

$M_{n^{\prime }{m}^{\prime },nm}\left(\omega \right)=\frac{2e^2}{4\text{π}{\epsilon }_0}{\displaystyle \underset{nm}{\sum }\frac{f\left(E_n\right)-f\left(E_m\right)}{E_n-E_m-\omega -i\gamma }}{\displaystyle \int \frac{{\psi }_{n^{\prime }}^{\ast }\left(r\right){\psi }_{m^{\prime }}\left(r\right){\psi }_n^{\ast }\left(r^{\prime }\right){\psi }_m\left(r^{\prime }\right)}{\left|r-r^{\prime }\right|}}\text{d}{r}^{\prime }\text{d}r$ (7)

则(6)式可写成

${\displaystyle \underset{nm}{\sum }\left[{\delta }_{n^{\prime }{m}^{\prime },nm}-M_{n^{\prime }{m}^{\prime },nm}\left(\omega \right)\right]}{V}_{nm}^{ind}\left(\omega \right)={\displaystyle \underset{nm}{\sum }{M}_{n^{\prime }{m}^{\prime },nm}\left(\omega \right)V_{nm}^{ext}\left(\omega \right)}$ (8)

当外加电场知道时，根据电场和电势的关系 $V^{ext}\left(r,\omega \right)=-{\displaystyle {\int }_r^{r_0}E\left(r,\omega \right)\cdot \text{d}r}$ 可以获得 $V^{ext}\left(\omega \right)$ ( $r_0$ 是电势参考点)，进而利用(5)式可获得 $V_{nm}^{ext}\left(\omega \right)$ 。当 $V_{nm}^{ext}\left(\omega \right)$ 知道时，利用(8)式可获得 $V_{nm}^{ind}\left(\omega \right)$ ，进而利用(1)式可获得诱导电荷密度。

等离激元是电荷的集体振荡，当其激发时会使系统的能量损耗增大，从而导致能量损耗谱中出现损耗峰。因而，我们可以认为能量损耗(Energy absorption)峰所对应的频率就是等离激元的频率。通常情况下，一个系统的能量损耗可以通过下式来计算

$A\left(\omega \right)=-\frac{1}{2}\omega \mathrm{Im}\left\{{\displaystyle \int {\rho }^{ind}\left(r,\omega \right){\left[V^{ext}\left(r,\omega \right)\right]}^{\ast }}\right\}$ (9)

下面，我们来具体研究半径为 $R$ 的二维圆盘中等离激元的激发，圆盘的模型如图1所示。

在自由电子气体模型下，圆盘内电子的本征函数和本征能量分别为

${\psi }_{nk}\left(r,\theta \right)=\sqrt{\frac{1}{\text{π}{R}_{\text{0}}^{\text{2}}}}\frac{J_n\left(\frac{x_{nk}}{R_{\text{0}}^{\text{2}}}r\right)}{J_{n-1}\left(x_{nk}\right)}{e}^{\pm in\theta }$ (10)

$E_{nk}=\frac{{\hslash }^2{x}_{nk}^2}{2m_e{R}_{\text{0}}^{\text{2}}}$ (11)

这里， $x_{nk}$ 代表 $n$ 阶贝赛尔函数的第 $k$ 个零点， $m_e$ 是电子的质量。在后面的计算中，为了表示方面，电子

Figure 1. The two-dimensional disk model in the external electric field incident

图1. 外电场入射下的二维圆盘模型

的波函数被简写成

${\psi }_{nk}\left(r,\theta \right)=C{R}_n\left(N_{k}r\right)e^{\pm in\theta }$ (12)

这里 $C=\sqrt{1/\text{π}{R}_{\text{0}}^{\text{2}}}$ ， $N_k={x_{nk}/R}_{\text{0}}$ ， $R_n\left(N_{k}r\right)=J_n\left(\frac{x_{nk}}{R_{\text{0}}}r\right)/J_n\left(x_{nk}\right)$ 。将(12)式代入(1)式，并利用电荷密度和

电势的展开式

${\rho }^{ind}\left(r,\theta ,\omega \right)={\displaystyle \underset{m}{\sum }{\rho }_m^{ind}\left(r,\omega \right)e^{im\theta }}$ (13)

$V^{ind}\left(r,\theta ,\omega \right)={\displaystyle \underset{m}{\sum }{V}_m^{ind}\left(r,\omega \right)}{e}^{im\theta }$ (14)

可得

$\begin{array}{c}{\rho }_m^{ind}\left(r,\omega \right)=4\text{π}{e}^2\left[{\displaystyle \underset{nk,k^{\prime }}{\sum }\left(\frac{1}{E_{nk}-E_{\left(n+m\right)k^{\prime }}-\omega -i\gamma }+\frac{1}{E_{nk}-E_{\left(n+m\right)k^{\prime }}+\omega +i\gamma }\right)}\right]\\ \times C^2{R}_n\left(N_{k}r\right)R_{n+m}\left(N_{k^{\prime }}r\right)\left[V_{nk{k}^{\prime }}^{ext}\left(\omega \right)+V_{nk{k}^{\prime }}^{ind}\left(\omega \right)\right]\end{array}$ (15)

$V_m^{ind}\left(r,\omega \right)={\displaystyle \int \frac{r^{\prime }{\rho }_m^{ind}\left(r^{\prime },\omega \right){\text{e}}^{im(\theta -{\theta }^{\prime })}}{4\text{π}{\epsilon }_0\sqrt{r^2+{r^{\prime }}^2-2r{r}^{\prime }\cos \left(\theta -{\theta }^{\prime }\right)}}}\text{d}{r}^{\prime }\text{d}\left(\theta -{\theta }^{\prime }\right)$ (16)

这里

$V_{nk{k}^{\prime }}\left(\omega \right)=C^2{\displaystyle \int r^{\prime }{R}_{n+m}\left(N_{k^{\prime }}{r}^{\prime }\right)}{R}_n\left(N_k{r}^{\prime }\right)V_m\left(r^{\prime },\omega \right)\text{d}{r}^{\prime }$ (17)

将电荷密度(15)式代入电势方程(16)式后，两边同乘以 $C^{2}r{R}_a\left(N_{b}r\right)R_{a+m}\left(N_{b^{\prime }}r\right)$ ，并对 $r$ 积分，则有

${\displaystyle \underset{nk{k}^{\prime }}{\sum }\left[{\delta }_{ab{b}^{\prime }}-M_{ab{b}^{\prime },nk{k}^{\prime }}\left(\omega \right)\right]}{V}_{nk{k}^{\prime }}^{ind}\left(\omega \right)={\displaystyle \underset{nk{k}^{\prime }}{\sum }{M}_{ab{b}^{\prime },nk{k}^{\prime }}\left(\omega \right)}{V}_{nk{k}^{\prime }}^{ext}\left(\omega \right)$ (18)

其中

(19)

将(13)式和(14)式代入(9)式，化简后可获得圆盘系统的能量损耗可写成

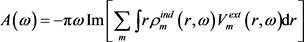(20)

由(14)式可知

(21)

当外加电势已知时，通过(21)式可求得；将代入(17)式，进而可求得；将代入(18)式，可求得。当获得和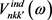后，利用(15)式可获得诱导电荷密度，进而通过(13)式获得等离激元激发时的电荷分布。当和知道后，利用(20)式可获得吸收谱。

3. 结果与分析

在下面的计算结果中，频率ω是以位单位，代表电子的质量，代表金的晶格常数。能量损耗谱和电荷分布分别是通过(13)式和(20)式获得。此外，因本文主要讨论零温情况下金属圆盘内的等离激元激发，所以，圆盘内电子为半填充状态，在费米能级以上费米分布函数为0，在费米能级以下费米分布函数为1。

首先，我们研究了均匀电场(如图1所示)作用下圆盘内等离激元的激发。当等离激元激发时，由于电子的集体振荡，导致系统的能量损耗增加，从而在能量损耗谱中出现损耗峰。我们可以通过损耗峰，来寻找等离激元的频率。图2展示了有损耗峰出现的各频率区间的能量损耗谱，这里。利用损耗峰，四个模式的等离激元被发现，这四个模式的频率分别为：0.363、0.475、0.5786和1.1。

为了对等离激元有更直观的认识，图3给出了等离激元激发时的电荷分布。在图3中，第一排显示的是电荷实部的分布，第二排显示的是电荷的虚部分布。不难发现，电荷的实部分布和虚部分布十分相似，它们只有相位差异。从电荷分布对称性的角度来看，电荷分布相对于y轴(见图1)成对称性分布，电荷分布相对于z轴成反对称分布。因电场关于y轴对称，所以电荷分布关于y轴对称是理所当然的，这并不能反映等离激元特征。所以，在下面的描述中电荷的对称性都是相对于z轴(z轴与电场的对称轴相垂直)而言的，这中电荷分布更能反映出等离激元激发时的电荷分布特征。

接下来，我们研究了非均匀电场作用下等离激元的激发。图4展示了，非均匀电场作用下，有损耗峰出现的各频率区间的能量损耗谱，这里。第一排的四个图，展示了再非均匀电场和均匀电场作用下都可以出现的损耗峰，这四个损耗峰所对应的频率分别为0.363、0.475、0.5786和1.1；第二排的三个峰展示了只有在非均匀电场作用下才可以出现的峰，这些峰对应的频率分别位：0.6592、0.7906、0.8748。

图5展示了均匀电场和非均匀电场都可激发的等离激元(即，图4中第一排的四个损耗峰所对应的等离激元)的电荷分布，这里的电荷分布是在非均匀场的作用下获得的。图5显示电荷分布成反对称性。对比图4和图5可以发现，同一模式的等离激元电荷分布特征并没因外场的变化而改变。

图6展示了，相对于非均匀电场而言，均匀电场未激发的等离激元模式(即，图4中第二排的三个损耗峰所对应的等离激元模式)的电荷分布。从图中，可以清晰的看到这些电荷分布都展现出了对称分布的特征。我们知道对于反对称性的电荷分布是偶极响应存在的标志；而对称性的电荷分布是四极响应存在的标志。这些研究结果说明，像在一维原子链系统一样，均匀电场只能激发圆盘系统的偶极等离激元，而非均匀电场既可激发圆盘系统的偶极等离激元又可激发四极等离激元。

Figure 2. Energy Absorption with frequency in the uniform external electric field

图2. 在均匀电场作用下能量损耗随频率的变化

Figure 3. The charge distribution of the plasmon excited by the uniform electric field

图3. 均匀电场激发的等离激元的电荷分布

Figure 4. Energy absorption with frequency 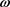in the non-uniform electric field

图4. 在非均匀电场作用下能量损耗随频率的变化

Figure 5. The charge distribution of the plasmon excited by both the uniform field and the non-uniform field

图5. 均匀电场和非均匀电场都能激发的等离激元的电荷分布

Figure 6. The charge distribution of the plasmon excited only by the non-uniform field

图6. 非均匀电场能激发而均匀电场不能激发的等离激元的电荷分布

4. 结论

基于自由电子气体模型和无规相近似下的线性响应理论，我们提供了研究二维圆盘中等离激元模式的方法。结果发现，均匀电场只能激发圆盘中的偶极等离激元，而非均匀电场则既可激发偶极等离激元，又可激发四极等离激元。这些研究结果反映出，在利用系统对外界的共振响应来寻找等离激元时，结果会因一些等离激元没有激发而不能被找到。因而，寻找研究等离激元的新方法是十分有必要的。

基金项目

本文为陕西省科技厅科研项目(2018JQ1091)，西安航空学院校级项目(2017KY0209)和西安航空学院横向项目(规则纳米器件中等离激元的模式及其激发方式研究)的资助课题。

NOTES

^*通讯作者。