1. 引言
表面等离激元是光与金属表面的电子相互作用,形成的一种表面电磁模式,其横向可以实现对电磁场亚波长尺度的束缚,从根本上突破了衍射极限的限制。表面等离激元激发所引起的诸多奇异效应,如透射增强效应 [1] [2] 、局域场强增强效应 [3] [4] 、非线性转换过程增强效应 [5] [6] 、和负折射现象 [7] [8] [9] [10] 等,使其展现出了巨大的应用潜力,吸引了越来越多的科研人员进行这方面的理论和实际应用研究。
Nie发现,Ag纳米颗粒上等离激元激发可使单分子拉曼散射信号的增强因子高达1014,是探测和分析单分子特性的有效工具 [11] 。与单个颗粒的增强效果相比,一对金属纳米颗粒构成的光学天线在等离激元共振激发时会引起电荷的重新分布,并在其缝隙处发生近场耦合,使得该处电场引起的双光子信号增强80倍以上,这为在纳米尺度上调控物质的光物理过程提供了新手段和新技术 [12] 。等离激元产生的非线性光学增强现象可以调控自身在微纳结构中的传播效应。例如,结合等离激元对环境折射率敏感的特性,以及非线性介质的光克尔效应(介质的折射率随光强发生变化),利用控制光场改变非线性介质的折射率,从而改变等离激元的传输特性,这一现象可用于制备亚波长光学电路中的光开关 [13] 。
最近,基于自由电子气体模型和无规相近似下的线性响应理论,在二维矩形原子团簇中,我们提出了研究等离激元的新方法 [14] [15] 。这种方法的优点是,可以找出系统的所有等离激元模式,且结果不受外场影响。本文中,我们把研究等离激元的新方法推广到柱形原子团簇,重点研究横向等离激元和纵向等离激元随柱长的演化。
2. 研究方法
在自由电子气体模型下,方柱(长
,宽
,高
)内电子的本征函数和相应的本征能量分别为
(1)
(2)
这里
。当给方柱一个扰动时,方柱内产生的诱导电荷密度
可以写成
(3)
这里
是密度–密度响应函数,V为作用于系统的总扰动势,其可看做由外加电势
和诱导电势
两部分组成,即
。在无规则相近似下,密度–密度响应函数
可写为
(4)
其中,
是费米分布函数。
和
分别代表系统未受外界扰动时的本征函数和本征能量。
由库伦定律知,诱导电荷
在空间产生的电势为
(5)
将电荷密度(1)式代入(5)式,可得
(6)
其中,
(7)
在(6)式两边,同乘以
并对整个方柱积分,可得:
(8)
令
(9)
则(6)式可写成
(10)
当已知外电场时,由电场和电势的关系可求得电势
;利用(7)式可获得
;利用(10)式可获得
;当
和
都知道后,利用(3)式可获得诱导电荷密度
。
等离激元是电荷的集体振荡,当其激发时会使系统的能量损耗增大,从而导致能量损耗谱中出现损耗峰。因而,我们可以认为能量损耗峰所对应的频率就是等离激元的频率。通常情况下,一个系统的能量损耗可以通过下式来计算 [14]
(11)
3. 结果与分析
在下面的计算结果中,频率
是以
位单位,
代表电子的质量,a = 0.2857 nm代表金的晶格常数。能量吸收谱和电荷分布分别是通过(13)式和(20)式获得。此外,因本文主要讨论零温情况下金属圆盘内的等离激元激发,所以,圆盘内电子为半填充状态,在费米能级以上费米分布函数为0,在费米能级以下费米分布函数为1。
按照习惯,下面我们将平行于方柱轴的电场称为纵向电场(用
表示),其所激发的等离激元称为纵向等离激元(用
表示);将垂直于方柱轴的电场称为横向电场(用
表示),其所激发的等离激元称为横向等离激元(用
表示)。图1显示了纵向等离激元随方柱长度的变化。从峰的移动来看,随着方柱长度的增加,横向等离激圆的频率发生了红移。这种现象主要是因为随着柱长的增加,能级间距减小而引起的。
在图2中,我们展示了横向等离激元随方柱长度的变化。不难发现,横向等离激元有蓝移趋势。对比图1和图2,可以发现纵向等离激元的模式要多于横向等离激元。这主要是因为电子横向运动要比纵向运动更加受限而引起的。
4. 结论
基于自由电子气体模型和无规相近似下的线性响应理论,本文中我们研究了方柱形原子团簇中,
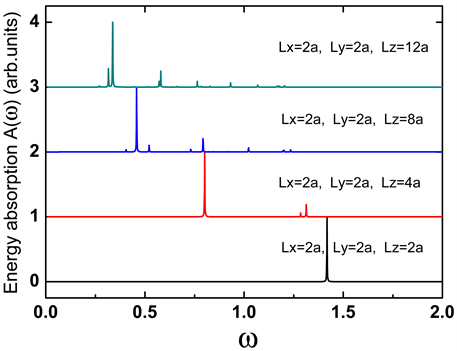
Figure 1. The evolutions of longitudinal plasmon with the length of square cylinder
图1. 横向等离激元随方柱长度的变化

Figure 2. The evolutions of longitudinal plasmon with the length of square cylinder
图2. 纵向等离激元随方柱长度的变化
等离激元随柱长的演化。利用能量吸收谱,等离激元的激发和演化被观测到。结果发现,横向等离激元随柱长的增加而发生蓝移,而纵向等离激元随柱长的增加而发生红移。
基金项目
本文为陕西省科技厅科研项目(2018JQ1091),西安航空学院校级项目(2017KY0209)和西安航空学院横向项目(规则纳米器件中等离激元的模式及其激发方式研究)的资助课题。
NOTES
*通讯作者。