1. 引言
1972年,著名数学家与计算机语言逻辑学家D. Scott引入了连续格的概念 [1] 。后经过多年研究,具有计算机和数学双重背景的连续格理论被推广到使用更广的连续Domain理论 [2] 上,并在一般拓扑学、逻辑学、代数学与计算机逻辑学等基础理论学科的研究上取得了丰硕的研究成果 [3] [4] [5] 。拓扑学与连续Domain理论是密不可分的,作为一般拓扑学的延伸,数学家A.V. Arhangel’skii在文献 [6] 中首次引入相对拓扑的概念,利用相对的思想研究了一般拓扑学。近年来,而作为连续Domain理论的一种量化推广,徐罗山在文献 [7] 中引入相容连续偏序集与定向完备化的概念,从而出现了相容连续Domain理论。受相对拓扑研究思路的启发,作为相容定向集的另一种推广,本文首先利用相对的思想引入相对相容定向集的概念,探讨其基础的性质。然后在相对相容定向完备集基础上给出相对相容小于与相对相容连续偏序集的概念,研究其具有的相关性质给出一些等价刻画。最后证明对于给定的集合T,相对相容双小于同样具有插入性。
2. 预备
本节给出本文所需的基本概念和记号。
设P为偏序集,
,
,记
,对偶地,记
,
,
。
设P为偏序集,
,则X是下集当且仅当
。X为上集当且仅当
。若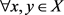 ,
使得
,则称X是P的定向子集;对偶地,可以定义余定向集。设P为偏序集,P称为定向完备偏序集,如果对于P中的每一个定向集D,最小上界
都存在。
,
使得
,则称X是P的定向子集;对偶地,可以定义余定向集。设P为偏序集,P称为定向完备偏序集,如果对于P中的每一个定向集D,最小上界
都存在。
定义2.1 [7] :设P为偏序集,
,
,若D满足:
1) D是定向集,
2) 存在
使得
,则称D为P中的相容定向集。
定义2.2 [7] :设P为偏序集,P称为相容定向完备偏序集,如果对于P中的每一个相容定向集D,
存在。
定义2.3 [7] :设P为相容定向完备偏序集,定义P上的相容way below关系如下:
,对于任意相容定向集D,
存在,若
,则存在
使得
。若
,则称x为相容紧元。用
表示P中所有的相容紧元,记
,
。
定义2.4 [7] :设P为相容定向完备偏序集,称P相容连续(代数)偏序集,若P满足如下条件:
1)
,
(
)为相容定向集,
2)
(
)。
3. 相对相容定向集
作为相容定向集的一种推广,本节引入相对相容定向集和相对相容定向完备集的概念。
定义3.1:设P为偏序集,
,且
,若D满足:
1) D是定向集,
2) 存在
使得
,则称D为P的相对于T的相容定向集。当T明了时,可简称为相对相容定向集。记
= {
:D为P的相对T的相容定向集}。
命题3.2:相对相容定向集必为相容定向集。
证明:
,
,若
,则
使得
,又D本身定向,由相容定向集定义知,D为相容定向集。
注3.3:相容定向集未必是相对相容定向集。
例3.4:如图1所示。
设
,
,令
,易知D为P1中相容定向集,但在给定的集合T中,找不到一个t使得
成立,故D不为P1中相对T相容定向集。
命题3.5:设P为偏序集,
,且
。若
,则D为相对相容定向集当且仅当D为相容定向集。
下面利用相对相容定向集,引入相对相容定向完备集的概念。
定义3.6:设P为偏序集,
,
,P称为相对相容定向完备集,若对于P中任意相对T的相容定向集D,最小上界
存在。
注3.7:相容定向完备集必为相对相容定向完备集,但相对相容定向完备集未必是相容定向完备集。
例3.8:如图2所示。
设
,
,规定P2中的偏序关系:若
,则
当且仅当
;若
,则按M普通的偏序关系;若
, ,则
。
,则
。
取
,则P2为相对T的相容定向完备集,但此时的P2不为相容定向完备集。
命题3.9:设P为偏序集,
,且
,若
,则P为相对相容定向完备集当且仅当P为相容定向完备集。

Figure 1. Hasse diagram of poset P1
图1. 偏序集P1的Hasse图

Figure 2. Hasse diagram of poset P2
图2. 偏序集P2的Hasse图
4. 相对相容连续偏序集
有了相对相容定向集和相对相容定向完备集概念后,下面自然的可以在相容定向完备偏序集上引入相对相容way below关系的概念。
定义4.1:设P为相对相容定向完备偏序集,其中
,且
,定义P上相对T的way below
关系如下:
,若任意
,
时,存在
,使得
,则称x相对于T相容小于y,记为
。如果
,则称x为P上相对于T的相容紧元。用
表示所有P中相对于T相容紧元,同时,可以记
,
。
命题4.2:设P为相对相容定向完备偏序集,其中
,且
,若对于任意 ,则下列结论成立:
,则下列结论成立:
1)
;
2)
;
3)
,
,若
存在,则
;
4) 若0存在且
,则
,有 ;
;
5)
。
证明:1)
,因P为相对相容定向完备集,故
存在,又
,若
,则存在
使得
,取
,易证
,进而有
。
2)
,因P为相对相容定向完备集,故
存在。若
,有
,又
,存在
使得
,进而
,所以
。
3)
,则
存在且 ,若
,因为
,
,故存在
使得
且
,进而
,所以
。
,若
,因为
,
,故存在
使得
且
,进而
,所以
。
4)
,若
,则存在
,使得
。又0为P上的最小元,即
,所以
。
5) 任意取
,则有
且
。进而
,而
,所以
。
下面利用相对相容way below关系,引入相对相容连续偏序集的概念。
定义4.3:设P为相对相容定向完备偏序集,其中
,且
,则称P为相对T的相容连续偏序集,若P满足下列两个条件:
1)
,
,
2)
为相对T的相容定向集。
定理4.4:设P为相容连续偏序集,
,
,则
有
。
证明:
,则
,因P为相容连续偏序集,故P为相容定向完备集。从而P为相对相容定向完备集,
,则D为相容定向集,故
存在且
。若
,则存在
使得
,从而有 ,进而
,即
,结论成立。
,进而
,即
,结论成立。
定理4.5:设P为相容连续偏序集,
,且
,则P为相对相容连续偏序集。
证明:首先,易证P为相对相容定向完备集。再者,
,由命题4.2知 为相对相容定向集。下证
成立。
,有
,从而
,可见y为集合
的一个上界,故
。再由定理4.4知
,所以
,即
。综合上述,P为相对相容连续偏序集。
为相对相容定向集。下证
成立。
,有
,从而
,可见y为集合
的一个上界,故
。再由定理4.4知
,所以
,即
。综合上述,P为相对相容连续偏序集。
注4.6:相对相容连续偏序集未必为相容连续偏序集。
例4.7:如图2所示,若令
,则P相对T的连续偏序集。然而,对于相容定向集M,
,P不为相容定向完备集,从而P不为相容连续偏序集。
定理4.8:设P为相容完备偏序集,其中
,且
,若
则P为相对相容连续偏序集当且仅当P相容连续偏序集。
下面定理说明相对相容连续偏序集是具有相应的插值性质的。
定理4.9:设P为相对相容连续偏序集,
,
,
,若
,则存在
,使得
。
证明:记
,因
且P为相对相容连续偏序集,易知必存在
,使得
,故
,可见
。下证集合S是相对相容定向集,
,则存在
,使得
且
。从而
,因P为相容完备偏序集,故
为相对相容定向集。从而 为定向集,进而存在
,使得
且
,由命题4.2得
且
。从而
,又因为
为定向集,故存在
使得
,
,又
。事实上,因
且
,即
,从而S为定向集。又
且
,所以S为相对相容定向集。因为
,事实上,因为P为相对相容连续偏序集,故
,从而
。又
,所以存在
使得
,进而存在
使得
,所以
,结论成立。
为定向集,进而存在
,使得
且
,由命题4.2得
且
。从而
,又因为
为定向集,故存在
使得
,
,又
。事实上,因
且
,即
,从而S为定向集。又
且
,所以S为相对相容定向集。因为
,事实上,因为P为相对相容连续偏序集,故
,从而
。又
,所以存在
使得
,进而存在
使得
,所以
,结论成立。
基金项目
国家自然科学基金资助项目(11361028),安徽高等学校省级自然科学研究重点项目(KJ2017A378),淮北师范大学研究生创新基金项目(2017yjscx07),淮北师范大学研究生教育教学研究项目(2017jyxm03)。