弧微分等价代换定理的适用范围

The Scope of Arc Differential Equivalent Substitution Theorem

摘要: 把平面光滑曲线弧微分拓展到空间坐标系中，完成二维条件下的弧微分与空间坐标下弧微分的等价代换，确定了弧微分等价代换定理的适用范围。弧微分等价代换定理可以有效解决有圆形场源存在的电磁场解析解算法问题，可作为高等院校数学和物理电磁学课程教材及教学的补充内容。

Abstract: The arc differential of planar smooth curve is extended to the three-dimensional coordinate system. According to the equivalent substitution relation between arc differential in two-dimensional condition and arc differential in three-dimensional coordinate system, the applicable scope of arc differential equivalent substitution theorem is determined. The equivalent substitution theorem of arc differential can effectively solve the algorithm of electromagnetic field analytical solutions with circular field sources, Can be used as a supplementary content of teaching materials and teaching for mathematics and physics electromagnetism courses in colleges and universities.

1. 引言

本文以讨论弧微分等价代换定理的适用范围，正确掌握其使用方法不错用为目的。求函数积分的解析解比近似数值解算法更有优越性，法国数学家刘维尔(Joseph Liouville，1809年3月24日生于法国加来海峡省圣奥梅尔，1882年9月8日卒于巴黎)1833年证明，应用广泛的全椭圆积分没有解析解 [1] ，尽管全椭圆积分形式很简单，鉴于此没有解析解的证明，180多年以来，只有采用近似数值解算法。只是近10多年，如“轴对称线圈磁场的精确计算方法研究” [2] 、“圆柱导体磁场的解析解算法研究” [3] 、“关于电磁场解析方法的一些认识” [4] 等论文相继发表，电磁场解析方法取得了巨大进步。使用弧微分等价代换定理，把平面光滑曲线的弧微分拓展到空间坐标系中，根据二维条件下的弧微分与空间坐标下的弧微分所构成优化的等价代换关系，通过积分变换，有效减少了积分变量的数量，积分过程避开了解全椭圆积分问题，变无理函数的积分为有理函数的积分，降低了积分的难度，积分结果得到了有限形式的封闭解，准确揭示了轴对称线圈、圆柱导体等空间磁场解析解算法的特征 [2] [3] [4] 。

尽管有关论文 [2] [3] 已对弧微分等价代换方法进行了探讨和表述，但对其一般性论证及适用范围问题仍缺乏进一步的明确。任何定理都有其适用范围，弧微分等价代换定理也不例外，其一般性论证以及确定其适用范围，对全面掌握和正确运用该定理的使用方法，防止错用是十分必要的，在遇到类似的计算问题时，发挥其精确解析解具有近似数值解算法所不能替代的优势 [3] ，可使有关的计算问题变得简单化，可提高计算的精确度和速度，编入大学数学和物理教材的话，对相关学科教学及工程领域的推广应用都显得很有必要。

2. 弧微分等价代换定理的一般性论证

2.1. 平面光滑曲线弧微分在平面及空间坐标下的表述

如图1所示，在平面坐标xoy内，光滑曲线C是y = f(x)在x = a到x = b之间的图象，在曲线C上取点A作为度量弧长的起点，并规定依x增大的方向作为弧的正向，C上已知点P(x,y)及邻点 $Q\left(x+\Delta x,y+\Delta y\right)$ ，s表示曲线弧 $\stackrel{⌢}{AP}$ 的长度，即

$s=\stackrel{⌢}{AP}$

显然，弧长s是随着x的确定而确定，因此弧长s是x的函数，记作

$s=s(x)$

连OP、OQ、PQ(=Δs)；其极坐标： $\angle POx=\Phi$ ， $\angle POQ=\Delta \Phi$ ， $\left|OP\right|=\rho$ ， $\left|OQ\right|=\rho +\Delta \rho$ ， $x=\rho \cos \Phi$ ，

Figure 1. Arc differential equivalent substitution

图1. 弧微分等价代换

$x+\Delta x=\left(\rho +\Delta \rho \right)\cos \left(\Phi +\Delta \Phi \right)$ ， $y=\rho \sin \Phi$ ， $y+\Delta y=\left(\rho +\Delta \rho \right)\sin \left(\Phi +\Delta \Phi \right)$ [5] ，过P作 $P{D}^{\prime }\perp OQ\cap D^{\prime }$ ；在立体坐标系中有任一关系点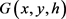，G在xoy平面内的投影为G'， $\left|G{G}^{\prime }\right|=h$ ，连GP、GQ，过P作 $PD\perp GQ\cap D$ ， $\left|GP\right|=\mathcal{l}$ ， $\left|GQ\right|=\mathcal{l}+\Delta \mathcal{l}$ ， $\angle G^{\prime }GP=\theta$ ， $\angle PGQ=\Delta \theta$ ， $\mathcal{l}=\mathcal{l}\left(\theta \right)$ [5] 。

讨论弧微分等价代换定理，即 $\text{d}s\left(\theta \right)=\text{d}s\left(\varphi \right)$ 成立。

1)：直角坐标xoy中(注意弦 $\left|PQ\right|$ 和Δx、Δy组成的小直角三角形)，

$\because \Delta s=\left|PQ\right|=\sqrt{{\left(x+\Delta x-x\right)}^2+{\left(y+\Delta y-y\right)}^2}=\sqrt{{\left(\Delta x\right)}^2+{\left(\Delta y\right)}^2}$ [6] [7] ，

$\therefore ds=\left(\underset{\Delta x\to 0}{\lim }\frac{\left|PQ\right|}{\Delta x}\right)dx=\left[\underset{\Delta y\to 0}{\lim }\frac{\sqrt{{\left(\Delta x\right)}^2+{\left(\Delta y\right)}^2}}{\Delta x}\right]dx=\sqrt{{\left(dx\right)}^2+{\left(dy\right)}^2}=\sqrt{1+{\left[f^{\prime }\left(x\right)\right]}^2}dx$ (1)

2)：极坐标下，对 $x=\rho \left(\varphi \right)\cos \varphi$ 求微分，得

$\text{d}x={\rho }^{\prime }\left(\varphi \right)\cos \varphi \text{d}\varphi -\rho \left(\varphi \right)\sin \varphi \text{d}\varphi ,$

对 $y=\rho \left(\varphi \right)\sin \varphi$ 求微分，得

$\text{d}y={\rho }^{\prime }\left(\varphi \right)\sin \varphi \text{d}\varphi +\rho \left(\varphi \right)\cos \varphi \text{d}\varphi ,$

$\begin{array}{l}\therefore ds=\sqrt{{\left(dx\right)}^2+{\left(dy\right)}^2}\\ =\sqrt{{\left[{\rho }^{\prime }\left(\varphi \right)\cos \varphi d\varphi -\rho \left(\varphi \right)\sin \varphi d\varphi \right]}^2+{\left[{\rho }^{\prime }\left(\varphi \right)\sin \varphi d\varphi +\rho \left(\varphi \right)\cos \varphi d\varphi \right]}^2}\\ =\sqrt{{\left[{\rho }^{\prime }\left(\varphi \right)\right]}^2+{\rho }^2\left(\varphi \right)}d\varphi \end{array}$ (2)

结果：式(1) = 式(2)。

3) 求弧微分ds(Φ) (参考图1)

① 求微小弦的改变量：

在微小RtΔPD'Q中，

$\because \left|P{D}^{\prime }\right|=\rho \sin \Delta \varphi ,\left|Q{D}^{\prime }\right|=\left|OQ\right|-\left|O{D}^{\prime }\right|=\rho +\Delta \rho -\rho \cos \Delta \varphi =\Delta \rho +\rho \left(1-\cos \Delta \varphi \right),$

$\therefore \left|PQ\right|=\Delta s=\sqrt{{\left|Q{D}^{\prime }\right|}^2+{\left|P{D}^{\prime }\right|}^2}=\sqrt{{\left[\Delta \rho +\rho \left(1-\cos \Delta \varphi \right)\right]}^2+{\left(\rho \sin \Delta \varphi \right)}^2}$ [5] 。

② $\begin{array}{c}ds\left(\varphi \right)=\left(\underset{\Delta \varphi \to 0}{\lim }\frac{\Delta s}{\Delta \varphi }\right)d\varphi =\left[\underset{\Delta \varphi \to 0}{\lim }\frac{\sqrt{{\left[\Delta \rho +\rho \left(1-\cos \Delta \varphi \right)\right]}^2+{\left(\rho \sin \Delta \varphi \right)}^2}}{\Delta \varphi }\right]d\varphi \\ =\sqrt{\frac{{\left[d\rho \left(\varphi \right)\right]}^2}{{\left(d\varphi \right)}^2}+{\rho }^2\left(\varphi \right)}d\varphi =\sqrt{{\left[{\rho }^{\prime }\left(\varphi \right)\right]}^2+{\rho }^2\left(\varphi \right)}d\varphi \end{array}$ (3)

结果：式(3) = 式(2)。

4) 求弧微分ds(θ)(参考图1)

① 求微小弦的改变量：

在空间坐标系中，注意小RtΔPDQ，

$\because \left|PD\right|=\mathcal{l}\sin \Delta \theta ,\left|QD\right|=\left|GQ\right|-\left|GD\right|=\mathcal{l}+\Delta \mathcal{l}-\mathcal{l}\cos \Delta \theta =\Delta \mathcal{l}+\mathcal{l}\left(1-\cos \Delta \theta \right),$

$\therefore \left|PQ\right|=\Delta s\left(\theta \right)=\sqrt{{\left|QD\right|}^2+{\left|PD\right|}^2}=\sqrt{{\left[\Delta \mathcal{l}+\mathcal{l}\left(1-\cos \Delta \theta \right)\right]}^2+{\left(\mathcal{l}\sin \Delta \theta \right)}^2}$ [5] 。

② $\begin{array}{c}ds\left(\theta \right)=\left[\underset{\Delta \theta \to 0}{\lim }\frac{\Delta s\left(\theta \right)}{\Delta \theta }\right]d\theta =\left[\underset{\Delta \theta \to 0}{\lim }\frac{\sqrt{{\left[\Delta \mathcal{l}+\mathcal{l}\left(1-\cos \Delta \theta \right)\right]}^2+{\left(\mathcal{l}\sin \Delta \theta \right)}^2}}{\Delta \theta }\right]d\theta \\ =\sqrt{\frac{{\left[d\mathcal{l}\left(\theta \right)\right]}^2}{{\left(d\theta \right)}^2}+{\mathcal{l}}^2\left(\theta \right)}d\theta =\sqrt{{\left[{\mathcal{l}}^{\prime }\left(\theta \right)\right]}^2+{\mathcal{l}}^2\left(\theta \right)}d\theta \end{array}$ (4)

2.2. 弧微分等价代换定理，即证明 $ds\left(\theta \right)=\text{d}s\left(\varphi \right)$ 成立

如图1，在ΔPD'Q中,

$\left|PQ\right|=\Delta s\left(\varphi \right)=\sqrt{{\left|Q{D}^{\prime }\right|}^2+{\left|P{D}^{\prime }\right|}^2}=\sqrt{{\left[\Delta \rho +\rho \left(1-\cos \Delta \varphi \right)\right]}^2+{\left(\rho \sin \Delta \varphi \right)}^2},$

在ΔPDQ中,

$\left|PQ\right|=\Delta s\left(\theta \right)=\sqrt{{\left|QD\right|}^2+{\left|PD\right|}^2}=\sqrt{{\left[\Delta \mathcal{l}+\mathcal{l}\left(1-\cos \Delta \theta \right)\right]}^2+{\left(\mathcal{l}\sin \Delta \theta \right)}^2},$

因 $\left|PQ\right|$ ( = Δs)是小RtΔPD'Q和小RtΔPDQ公共斜边，所以

$\Delta s\left(\theta \right)=\Delta s\left(\Phi \right)\left[=\left|PQ\right|\right].$

令函数

$Z=\Delta s\left(\varphi \right)-\Delta s\left(\theta \right)=\sqrt{{\left[\Delta \rho +\rho \left(1-\cos \Delta \varphi \right)\right]}^2+{\left(\rho \sin \Delta \varphi \right)}^2}-\sqrt{{\left[\Delta \mathcal{l}+\mathcal{l}\left(1-\cos \Delta \theta \right)\right]}^2+{\left(\mathcal{l}\sin \Delta \theta \right)}^2}=0$

函数Z对Δs(Φ)和Δs(θ)的偏导数：

$\frac{\partial Z}{\partial \Delta s\left(\varphi \right)}=\underset{\Delta \varphi \to 0}{\lim }\frac{\Delta s}{\Delta \varphi }=\underset{\Delta \varphi \to 0}{\lim }\frac{\sqrt{{\left[\Delta \rho +\rho \left(1-\cos \Delta \varphi \right)\right]}^2+{\left(\rho \sin \Delta \varphi \right)}^2}}{\Delta \varphi }=\sqrt{{\left(\frac{d\rho }{d\varphi }\right)}^2+{\rho }^2}$ [8] [9] ，

$\frac{\partial Z}{\partial \Delta s\left(\theta \right)}=\underset{\Delta \theta \to 0}{\lim }\frac{\Delta s}{\Delta \theta }=\underset{\Delta \theta \to 0}{\lim }\frac{\sqrt{{\left[\Delta \mathcal{l}+\mathcal{l}\left(1-\cos \Delta \theta \right)\right]}^2+{\left(\mathcal{l}\sin \Delta \theta \right)}^2}}{\Delta \theta }=\sqrt{{\left(\frac{d\mathcal{l}}{d\theta }\right)}^2+{\mathcal{l}}^2}$ [8] [9] 。

函数Z的全微分：因为 $Z=\Delta s\left(\Phi \right)-\Delta s\left(\theta \right)=0$ ，

且 ${dZ|}_{\left[\Delta s\left(\varphi \right),\Delta s\left(\theta \right)\right]}=\frac{\partial Z}{\partial \Delta s\left(\varphi \right)}d\varphi -\frac{\partial Z}{\partial \Delta s\left(\theta \right)}d\theta =\sqrt{{\left(\frac{d\rho }{d\varphi }\right)}^2+{\rho }^2}d\varphi -\sqrt{{\left(\frac{d\mathcal{l}}{d\theta }\right)}^2+{\mathcal{l}}^2}d\theta =0$ ，

即 $\sqrt{{\left(\frac{d\rho }{d\varphi }\right)}^2+{\rho }^2}d\varphi =\sqrt{{\left(\frac{d\mathcal{l}}{d\theta }\right)}^2+{\mathcal{l}}^2}d\theta$ ，

所以 $\text{d}s\left(\Phi \right)=\text{d}s\left(\theta \right)$ [即式(4)=式(3)]成立。

说明：在空间坐标系中，因 $\left|G{G}^{\prime }\right|=h$ 是函数y = f(x)的曲线C所在平面的已知垂线，沿曲线C，当Q→P(或 $\stackrel{⌢}{PQ}\to 0$ )时，直角ΔGG'Q→直角ΔGG'P(全等)，即ΔGG'Q和ΔGG'P各自所在的平面趋向于同一极限，有GQ→GP(且 $GP\subset \Delta G{G}^{\prime }P$ 所在平面)、 $\theta +\Delta \theta \to \angle QG{G}^{\prime }$ 。

且ΔGG'P中，ℓ = h/cosθ，则

$ds\left(\theta \right)=\sqrt{{\left(\frac{d\mathcal{l}}{d\theta }\right)}^2+{\mathcal{l}}^2}d\theta =\sqrt{\frac{{\left(\text{d}\frac{h}{\cos \theta }\right)}^2}{{\left(\text{d}\theta \right)}^2}+{\left(\frac{h}{\cos \theta }\right)}^2}\text{d}\theta =\frac{h}{{\cos }^2\theta }\text{d}\theta$ [2] 。

3. 弧微分等价代换定理适用范围的讨论

条件(1)：使

$ds\left(\theta \right)=\sqrt{{\left(\frac{d\mathcal{l}}{d\theta }\right)}^2+{\mathcal{l}}^2}d\theta =\sqrt{\frac{{\left(\text{d}\frac{h}{\cos \theta }\right)}^2}{{\left(\text{d}\theta \right)}^2}+{\left(\frac{h}{\cos \theta }\right)}^2}\text{d}\theta =\frac{h}{{\cos }^2\theta }\text{d}\theta =\text{d}s\left(\varphi \right).$

成立，必须满足h ≠ 0，即G点不在xoy平面内。

证明(反证法)：

假设h = 0时，

$ds\left(\theta \right)=\sqrt{{\left(\frac{d\mathcal{l}}{d\theta }\right)}^2+{\mathcal{l}}^2}d\theta =\sqrt{\frac{{\left(\text{d}\frac{h}{\cos \theta }\right)}^2}{{\left(\text{d}\theta \right)}^2}+{\left(\frac{h}{\cos \theta }\right)}^2}\text{d}\theta =\frac{h}{{\cos }^2\theta }\text{d}\theta =\text{d}s(\varphi )$

成立。有

$ds\left(\theta \right)=\sqrt{{\left(\frac{d\mathcal{l}}{d\theta }\right)}^2+{\mathcal{l}}^2}d\theta =\sqrt{\frac{{\left(\text{d}\frac{h}{\cos \theta }\right)}^2}{{\left(\text{d}\theta \right)}^2}+{\left(\frac{h}{\cos \theta }\right)}^2}\text{d}\theta =\frac{h}{{\cos }^2\theta }\text{d}\theta =0,$

即

$ds\left(\theta \right)=0,$

为常量，且

$\text{d}s\left(\varphi \right)\ne 0,$

有

$ds\left(\theta \right)\ne \text{d}s\left(\varphi \right),$

当h = 0时，则

$ds\left(\theta \right)=\text{d}s\left(\varphi \right),$

不成立。

其几何意义，对于当G点落入xoy平面内时，弧微分等价代换定理不再适用。

条件(2)：使

$ds\left(\theta \right)=\sqrt{{\left(\frac{d\mathcal{l}}{d\theta }\right)}^2+{\mathcal{l}}^2}d\theta =\sqrt{\frac{{\left(\text{d}\frac{h}{\cos \theta }\right)}^2}{{\left(\text{d}\theta \right)}^2}+{\left(\frac{h}{\cos \theta }\right)}^2}\text{d}\theta =\frac{h}{{\cos }^2\theta }d\theta ,$

成立，必须符合θ不为常量。

证明(反证法)：

假设θ为常量时，

$ds\left(\theta \right)=\sqrt{{\left(\frac{d\mathcal{l}}{d\theta }\right)}^2+{\mathcal{l}}^2}d\theta =\sqrt{\frac{{\left(\text{d}\frac{h}{\cos \theta }\right)}^2}{{\left(\text{d}\theta \right)}^2}+{\left(\frac{h}{\cos \theta }\right)}^2}\text{d}\theta =\frac{h}{{\cos }^2\theta }\text{d}\theta =\text{d}s\left(\varphi \right),$

成立。有

$ds\left(\theta \right)=\sqrt{{\left(\frac{d\mathcal{l}}{d\theta }\right)}^2+{\mathcal{l}}^2}d\theta =\sqrt{\frac{{\left(\text{d}\frac{h}{\cos \theta }\right)}^2}{{\left(\text{d}\theta \right)}^2}+{\left(\frac{h}{\cos \theta }\right)}^2}d\theta =\frac{h}{{\cos }^2\theta }\text{d}\theta =0,$

即

$ds\left(\theta \right)=0,$

为常量，且

$\text{d}s\left(\varphi \right)\ne 0,$

有

$ds\left(\theta \right)\ne \text{d}s\left(\varphi \right),$

当θ为常量时，则

$ds\left(\theta \right)=\text{d}s\left(\varphi \right),$

不成立。

例如圆环线圈、圆柱导体磁场的计算，对于其圆环的圆心轴线、圆柱导体中心轴线上的磁场计算时，由于θ为常量，则弧微分等价代换定理在此不再适用。但对于曲线所在的坐标面和中心轴线之外空间的任一点，弧微分等价代换定理均适用，特别对二维、三维场源的磁场力及功的计算时，往往能规避以上不适用条件的限制，这可在实际计算中去体验。

4. 弧微分等价代换定理的完整表述

通过以上对 $\text{d}s\left(\Phi \right)=\text{d}s\left(\theta \right)$ 即弧微分等价代换定理及其适用范围的证明和分析,可以得出弧微分等价代换定理的完整表述：

直角坐标系中，平面光滑曲线C是函数y = f(x)在区间(a,b)内的图像，其弧微分

$\text{d}s=\sqrt{1+{\left[f^{\prime }\left(x\right)\right]}^2}\text{d}x$ [10] ；

极坐标中平面光滑曲线C满足ρ = ρ(Ф)，[Ф₀ ≤ Ф ≤ Ф_n] [也即ρ(Ф)在(Ф₀, Ф_n)上有连续导数]，其弧微分

$\text{d}s\left(\varphi \right)=\sqrt{{\left[\rho \left(\varphi \right)\right]}^2+{\left[{\rho }^{\prime }\left(\varphi \right)\right]}^2}\text{d}\varphi$ [10] ；

在所构成的空间坐标系中，存在任一已知关系点 $P\left(x,y,h\right)$ ，P点到平面光滑曲线C弧微分ds(Φ)的距离为ℓ = ℓ(θ)，θ为P点直线z = h(且h ≠ 0)与直线ℓ = ℓ(θ) (且θ不为常量)的夹角，则弧微分存在

$\text{d}s\left(\Phi \right)=\text{d}s\left(\theta \right),$

即

$\sqrt{{\left[\rho \left(\varphi \right)\right]}^2+{\left[{\rho }^{\prime }\left(\varphi \right)\right]}^2}\text{d}\varphi =\sqrt{{\left[\mathcal{l}\left(\theta \right)\right]}^2+{\left[{\mathcal{l}}^{\prime }\left(\theta \right)\right]}^2}\text{d}\theta \left[或=\frac{h}{{\cos }^2\theta }\text{d}\theta \right]$ [2]

同样

$\sqrt{1+{\left[f^{\prime }\left(x\right)\right]}^2}\text{d}x=\sqrt{{\left[\mathcal{l}\left(\theta \right)\right]}^2+{\left[{\mathcal{l}}^{\prime }\left(\theta \right)\right]}^2}\text{d}\theta \left[或=\frac{h}{{\cos }^2\theta }\text{d}\theta \right]$ [2]

称之为平面光滑曲线弧微分与空间坐标系中弧微分的等价代换定理，简称弧微分等价代换定理 [3] 。

根据弧微分等价代换定理，如图1，可针对具体问题的需要，把曲线C在xoy中的平面扇形OPQ的弧微分ds(Φ)变换成由空间扇形GPQ构成的弧微分形式ds(θ)。由于

$\text{d}s\left(\Phi \right)=\text{d}s(\theta )$

是等价代换，则弧微分等价代换定理的应用，在解决有关函数积分的解析解算法方面所具有的优势，是平面曲线弧微分所不能替代的 [2] [3] 。

5. 弧微分等价代换定理在圆盘线圈磁场解析解算法中的应用

5.1. 弧微分等价代换定理对圆环电流磁场解析解解算法的回顾

5.1.1. 圆环电流任一电流元在空间点轴向(dB_z)、径向(dB_r)、周向(dB_γ)磁场的微分.

圆盘线圈在电机、射频识别、电磁炉等技术中应用广泛，结合该算法应用于求圆盘线圈磁场的解析解,以再次验证弧微分等价代换定理。如图2，半径为R的单一圆环电流⊙O上任一 $P\left(R\cos {\varphi }_0,R\sin {\varphi }_0,0\right)$ 点取得电流元I′ds，其空间任一待求磁场点 $G\left(r\cos \gamma ,r\sin \gamma ,h\right)$ 位于与⊙O同圆心轴、距离⊙O环面为h、半径为r的平行圆⊙O′周上，⊙O上P点切线AD交x、y轴于A、D， $\angle DPG=\alpha$ ， $\angle POA={\Phi }_0$ ， $\angle POG\prime =\Phi$ ， $\angle O\prime =\angle G\prime OA=\gamma$ ， $\left|GP\right|=\mathcal{l}$ ， $\left|G{G}^{\prime }\right|=h$ ， $\angle G\prime GP=\theta$ ，有cosθ = h/ℓ，使用弧微分等价代换定理，先讨论圆环电流空间G点处的径向 $\left(\text{d}{B}_r\right)$ 、轴向 $\left(\text{d}{B}_z\right)$ 、周向 $\left(\text{d}{B}_{\gamma }\right)$ 磁场的解析解算法，再求圆盘线圈磁场的解析解。

由比奥─萨伐尔定律： $\text{d}B=\frac{{\mu }_{\text{0}}}{\text{4π}}{I}^{\prime }\text{d}s\times \mathcal{l}$ ，即 $\text{d}B=\frac{{\mu }_{\text{0}}{I}^{\prime }}{\text{4π}}\frac{\text{sin}\alpha }{{\mathcal{l}}^{\text{2}}}\text{d}s$ ，其中ds = RdΦ，ℓ = h/cosθ， $\sin \alpha =\sqrt{\frac{h^2+{\left(r\cos \varphi -R\right)}^2}{h^2+R^2+r^2-2Rr\cos \varphi }}$ 。有

$dB=\frac{{\mu }_0{I}^{\prime }}{\text{4π}}\frac{\sin \alpha }{{\mathcal{l}}^2}ds=\frac{{\mu }_0{I}^{\prime }}{\text{4π}}\frac{\sqrt{h^2+{\left(r\cos \varphi -R\right)}^2}}{{\left[h^2+R^2+r^2-2Rr\cos \varphi \right]}^{3/2}}ds\left(\varphi \right)$ ，dB方向：I′ds × ℓ。

在平行⊙O'周P点有(矢量和)： $\text{d}B=\text{d}{B}_z\left(轴向\right)+\text{d}{B}_r\left(径向\right)+\text{d}{B}_{\gamma }\left(周向\right)$ ，且

$\text{d}{B}_z=\frac{{\mu }_0{I}^{\prime }}{\text{4π}}\frac{\sqrt{h^2+{\left(r\cos \varphi -R\right)}^2}}{{\left[h^2+R^2+r^2-2Rr\cos \varphi \right]}^{3/2}}\cos \left(\text{d}B,\text{d}{B}_z\right)ds\left(\varphi \right)=\frac{{\mu }_0{I}^{\prime }}{\text{4π}}\frac{r\cos \varphi -R}{{\left[h^2+R^2+r^2-2Rr\cos \varphi \right]}^{3/2}}ds(\varphi )$

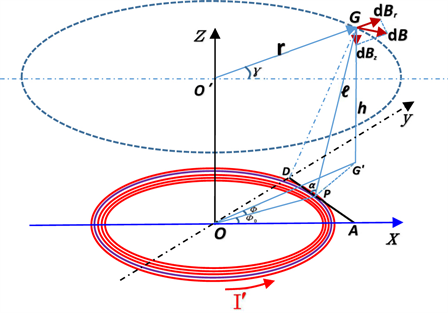
Figure 2. Magnetic field of the disk coil

图2. 圆盘线圈的磁场

$\text{d}{B}_r=\frac{{\mu }_0{I}^{\prime }}{\text{4π}}\frac{\sqrt{h^2+{\left(r\cos \varphi -R\right)}^2}}{{\left[h^2+R^2+r^2-2Rr\cos \varphi \right]}^{3/2}}\cos \left(\text{d}B,\text{d}{B}_r\right)ds(\varphi )=\frac{{\mu }_0{I}^{\prime }h}{\text{4π}}\frac{\cos \varphi }{{\left[h^2+R^2+r^2-2Rr\cos \varphi \right]}^{3/2}}ds(\varphi )$

$\text{d}{B}_{\gamma }=\frac{{\mu }_0{I}^{\prime }}{\text{4π}}\frac{\sqrt{h^2+{\left(r\cos \varphi -R\right)}^2}}{{\left[h^2+R^2+r^2-2Rr\cos \varphi \right]}^{3/2}}\cos \left(\text{d}B,\text{d}{B}_{\gamma }\right)ds\left(\varphi \right)=\frac{{\mu }_0{I}^{\prime }}{\text{4π}}\frac{-h\sin \varphi }{{\left[h^2+R^2+r^2-2Rr\cos \varphi \right]}^{3/2}}ds(\varphi )$

5.1.2. 圆环电流在空间点的轴向(B_z)、径向(B_x)、周向(B_γ)磁场的解析式

任一待球磁场点G、RtΔGG′P、圆环电流及其电流元I′ds之间满足弧微分等价代换定理的条件，即

$\text{d}s=R\text{d}\varphi =\frac{h}{{\cos }^2\theta }\text{d}\theta ,$

并

${\mathcal{l}}^2=h^2+R^2+r^2-2Rr\cos \Phi =h^2/{\cos }^2\theta ,$

分别求得：

$\begin{array}{c}{B}_z={\displaystyle \oint \frac{{\mu }_0{I}^{\prime }}{\text{4π}}\frac{r\cos \varphi -R}{{\left[h^2+R^2+r^2-2Rr\cos \varphi \right]}^{3/2}}ds\left(\varphi \right)}\\ =\frac{{\mu }_0{I}^{\prime }}{\text{4π}}2{\displaystyle {\int }_{{\theta }_1=\arcsin \frac{R-r}{\sqrt{h^2+{\left(R-r\right)}^2}}}^{{\theta }_2=\arcsin \frac{R+r}{\sqrt{h^2+{\left(R+r\right)}^2}}}\frac{\frac{r}{2Rr}\left[h^2+R^2+r^2-{\left(\frac{h}{\cos \theta }\right)}^2\right]-R}{{\left(\frac{h}{\cos \theta }\right)}^3}}\frac{h}{{\cos }^2\theta }d\theta \\ =\frac{{\mu }_0{I}^{\prime }}{4\text{π}R{h}^2}\{\left(h^2+r^2-R^2\right)\left[\frac{R+r}{\sqrt{h^2+{\left(R+r\right)}^2}}-\frac{R-r}{\sqrt{h^2+{\left(R-r\right)}^2}}\right]\\ -h^2\ln \left|\frac{\sqrt{h^2+{\left(R+r\right)}^2}+\left(R+r\right)}{\sqrt{h^2+{\left(R-r\right)}^2}+\left(R-r\right)}\right|\}\end{array}$ [2]

$\begin{array}{c}{B}_r=\frac{{\mu }_0{I}^{\prime }h}{4\text{π}}{\displaystyle \oint \frac{\cos \varphi }{{\left[h^2+R^2+r^2-2Rr\cos \varphi \right]}^{3/2}}d\left(R\varphi \right)}\\ =\frac{{\mu }_0{I}^{\prime }}{4\text{π}2Rrh}2{\displaystyle {\int }_{{\theta }_1=\arcsin \frac{R-r}{\sqrt{h^2+{\left(R-r\right)}^2}}}^{{\theta }_2=\arcsin \frac{R+r}{\sqrt{h^2+{\left(R+r\right)}^2}}}\left[\left(h^2+R^2+r^2\right)\cos \theta -h^2\frac{1}{\cos \theta }\right]\text{d}\theta }\\ =\frac{{\mu }_0{I}^{\prime }}{4\text{π}Rrh}\{\left(h^2+R^2+r^2\right)\left[\frac{R+r}{\sqrt{h^2+{\left(R+r\right)}^2}}-\frac{R-r}{\sqrt{h^2+{\left(R-r\right)}^2}}\right]\\ -h^2\ln \left|\frac{\sqrt{h^2+{\left(R+r\right)}^2}+\left(R+r\right)}{\sqrt{h^2+{\left(R-r\right)}^2}+\left(R-r\right)}\right|\}\end{array}$ [2]

$B_{\gamma }={\displaystyle {\int }_{-\text{π}}^{\text{π}}\frac{{\mu }_0{I}^{\prime }R}{\text{4π}}\frac{-h\sin \varphi }{{\left[h^2+R^2+r^2-2Rr\cos \varphi \right]}^{3/2}}d\varphi }=0$ [2] .

5.2. 弧微分等价代换定理对圆盘线圈磁场的解析算法

如图2所示，使用微元法，对内、外半径为R₁、R₂的圆盘线圈在任一待求磁场点G处的磁场，采用半径分别为R₁、R₂的2个实芯圆盘线圈在G点产生磁场的差值算法的路子；R₁→R₂上单位厚度电流环数为m(=M/R_x)，R_x是实芯圆盘线圈的半径，M是该实芯圆盘线圈总的电流匝数，在R_x处选取线圈元素dR_x，dR_x电流环个数为 $mI\prime \text{d}{R}_x=MI\prime \text{d}{R}_x/R_x=I_{Rx}\text{d}{R}_x/R_x$ ，I_Rx (=MI′)是通过实芯圆盘线圈的总电流强度。探讨该圆盘线圈外与其同圆心轴的平行圆⊙O′周上任一待求磁场点G的轴向B_z、径向B_r、周向B_γ磁场算法。[I是R₁→R₂上的面电流；有 $I_{\text{1}}=R_{\text{1}}I/\left(R_{\text{2}}-R_{\text{1}}\right)$ ； $I_{\text{2}}=R_{\text{2}}I/\left(R_{\text{2}}-R_{\text{1}}\right)$ ]。

5.2.1. 圆盘线圈轴向磁场的解析解

$\begin{array}{c}{B}_{z\left(R_x\right)}=\frac{{\mu }_0{I}_{R_x}}{4\text{π}{h}^2}{\displaystyle {\int }_{R_1}^{R_2}\frac{1}{R_x^2}}\{\left(h^2+r^2-R_x^2\right)\left[\frac{R_x+r}{\sqrt{h^2+{\left(R_x+r\right)}^2}}-\frac{R_x-r}{\sqrt{h^2+{\left(R_x-r\right)}^2}}\right]\\ -h^2\ln \left|\frac{\sqrt{h^2+{\left(R_x+r\right)}^2}+\left(R_x+r\right)}{\sqrt{h^2+{\left(R_x-r\right)}^2}+\left(R_x-r\right)}\right|\}d{R}_x\\ =\frac{{\mu }_0}{4\text{π}{h}^2}{R}_2\frac{I}{R_2-R_1}\{-\frac{R_2+r}{R_2}\sqrt{h^2+{\left(R_2+r\right)}^2}\underset{}{\overset{\begin{array}{l}\\ \end{array}}{}}\\ +\frac{R_2-r}{R_2}\sqrt{h^2+{\left(R_2-r\right)}^2}+\frac{h^2}{R_2}\ln \left|\frac{\sqrt{h^2+{\left(R_2+r\right)}^2}+R_2+r}{\sqrt{h^2+{\left(R_2-r\right)}^2}+R_2-r}\right|\}\\ -\frac{{\mu }_0}{4\text{π}{h}^2}{R}_1\frac{I}{R_2-R_1}\{-\frac{R_1+r}{R_1}\sqrt{h^2+{\left(R_1+r\right)}^2}\underset{}{\overset{\begin{array}{l}\\ \end{array}}{}}\end{array}$

$+\frac{R_1-r}{R_1}\sqrt{h^2+{\left(R_1-r\right)}^2}+\frac{h^2}{R_1}\ln \left|\frac{\sqrt{h^2+{\left(R_1+r\right)}^2}+R_1+r}{\sqrt{h^2+{\left(R_1-r\right)}^2}+R_1-r}\right|\}$ [10] [11]

$R_1=0.8,R_2=1.0,r=1.01$ ；(μ₀、π、I为常量)

$h\subset \left\{2,1.5,1.0,0.8,0.6,0.4,0.2,0.01,\ne 0,-0.01,-0.2,-0.4,-0.6,-0.8,-1.0,-1.5,-2\right\}.$

$\begin{array}{c}\left[4\text{π}/\left({\mu }_{0}I\right)\right]B_z{}_{\left(R_1\to R_2\right)}\subset \{-0.6558125,-1.326174,-5.508308,-9.985637,-22.920225,\\ -91.94955,-36013.28,-36013.28,-91.94955,-22.920225,\\ -9.985637,-5.508308,-1.326174,-0.6558125\}\end{array}$

5.2.2. 圆盘线圈径向磁场的解析解

$\begin{array}{c}{B}_r=\frac{{\mu }_{0}I}{4\text{π}rh}{\displaystyle {\int }_{R_1}^{R_2}\frac{1}{R_x^2}}\{\left(h^2+R_x^2+r^2\right)\left[\frac{R_x+r}{\sqrt{h^2+{\left(R_x+r\right)}^2}}-\frac{R_x-r}{\sqrt{h^2+{\left(R_x-r\right)}^2}}\right]\\ -h^2\ln \left|\frac{\sqrt{h^2+{\left(R_x+r\right)}^2}+\left(R_x+r\right)}{\sqrt{h^2+{\left(R_x-r\right)}^2}+\left(R_x-r\right)}\right|\}d{R}_x\\ =\frac{{\mu }_0}{4\text{π}rh}\left(R_2\frac{I}{R_2-R_1}\right)\{\frac{R_2-r}{R_2}\sqrt{h^2+{\left(R_2+r\right)}^2}\underset{}{\overset{\begin{array}{l}\\ \end{array}}{}}\\ -\frac{R_2+r}{R_2}\sqrt{h^2+{\left(R_2-r\right)}^2}+\frac{h^2}{R_2}\ln \left|\frac{\sqrt{h^2+{\left(R_2+r\right)}^2}+R_2+r}{\sqrt{h^2+{\left(R_2-r\right)}^2}+R_2-r}\right|\}\\ -\frac{{\mu }_0}{4\text{π}rh}\left(R_1\frac{I}{R_2-R_1}\right)\{\frac{R_1-r}{R_1}\sqrt{h^2+{\left(R_1+r\right)}^2}\underset{}{\overset{\begin{array}{l}\\ \end{array}}{}}\end{array}$

$-\frac{R_1+r}{R_1}\sqrt{h^2+{\left(R_1-r\right)}^2}+\frac{h^2}{R_1}\ln \left|\frac{\sqrt{h^2+{(R_1+r)}^2}+R_1+r}{\sqrt{h^2+{(R_1-r)}^2}+R_1-r}\right|\}$ [10] [11]

$R_1=0.8,R_2=1.0,r=1.01$ ，(μ₀、π、I为常量)；

$h\subset \left\{2.0,1.5,1.0,0.8,0.6,0.4,0.2,0.01,-0.01,-0.2,-0.4,-0.6,-0.8,-1.0,-1.5,-2.0\right\}.$

$\begin{array}{c}\left[4\text{π}/\left({\mu }_{0}I\right)\right]B_r{}_{\left(R_1\to R_2\right)}\subset \{0.113531,0.268483,0.72033,1.154638,1.999366,2.74873,\\ 11.240817,351.712277,-351.712277,-11.240817,-2.74873,\\ -1.999366,-1.154638,-0.72033,-0.268483,-0.113531\}\end{array}$

5.2.3. 圆盘线圈周向磁场的解析解

因为圆环电流的周向磁场：

$B_{\gamma }={\displaystyle {\int }_{-\text{π}}^{\text{π}}\frac{{\mu }_{0}IR}{4\text{π}}\frac{-h\sin \varphi }{{\left[h^2+R^2+r^2-2Rr\cos \varphi \right]}^{3/2}}d\varphi }=0$

所以圆盘线圈电流的周向磁场

$B_{\gamma }{}_{\left(盘\right)}=0.$

6. 结论

把平面光滑曲线弧微分拓展到空间坐标系中，利用空间坐标下的弧微分对二维条件下弧微分所构成的优化等价代换关系，得到了弧微分等价代换定理，还进一步确定了其适用范围，完善了定理的内容。弧微分等价代换定理的应用可以有效解决有圆形场源存在的电磁场解析解算法等问题，可作为高等院校数学和物理电磁学课程教材及教学的补充内容。