1. 引言
数字图书馆以其信息容量大、传输速度快、时空限制少等优势,已成为读者阅读文献的主流平台。以中国知网CNKI为例,作为目前全球最大的中文数字图书馆,CNKI已拥有40多个国家及地区的众多读者,日均访问量超过100万人次。在集中文献资源的同时,如何向读者提供导向性强、个性化好的服务,是数字图书馆向智慧图书馆转变的关键。
文献阅读流是数字图书馆下读者产生的阅读事件组成的事件流,其中蕴藏着丰富的语义模式。文献智能推荐旨在对文献阅读流进行分析,挖掘频繁出现的文献序列(即频繁情节),从而发现读者的阅读习惯和预测读者的阅读倾向,这将有助于数字图书馆提高文献资源的利用率并向读者提供个性化的服务。
自Manilla [1] 等人引入事件流上的频繁情节挖掘问题以来,众多学者对此展开了研究,提出了许多代表性算法。WINEPI [1] 、WinMiner [2] 和HUEM-GAO [3] 算法都是基于一个情节出现在其中的滑动窗口的个数来统计该情节的支持度,而MINEPI [1] 、EPT [4] 、Clo_episode [5] 、Ap-epi [6] 、UP-Span [7] 、DMinEpi [8] 和MELLO [9] 等算法则是基于一个情节的最小发生(指这样的一个时间区间,所考虑的情节在其中发生,但不在其任何子区间上发生)次数来计算该情节的支持度。然而,这些算法在挖掘过程中需要多遍扫描事件流,并且产生了大量的候选情节。另外,这些算法在计算一个情节的支持度时都可能包含了该情节多次重叠的发生,从而会导致情节发生的“过计数”问题。例如,设事件流S = <(A,1), (A,2), (B,3), (D,4), (A,5), (C,6), (B,7), (E,8), (A,9), (C,10), (B,11), (A,12), (C,13)>,窗口大小为3,则事件流S被分为13 − 1 + 3 = 15个滑动窗口,即W1 = <(A,1)>,W2 = <(A,1), (A,2)>,W3 = <(A,1), (A,2), (B,3)>,W4 = <(A,2), (B,3), (D,4)>,W5 = <(B,3), (D,4), (A,5)>等,尽管情节
在S上只出现了一次,但由WINEPI等算法计算得到的情节
的支持度却为2(对应着两个重叠的滑动窗口W4和W5),由MINEPI等算法计算得到的情节
的支持度为3 (对应着三个重叠的最小区间[2,6], [5,10], [9,13])。
为了解决情节发生的“过计数”问题,学者们基于非重叠发生(一个情节的两次发生是非重叠的,当且仅当其中的一次发生出现在另一次发生之后)计数提出了事件流频繁情节挖掘算法Discovery Non Over [10] 、NONOVERLAPPING [11] 和NONEPI [12] ,这些算法为每个情节使用了一个自动机,通过单遍扫描事件序列来跟踪这些自动机的状态迁移,从而统计出相应情节在事件流上的发生次数。虽然这些算法较好地解决了情节发生的“过计数”问题,但由于非重叠发生未必是最小发生,所以这些算法挖掘的频繁情节并不能很好地描述一个情节中事件类型之间的紧随关系。例如,由算法NONEPI得到的情节
在事件流S上的第一次发生是[1,6] (即<(A,1), (B,3), (C,6)>),并不是最小发生[2,6] (即<(A,2), (B,3), (C,6)>)。
为此,本文提出了一种事件流频繁情节挖掘算法MANEPI (Minimal And Non-overlapping EPIsode)。该算法基于最小且非重叠发生来计算一个情节的支持度,既可以很好地描述一个情节中事件类型之间的紧随关系,又可以避免情节发生的“过计数”问题。该算法采用深度优先搜索策略来挖掘频繁情节,只需要单遍扫描事件流且不产生任何候选情节,大大提高挖掘效率。另外,该算法使用共享前缀树来存储频繁情节,并利用情节单调性压缩频繁情节的搜索空间,加速挖掘过程。理论分析和实验评估表明该算法能有效地挖掘给定事件流上的频繁情节。
2. 预备知识
2.1. 基本概念
定义1 (事件流):给定事件类型集
,一个事件就是一个二元组(E,t),其中,E Î ε,t表示该事件的发生时间。定义在ε上的事件流S是由若干事件按发生时间先后排列的序列,表示为
,其中
。
定义2 (情节):情节a是由若干事件类型组成的序列,记为
,其中
且对于所有的i和j (
)满足Ei总是列在Ej之前。情节a中事件类型的个数称为a的长度,记为|a|。长度为k的情节称为k-情节。
定义3 (子情节,超情节):给定情节a和b,若b中的事件类型均在a中出现,且先后顺序与a中的这些事件类型一致,则称b是a的子情节,或a是b的超情节,记为b Í a或a Ê b。
定义4 (前缀):设情节
,则称情节
是a的前缀。
定义5 (串接):给定情节a和b,将b的所有事件类型按其顺序列在a后面形成的新情节称为a和b的串接,记为concat(a,b)。
定义6 (发生):给定事件流S和情节
,若
是从S中删除若干事件后得到,且
,则称区间
为a在S上的一次发生,
为该发生的区间长度,t1为该发生的起始时间,tk为该发生的终止时间。
定义7 (最小发生):设
是情节a在事件流S上的一次发生,若S上不存在a的另一次发生
,使得
且
,或
且
,即
,则称
是a在S上的一次最小发生。情节a在事件流S上的所有最小发生组成的集合记为a.mo。
定义8 (最小且非重叠发生):设
和
是情节a在事件流S上的两次最小发生,且满足
或
,则称
和
是a在S上的最小且非重叠发生。情节a在事件流S上的所有最小且非重叠发生组成的最大集合记为a.mano。
定义9 (支持度):集合a.mano的基数|a.mano|称为情节a的支持度,记为a.sup。
定义10 (频繁情节):给定支持度阈值min_sup,若情节a的支持度大于等于min_sup,则称a是一个频繁情节。
2.2. 引理1:若b Í a,则b.sup ≥ a.sup
证明:因为b是a的子情节,则对于a.mano中a的任意两个最小且非重叠发生
和
,一定存在b的两个最小且非重叠发生
和
,满足
和
,这表明|b.mano| ≥ |a.mano|,即b.sup ≥ a.sup。引理1证毕。■
2.3. 定理1:非频繁情节的任何超情节也是非频繁的,频繁情节的任何子情节也是频繁的
定理1也称为情节单调性。
证明:由引理1和定义10可得证。■
2.4. 问题描述
给定事件流S和支持度阈值min_sup,问题描述为:设计一个挖掘S上所有频繁情节的算法,要求:1) 只需要单遍扫描S;2) 挖掘过程中不产生候选频繁情节;3) 尽可能少的时空需求。
3. 频繁情节挖掘算法MANEPI
3.1. 共享前缀树
由于许多频繁情节具有相同的前缀,为节省存储空间,算法采用共享前缀树存储频繁情节。共享前缀树SPT (Shared Prefix Tree)是一棵有向根树,树中的每个结点Na表示为一个四元组(label, mo, mano, children),其中:label为结点Na对应的事件类型,根结点的label为空,从根结点深度遍历到结点Na的路径上所有label的串接表示频繁情节a;mo为结点Na对应的频繁情节a的最小发生集,根结点的mo为空;mano为结点Na对应的频繁情节a的最小且非重叠发生集,根结点的mano为空;children为指向结点Na的孩子结点的指针,且这些指针按照所指孩子结点的label的字典序排列,所有叶结点的children为空。不难看出,SPT中非根结点对应的频繁情节是其所有孩子结点对应的频繁情节的前缀,共享前缀树由此而得名。
3.2. 算法MANEPI描述
算法MANEPI的基本思想是:首先单遍扫描给定事件流,从中发现所有频繁1-情节;然后对已发现的一个频繁i-情节a和一个频繁1-情节e进行串接,形成一个长度为i+1的新情节concat(a,e),这个过程称为以a为前缀的一次情节增长。若concat(a,e)的支持度小于给定的支持度阈值,则concat(a,e)为非频繁情节,由定理1可知,concat(a,e)的任何超情节也是非频繁的,因而就无须以concat(a,e)为前缀进行情节增长;反之,若concat(a,e)的支持度大于等于给定支持度阈值,则concat(a,e)为频繁情节,算法接着以concat(a,e)为前缀递归地进行下一次情节增长,整个算法的终止条件是没有任何情节可以增长。下面是MANEPI的伪代码。
AlgorithmMANEPI(S, min_sup)
Input: S: an event stream = <(E1,t1), (E2,t2), ∙∙∙, (En,tn)>;
min_sup: a support threshold
Output: SPT: a tree which stores all frequent episodes within S
1: Create SPT with simply a root node
2: Scan S once to find all frequent 1-episodes and Sort them in lexicographical order
3: For each frequent 1-episode edo
4: Create node Ne as a child of the root
5: For each frequent 1-episode edo
6: MineGrow (Ne)
Procedure Mine Grow (Na)
Input: Na: the node to be expanded
Objective: find all frequent episodes with prefix a
1: For each 1-episode e do
2: Let b = concat(a,e)
3: Let b.mo = ComputeMO(a,e)
4: Let b.mano = ComputeMANO(b)
5: If b.sup ≥ min_sup
6: Create node Nb as a child of Na
7: MineGrow(Nb)
3.3. 情节增长
MANEPI的核心是情节增长MineGrow,该过程的关键是如何计算一个新情节的支持度,具体而言,就是如何根据已发现的频繁i-情节a和频繁1-情节e来发现新情节concat(a,e)的所有最小且非重叠发生组成的最大集合。直观上,可以基于a.mano和e.mano来构造concat(a,e).mano。然而,由于在某些情形下a可能存在多个a.mano,无论选择哪一个a.mano,都有可能导致concat(a,e)的一些最小且非重叠发生丢失,从而也就不能发现所有的频繁情节。
例如,设S = <(A,1), (A,2), (B,3), (D,4), (A,5), (C,6), (B,7), (E,8), (A,9), (C,10), (B,11), (A,12), (C,13)>,a = ,e = ,b = concat(a,e),表1列出了基于S上所有可能的a.mano进行情节增长的两种情形。
从表1中可以看出,无论选择哪一个a.mano,都不能得到正确的b.mano,因为两种情形下的|b.mano|都等于1,但事实上|b.mano| = |{[1,3], [5,11]}| = 2,若min_sup = 2,则丢失了频繁情节b。可见,挖掘频繁情节时,若在SPT中只保存结点的mano,则不足以进行正确的情节增长,可能会导致部分频繁情节的丢失。为此,算法将情节增长分为两步实施:第一步,通过单遍扫描a.mo和e.mo得到concat(a,e).mo,这三个最小发生集均是唯一的;第二步,通过单遍扫描concat(a,e).mo得到最早出现的concat(a,e).mano。因为concat(a,e).mo保存了concat(a,e)的所有最小发生,所以由concat(a,e).mo得到的最早出现的concat(a,e).mano不会丢失concat(a,e)的任何最小且非重叠发生。由于a.mo和e.mo已将给定的事件流分割成有限个区间,所以基于这些有限的区间进行的情节增长避免了对给定事件流的多遍扫描。另外,SPT中每个结点的mano只是保存了指向该结点mo中相应最小发生的指针。下面是情节增长(包括两个子过程)的伪代码。
SubProcedure Compute MO(a,e)
Input: a: a frequent i-episode with its mo;
e: a frequent 1-episode with itsmo
Output: concat(a,e).mo: the moof concat(a,e)
1: Letconcat(a,e).mo = f
2: Let i = 1
3: For each occurrence [t′s, t′s]Îe.mo do
4: Starting from i, find the first index j of a.mos.t. [tjs, tje] Î a. mo and tje < t′s and t(j+1)e > t′s
5: Append [tjs, t′s] to concat(a,e).mo
6: Let I = j
7: Return concat(a,e).mo

Table 1. Two cases of episode growth
表1. 情节增长的两种情形
SubProcedure Compute MANO(b)
Input: b: an episode with its mo
Output: b. mano: the earliest mano of episode b
1: Let b. mano = {1}
2: Let i = 1
3: Let j = i + 1
4: While j < |b. mo| do
5: Find the first index k of b.mo after js.t. [tis, tie] Î b. mo and [tks, tke] Î b. mo and tie < tks
6: b.mano=b. mano
{k}
7: Let i = k
8: Let j = i + 1
9: Return b.mano
3.4. 算法MANEPI运行实例
设事件流S = <(A,1), (A,2), (B,3), (D,4), (A,5), (C,6), (B,7), (E,8), (A,9) (C,10), (B,11), (A,12), (C,13)>以及min_sup = 2。首先,MANEPI通过单遍扫描S,得到所有的频繁1-情节< A >、< B >和< C >,并在SPT中生成根结点的孩子结点N< A >、N< B >和N< C >;然后进行第一次情节增长,将已发现的频繁情节< A >与频繁1-情节< A >串接后形成新情节< AA >,通过调用ComputeMO和ComputeMANO得到< AA >.sup = |{[1, 2], [5, 9]}| = 2 ≥ min_sup,在SPT中生成结点N< A >的孩子结点N< AA >;接着,进行第二次情节增长,将已发现的频繁情节< AA >与频繁1-情节< A >串接后形成新情节< AAA >,得< AAA >.sup = |{[1, 5]}| = 1 < min_sup,因此,无须以< AAA >为前缀进行情节增长,算法返回至上一层,将已发现的频繁情节< AA >与频繁1-情节< B >串接后形成新情节
,∙∙∙;;最后,在S上发现了如
表2所示的18个频繁情节,挖掘过程中产生的共享前缀树如
图1所示。
3.5. 算法MANEPI正确性证明
引理2. 给定最小发生集的情节a和e,过程ComputeMO能够正确计算新情节concat(a,e)的最小发生集。
证明:对于e.mo中的每一个发生
(第3行),ComputeMO通过单遍扫描e.mo查找一个最大的j(第4行)满足[tjs, tje] Î a.mo且
且
,若不存在这样的j,则停止扫描e.mo。因
是a出现在e的发生
之前的最后一次发生,故
是concat(a,e)的一次最小发生,concat(a,e).mo是concat(a,e)的所有最小发生组成的集合。引理2证毕。■
引理3. 给定最小发生集的情节b,过程ComputeMANO能够正确计算b最早出现的所有最小且非重叠发生组成的最大集合。
证明:

Figure 1. The shared prefix tree for frequent episodes within S
图1. S上的频繁情节共享前缀树

Table 2. All frequent episodes with S
表2. S上的频繁情节
1) 过程ComputeMANO首先将b.mo中第一个发生[t1s, t1e]的索引号i(i = 1)添加至b.mano中(第1行),然后从索引号j = i + 1开始(第4行)单遍扫描b.mo,以查找最小的k(第5行)满足[tis, tie] Î b.mo且tie < tks,即查找b的第一个与[tis, tie]非重叠的发生[tks, tke],若不存在这样的k,则停止扫描b.mo。由于每次添加至b.mano中的发生(第6行)均与当前b.mano中的最后一次发生非重叠,所以最终的b.mano应是b最早出现的所有非重叠发生组成的集合。
2) 由引理2知,b.mano是b的最小发生集。
综合1)和2),引理3证毕。■
引理4:对于已发现的频繁情节a,过程MineGrow能够正确发现所有以a为前缀的频繁情节,并在SPT中生成相应的结点。
证明对于频繁情节a,过程MineGrow根据引理2和引理3,进行以a为前缀的一次情节增长(第2-4行),若concat(a,e)是非频繁的,则不在SPT中生成相应的结点,根据定理1,concat(a,e)的所有超情节也是非频繁的,过程MineGrow将以a为前缀进行下一次情节增长(第1行);若concat(a,e)是频繁的,则在SPT中生成相应的结点(第6行),并以concat(a,e)为前缀进行一次情节增长(第7行),如此迭代结束后,能够发现所有以a为前缀的频繁情节,并在SPT中生成相应的结点。引理4证毕。■
引理5:给定事件流S和支持度阈值min_sup,算法MANEPI能够正确发现S上的所有频繁情节,并在SPT中生成相应结点。
证明MANEPI首先单遍扫描S发现所有频繁1-情节(第1行),然后对每个频繁1-情节进行如下处理:在SPT中生成相应结点,并以该情节为前缀进行情节增长(第2~6行)。由引理4知,MANEPI最终能够发现所有频繁情节,并在SPT中生成相应结点。引理2.5得证。■
3.6. 算法MANEPI复杂度分析
设S为L个事件组成的事件流,e为S上的事件类型集,FE为S上的所有频繁情节组成的集合,sup_max为所有频繁1-情节的最大支持度,则算法MANEPI的复杂度分析如下:
定理2:MANEPI的时间复杂度为O(|FE| · |e| · L)。
证明:对于FE中的每个频繁情节a和e中的每个频繁1-情节e,旨在找到最早出现的concat(a,e).mano的情节增长操作是MANEPI的主要时间代价。完成一次情节增长只需单遍扫描a.mo和e.mo,其时间复杂度为O(L)。由定理1可知,MANEPI只需以FE中的每个情节为前缀进行情节增长,增长的次数为频繁1-情节的个数,其上界为|e|,因此,算法MANEPI完成全部的情节增长操作所需的时间复杂度为O(|FE| ∙ |e| · L)。定理2证毕。■
定理3:MANEPI的空间复杂度为O(sup_max · |FE|)。
证明算法MANEPI共发现了|FE|个频繁情节,而每个频繁情节至多有sup_max个最小且非重叠的发生,故算法所需的空间复杂度为O(sup_max · |FE|)。定理3证毕。■
4. 实验评估
本文通过七组实验来评估算法MANEPI。实验对比了MANEPI和经典算法MINEPI [1] 和NONEPI [12] 的运行时间、内存开销和挖掘质量。实验的硬件环境为3.6 GHz Intel(R) Core(TM) i7-4790 CPU,内存8 GB,操作系统为Windows 8,程序采用VC++ 6.0实现。
4.1. 数据集
我们选用CNKI的一个Web服务器上从2017年11月1日至2017年11月30日的日志数据,该日志数据包括了相关读者对156259种不同文献的207498个阅读记录。
4.2. 实验结果
实验1:运行时间vs支持度阈值通过改变支持度阈值,得到如图2所示的三个算法在数据集上的运行时间(以毫秒为单位)。
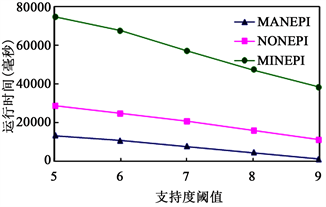
Figure 2. Averageruntime vs. min_sup
图2. 运行时间vs支持度阈值
可以看出,随着支持度阈值的减小,三个算法的运行时间都线性增加,导致上述事实的主要原因是:MANEPI采用了深度优先搜索策略,而MINEPI和NONEPI采用了广度优先搜索策略。
实验2:运行时间vs序列长度选择数据集上前6天、前12天、前18天、前24天的事件作为四个序列,设定支持度阈值为7,得到如图3所示的序列长度对算法时间性能的影响。
可以看出,三个算法的运行时间都随着序列长度的增加而线性增加,且它们的时间性能对比结果同实验1,导致这些现象的原因与实验1的解释相同。
实验3:内存开销vs支持度阈值通过改变支持度阈值,得到如图4所示的三个算法在数据集上的内存开销(以KB为单位)。
可以看出,随着支持度阈值的减小,三个算法的内存开销都线性增加,导致这些现象的原因与实验1的解释相同。
实验4:内存开销vs序列长度设定支持度阈值为7,得到如图5所示的序列长度对三个算法内存开销的影响。
可以看出,三个算法的内存开销都随着序列长度的增加而线性增加,且MANEPI的空间性能优于MINEPI和NONEPI,导致这些现象的原因与实验1的解释相同。
实验5:频繁情节个数vs支持度阈值通过改变支持度阈值,得到如图6所示的算法发现的频繁情节个数。
可以看出,随着支持度阈值的减小,MANEPI和MINEPI均发现了更多的频繁情节,这是因为在同一事件流上,支持度阈值越小,满足支持度阈值要求的频繁情节就越多。同时,可以观察到在同一事件流上MINEPI挖掘的频繁情节要多于MANEPI,这一现象也证实了MINEPI容易导致情节发生“过计数”问题,原因在于MINEPI基于最小发生来计算一个情节的支持度,而MANEPI基于最小且非重叠发生来计算一个情节的支持度。
实验6:频繁情节个数vs序列长度设定支持度阈值为7,得到如图7所示的序列长度对MANEPI和MINEPI发现频繁情节个数的影响。
可以看出,随着序列长度的增加,两个算法发现了更多的频繁情节,这是因为在同一支持度阈值下,事件流越长,满足支持度阈值要求的频繁情节就越多。同时,我们也观察到与实验5相同的另一现象,解释原因同实验5。
实验7:平均区间长度vs情节长度我们使用平均区间长度来评估算法的挖掘质量。所谓平均区间长度,是指相同长度频繁情节的所有发生区间的平均值,该值越小,越能体现一个情节中事件类型之间的紧随关系,挖掘的质量也就越高。设定支持度阈值为7,得到如图8所示的情节长度对MANEPI和NONEPI的平均区间长度的影响。

Figure 3. Averageruntime vs.sequence length
图3. 运行时间vs序列长度

Figure 4. Average memory vs. min_sup
图4. 内存开销vs支持度阈值

Figure 5. Average memory vs. sequence length
图5. 内存开销vs序列长度

Figure 6. Number of frequent episodes vs. min sup
图6. 频繁情节个数vs支持度阈值
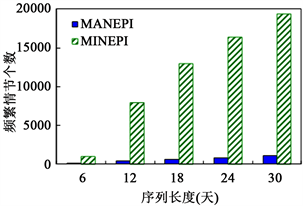
Figure 7. Number of frequent episodes vs. sequence length
图7. 频繁情节个数vs序列长度

Figure 8. Average interval vs. episode length
图8. 平均区间长度vs情节长度
可以看出,随着情节长度的增加,两个算法的平均区间长度也在增加。同时,MANEPI的挖掘质量高于NONEPI,这是因为NONEPI所考虑的非重叠发生未必是最小发生,挖掘的频繁情节并不能很好地描述一个情节中事件类型之间的紧随关系,下面举例说明这个问题。
<基于隐马尔可夫模型的多步攻击预测研究,面向分布数据安全的误用检测算法和入侵检测系统的研究,隐马尔可夫模型在入侵检测中的应用,基于入侵响应的入侵警报关联性的攻击预测算法,基于因果网络的攻击计划认别与预测,面向网络安全的基于入侵事件的早期预警方法>是算法MANEPI及NONEPI均能发现的一个频繁6-情节,该情节刻画了读者如下的行为模式:
旨在研究一个基于隐马尔可夫模型的攻击预测方法(见第一篇阅读文档),这些读者首先理解了两种常用的入侵检测模型,即误用检测模型(见第二篇阅读文档)和异常检测模型(见第三篇阅读文档),然后分析了现有攻击方法的不足(见后三篇阅读文档)。
由算法MANEPI和NONEPI得到的该情节的平均区间长度分别是180分钟和300分钟,即表示大多读者完成上述6篇文献的阅读分别需要3小时和5小时左右。显然,MANEPI的挖掘结果更有助于CNKI向读者提供个性化的文献阅读推荐服务。
5. 结束语
本文提出了一个采用深度优先搜索策略和共享前缀树存储结构的频繁情节挖掘算法MANEPI,该算法只需单遍扫描给定的事件流,且挖掘过程不产生候选频繁情节。实验评估表明算法MANEPI具有较好的时空性能和较高的挖掘质量,挖掘结果能够揭示读者的阅读习惯和预测读者的阅读倾向,从而有助于数字图书馆向读者提供更好的个性化服务。未来我们将研究能够融合多种支持度定义的频繁情节挖掘算法。
基金项目
本文受江苏省自然科学基金(BK20141307),江苏省“333工程”基金(BRA2015212),教育部“云数融合科教创新”基金(2017B06109),江苏省“大创”基金(201712917007Y)资助。