基于随机森林模型的湫水河流域洪水过程模拟

Random Forests Model Based Flood Process Simulation in the Qiushui River Basin

摘要: 黄河中游干旱半干旱地区洪水预报精度水平普遍不高，其主要原因在于降雨时空高度变异性以及大范围水土保持措施对产汇流的强烈干扰。随着现代统计理论发展，智能机器学习算法为该地区洪水预报提供了新的途径。以黄河中游左岸湫水河流域为例，采用随机森林算法建立暴雨洪水预报模型，对汛期场次洪水过程进行模拟，结果表明：当计算时间步长为1小时，随机森林模型的确定性系数(NSE)平均值为0.47，以NSE ≥ 0.60衡量，合格率为42%；当计算时间步长为0.5小时，NSE平均值为0.76，场次洪水预报合格率为88%；由此可知，输入资料精度是决定模型精度的主要因素。此外，不同时间步长条件下，随机森林模型的应用效果均明显优于传统的多元回归统计模型，表明随机森林模型适用于湫水河流域的洪水过程预报，对黄河中游黄土高原地区防洪预警具有一定参考价值。

Abstract: The accuracy level of flood forecasting in arid and semi-arid areas of the middle Yellow River region is generally not high, which is mainly due to the spatial and temporal variability of rainfall and the inten-sive disturbances of large-scale soil and water conservation measures on the runoff production and routing processes. With the development of modern statistical theory, intelligent machine learning algorithms provide a new way for flood forecasting in this region. Taking the Qiushui River Basin on the left bank of the middle reaches of the Yellow River as an example, the random forest algorithm was used to establish the storm-flood forecasting model and simulate the rainfall-runoff during the flood season. The results showed that when the calculation time step was 1 hour, the average value of the Nash-Sutcliffe efficiency (NSE) of the Random Forest model was 0.47, and the qualified rate was 42% when NSE ≥ 0.60 was measured. When the calculation time step was 0.5 hours, the average NSE value was 0.76, and the corresponding qualified rate increased to 88%. Therefore, the accuracy of the input data was a main factor affecting the model accuracy in this region. In addition, under different time steps conditions, the performance of the Random Forest model is obviously better than that of the traditional multivariate regression statistical model, indicating that the random forest model is suitable for flood process prediction in the Qiushui River basin, and has a certain reference value for the flood warning in the Loess Plateau in the middle reaches of the Yellow River.

1. 引言

洪水灾害往往会给人民群众的生产生活带来大量的损失，造成严重后果，因此作出准确的实时洪水预报预警具有重大意义。在现代电子计算机和通信等技术的发展下，实时洪水预报系统也在进一步发展，预报精度得到大幅提高 [1] 。在黄河中游黄土高原干旱半干旱地区，暴雨强度大、历时短，多表现为超渗产流模式，形成的洪水突发性强、水量集中、破坏力大 [2] ，对当地国民经济和人民生命财产安全造成严重危害。一直以来，干旱半干旱地区的水文预报始终是水文科学的难题，理论进展缓慢 [3] 。特别对黄土高原地区，由于其特殊的地形地貌条件，给传统的水文模型的应用带来困难 [4] 。近些年来，随着人水和谐理念的贯彻和生态文明建设的推进，黄河中游地区建设了大量的淤地坝、小型塘坝、梯田、林草地等水土保持措施，一定程度上改变了洪水的形成条件，产汇流规律出现一些新的变化，给流域洪水预报带来更大的挑战 [5] [6] 。随着大数据概念兴起 [7] [8] ，借助于智能算法、数据挖掘、深度学习等大数据分析技术，可从海量历史数据中发现隐含的降雨径流因果关系或水文规律，从而实现水文过程的预报预测，为水文预报提供了新的途径 [9] [10] [11] 。

随机森林(Random Forests)模型是Leo Breiman于2001年提出了一种数据挖掘技术，其本质是Bagging集成学习理论与随机子空间相结合的一种分类器组合方法 [12] 。该方法作为一种分类回归智能算法，预测的准确率很高，可克服决策树过拟合问题，对噪声和异常值有较好的容忍性，对高维数据分类问题具有良好的可扩展性和并行性，因而在生物信息、医学研究、商业管理、语言建模、经济金融等领域已取得了不错的结果 [5] ，对水文预报也具有较大的研究价值和应用前景 [13] [14] [15] 。本文选择黄河中游黄土高原湫水河流域为研究区，构建基于随机森林的洪水预报模型，开展汛期场次洪水过程模拟，检验模型的适用性。

2. 随机森林方法介绍

随机森林是一种集成机器学习方法，它利用随机重采样技术Bootstrap和节点随机分裂技术构建多棵决策树，通过投票得到最终分类结果。由图1可知，随机森林主要分为训练样本子集和子分类模型两部分，训练样本子集从原始训练集(预报因子数据)中通过简单随机抽样(Bootstrap随机抽样)的方式获取，子分类模型一般为决策树算法；多个子分类模型可得到多个分类结果，然后通过对每个子分类模型的预测值进行投票(预报对象为分类变量时)或取平均值(预报对象为连续数值变量时)来决定最终预测值。

随机森林方法中的关键技术主要包括Bagging集成学习法和决策树分类法：

1) Bagging是根据统计中Bootstrap思想提出的一种集成学习算法，它从原始样本集中可重复抽样得到不同的Bootstrap训练样本，进而训练出各个基本分类器，以保证各个训练样本子集的差异性。对于决策树等不稳定(即对训练数据敏感)的分类器，Bagging算法能提高分类的准确度。此外，Bagging算法可以并行训练多个基本分类器，可以节省大量的时间开销，这也是该算法的优势之一。

2) 决策树(Decision Tree)是用于分类和预测的主要技术，它着眼于从一组无规则的事例推理出决策树的表示形式的分类规则。它利用树的结构将数据记录进行分类，树的一个叶节点(预报因子)就代表某个条件下的一个记录集，根据记录字段的不同取值建立树的分支；在每个分支子集中重复建立下层节点和分支，得到最终分类结果。基于决策树算法的一个最大的优点是，它在学习过程中不需要使用者了解很多背景知识，只要训练事例能够用属性即结论的方式表达出来，就能使用该算法进行学习。

将随机森林算法应用于水文预报时，由预报因子与预报对象的历史观测数据可构建随机森林模型；在模型预测阶段，只要将最新观测的预报因子数据输入到模型中，便可得到预报对象的预测值。

3. 实例应用

3.1. 流域概况

湫水河流域是黄河中游河龙区间的一级支流，河长121.9 km，流域面积为1989 km²，流域把口站为林家坪水文站，距河口距离13 km，控制面积1863 km²。该流域地处黄土高原典型半湿润半干旱区，多年平均降水量约500 mm，降雨迅猛而短暂，洪水多发，加之河床坡度陡，使得洪水历时短、洪峰大、洪水过程陡涨陡落。湫水河流域雨量站与水文站分布见图2，共8个雨量站、1个水文站。本次研究选择1980~2011年间汛期26场洪水过程资料，检验随机森林模型在场次洪水过程模拟中的适用性；其中20场洪水用于模型率定，6场用于模型验证，时间步长为0.5小时和1小时。

3.2. 模型构建

将场次洪水的累积i小时流域面平均降雨量(i = 0.5, 1.0, 1.5, , 6)和提前j小时的本站(林家坪站)流量(j = 0.5,1.0, 1.5)作为初选预报因子(自变量)，将逐时段洪水流量作为预报对象(因变量)，以相关系数为目标函数，根

Figure 1. Model structure of Random Forests

图1. 随机森林模型结构图

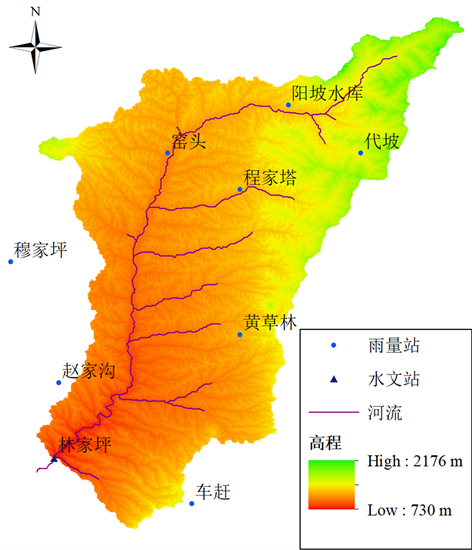
Figure 2. River network, rain gauges and hydrological station

图2. 湫水河流域水系及站网分布

据统计分析筛选预报因子。

在预报时刻t，当计算时间步长ΔT = 1 h时，筛选的预报因子为：①提前6 h的累积雨量P_t-6，②提前4 h的累积雨量P_t−4，③提前1 h的流量Q_t−1；当计算时间步长ΔT = 0.5 h时，筛选的预报因子为：①提前6 h的累积雨量P_t−6，②提前4 h的累积雨量P_t−4，③提前0.5 h的流量Q_t−0.5。随机森林模型选用Matlab软件中随机森林工具箱，决策树数量为100，其他参数选用默认参数。

为作比较，将同时构建林家坪站洪水预报的多元回归统计模型。当计算时间步长ΔT = 1 h时，预报时刻t林家坪站流量Q_t为：

$Q_t=18.53672P_{t-}{}_4+2.358017P_{t-}{}_6+0.482646Q_t{}_{-1}+7.106008$ (1)

当计算时间步长ΔT = 0.5 h时，预报时刻t林家坪站流量Q_t为：

$Q_t=13.39398P_{t-}{}_4+1.591412P_{t-}{}_6+0.799825Q_t{}_{-0.5}-0.47429$ (2)

式中，雨量单位为mm，流量单位为m³/s。

3.3. 结果分析

3.3.1. 计算时间步长ΔT = 1 h

根据《水文情报预报规范(GB/T22482-2008)》的规定，采用相关系数、确定性系数、洪峰相对误差、洪量相对误差及峰现时间误差5种评定指标分别对率定期20场洪水和验证期6场洪水模拟过程进行精度评定。当ΔT = 1 h时，随机森林模型的率定期20场洪水和验证期6场洪水的精度统计结果如图3所示，率定期和验证期均仅有一场洪水的相关系数低于0.6，平均值分别为0.82和0.77；根据确定性系数统计，率定期和验证期分别有多达11场和4场洪水低于0.6，结果较差；在洪峰、洪量误差指标方面，模型模拟结果不好，最大绝对值误差分别达到65%和86%；峰现时间误差指标精度较高，仅有一场洪水(#2010091907)的误差为+6 h，其他场次均在允许误差±3 h以内。

作为对比，根据多元回归统计模型(ΔT = 1 h)计算的结果精度统计见图4，结果表明：就峰现时间误差而言，多元回归模型的结果要明显优于随机森林模型；在相关系数、洪峰误差及洪量误差3个指标上两个模型精度基本相当；但多元回归模型的确定性系数指标则比随机森林模型的低很多。

3.3.2. 计算时间步长ΔT = 0.5 h

当时间步长减小为0.5 h时，随机森林模型的精度大幅度提升，在5个精度评定指标上均优于时间步长为1 h的结果，见图5；所有场次洪水的相关系数均大于0.69，平均值高达0.9；确定性系数低于0.6的洪水场次由原来的15场减少为3场；洪峰、洪量误差的平均绝对值分别由32.5%、25.2%降低为16.7%、13.6%；在峰现时间误差指标上，则仍有一场洪水(#2011070215)的误差(+6 h)不满足精度要求。

同样地，当模型计算时间步长减小时，多元回归模型的精度也得到显著提高，但仍低于ΔT = 0.5 h的随机森林模型结果，在5个性能指标上均有所体现(见图6)。

3.3.3. 模型精度对比

在洪水过程预报中，确定性系数是衡量模型结果好坏的关键指标，因此表1给出了随机森林模型和多元回归统计模型在两种计算时间步长条件下的确定性系数结果进行对比。以确定性系数大于0.6为标准，随机森林模型(ΔT = 1 h, ΔT = 0.5 h)与多元回归模型(ΔT = 1 h, ΔT = 0.5 h)在所有洪水场次中模拟结果合格的分别为11场、23场、8场和22场；可以看出，在相同时间步长条件下，随机森林模型结果要优于多元回归统计模型；当时间

Figure 3. Model performance of Random Forests when time step = 1 hour

图3. 随机森林模型模拟结果精度统计(ΔT = 1 h)

Figure 4. Model performance of multiple regression model when time step = 1 hour

图4. 多元回归统计模型模拟结果精度统计(ΔT = 1 h)

Figure 5. Model performance of Random Forests when time step = 0.5 hour

图5. 随机森林模型模拟结果精度统计(ΔT = 0.5 h)

Figure 6. Model performance of multiple regression model when time step = 0.5 hour

图6. 多元回归统计模型模拟结果精度统计(ΔT = 0.5 h)

Table 1. Nash-Sutcliffe efficiency coefficient results of two models at different time steps.

表1. 随机森林模型与多元回归统计模型在不同时间步长下计算的确定性系数结果

Continued

步长由1 h减小为0.5 h时，模型精度有大幅度提高，两种模型的场次合格率基本相当。这说明在半干旱的黄土高原湫水河流域，资料精度是制约模型预报结果好坏的主要因素；当计算时间步长较大时，资料均化处理的误差将会明显降低洪水预报精度。

4. 小结

采用数据挖掘手段，筛选关键预报因子，构建了基于随机森林的洪水预报模型，应用于黄河中游黄土高原地区的湫水河流域。通过1980~2011年间汛期26场洪水的模拟分析，结果表明：随机森林模型在黄河中游半干旱流域具有一定适用性，模型精度要明显高于传统的多元回归统计模型；当计算时间步长由1 h降低为0.5 h时，模型确定性系数将有显著提高。

基金项目

国家重点研发计划课题(2016YFC0402706)，国家自然科学基金面上项目(41877147)，水利部公益性行业科研专项(201501004)，大学生创新创业训练项目(2017102941033)。