多个对数正态总体共同均值的估计问题研究

Research on the Estimation of Common Mean for Multiple Log-Normal Populations

摘要: 若随机变量 X=lnY～N(µ，σ²), 则随机变量 X 服从对数正态分布，对数正态分布用来表示一类正右偏数据，实际应用非常广泛[1]。在很多情况下，数据的来源有不同的背景，对于单个总体的研究[2]已经不能满足我们的需求，此时的主要目的是基于几个总体来研究他们的共同参数问题。本文对于单个样本利用广义推断的方法给出均值[3]广义枢轴量，然后基于每个总体所抽取的样本量和近似样本方差的广义枢轴量给出不同总体共同均值的广义枢轴量的加权平均，得到共同均值的广义置信区间，利用R语言进行数值模拟，得到的覆盖概率接近置信水平。

Abstract: If the random variable  X=lnY～N(µ，σ²) , then the random variable X follows the log-normal distribution, which is used to describe a class of positive right-skewed data and the practical ap-plication is very extensive [1]. In many cases, the source of data has different backgrounds, for a single population research [2] has been unable to meet our needs, so the main purpose of this time is to study their common parameters based on several populations. In this paper, the generalized pivot of the mean [3] is given for a single sample by means of generalized inference, and then the weighted average of the generalized pivot is given for different populations of common mean based on the sample size extracted from each population and the generalized pivot of approximate sample variance. Then the generalized confidence interval of the common mean is obtained. The probability of coverage is close to the confidence level using R.

1. 引言

当某一测量值受多种因素的随机影响时，该值常呈对数正态分布，对数正态分布在实际中有着重要的应用，例如它主要被广泛的用于描述如在金融市场的理论研究中，著名的期权定价公式以及许多实证研究都用对数正态分布来描述金融资产的价格。另外在工程、医学和生物学领域里对数正态分布也有着广泛的应用，很多研究都会用它来拟合寿命数据以及人口收入数据。往往人们会得到不同背景下的服从对数正态分布的数据，对于这些有着共同均值的不同总体，我们会充分利用他们之间的信息，来估计共同均值，这就是本文所研究的内容。

2. 广义枢轴量和广义置信区间

定义1：对数正态分布

若随机变量 $X=\ln Y~N\left(\mu ,{\sigma }^2\right)$ ，则随机变量 $Y$ 服从两参数的对数正态分布，其密度函数为：

$f\left(y\right)=f\left(y\right)=\{\begin{array}{c}\frac{1}{\sqrt{2\pi }\sigma y}{\text{e}}^{-{\left(\ln y-\mu \right)}^2/2{\sigma }^2}\\ 0\end{array}\begin{array}{c}y>0\\ y\le 0\end{array}$

其均值 $EY=\exp \left(\mu +{\sigma }^2/2\right)$ 。

2.1. 广义枢轴量和广义置信区间

定义2：广义枢轴量和广义置信区间

形如 $R\left(X;x,\eta \right)$ 的广义枢轴量是X，x和 $\eta$ 的参数，其中 $\eta =\left(\theta ,\delta \right)$ ， $\theta$ 是兴趣参数， $\delta$ 是讨厌参数，并且满足以下条件：

1) 对给定的 $x$ ， $R\left(X;x,\eta \right)$ 的分布与未知参数 $\eta =\left(\theta ,\delta \right)$ 无关；

2) 观测值 $r=R\left(x;x,\eta \right)$ 与讨厌参数 $\delta$ 无关。

假设给定广义枢轴量 $R\left(X;x,\eta \right)$ 和置信系数 $\gamma \left(0<\gamma <1\right)$ ，寻找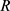的样本空间的一个子集 $C_{\gamma }$ ，使得

$P\left(R\left(x;x,\eta \right)\in C_{\gamma }\right)=\gamma$

取

${\Theta }_{\gamma }=\left\{\theta |R\left(x;x,\eta \right)\in C_{\gamma }\right\}$

则称 ${\Theta }_{\gamma }$ 为参数 $\theta$ 的一个置信系数为 $\gamma$ 的广义置信区间。

广义枢轴量法解决了传统枢轴量法无法解决的问题，即当分布含有讨厌参数时枢轴量很难或者无法构造的问题。

事实上，广义检验变量 $T$ 和广义枢轴量 $R$ 之间有如下关系：

$T+R=g\left(\theta \right)$ ，其中 $g\left(\theta \right)$ 为兴趣参数的函数，因此可以通过构造广义枢轴量的方法来进行假设检验，且其相应的广义 $p$ 值可以通过二者的关系计算得到。

2.2. Fiducial广义枢轴量

定义3：Fiducial广义枢轴量

设 $R\left(X;x,\eta \right)$ 是关于X，x和 $\eta$ 的参数，其中 $\eta =\left(\theta ,\delta \right)$ ， $\theta$ 是兴趣参数， $\delta$ 是讨厌参数，并且满足以下条件：

1) 对给定的 $x$ ， $R\left(X;x,\eta \right)$ 的分布与未知参数 $\eta =\left(\theta ,\delta \right)$ 无关；

2) 观测值 $R\left(x,x,\eta \right)=\theta$ 。

则称 $R\left(X,x,\eta \right)$ 为兴趣参数 $\theta$ 的Fiducial广义枢轴量。

可以看出Fiducial广义枢轴量是广义枢轴量的特殊情况，这也使得Fiducial广义枢轴量可以通过构造参数的Fiducial分布得到，且已经有了较为成熟的构造方法，下面的部分将主要通过实例来做假设检验问题。

3. 提出的方法

3.1. 广义枢轴量的构造

考虑 $k$ 个独立的有公共均值 $\theta =\exp \left(\mu +{\sigma }^2/2\right)$ 的对数正态总体。令 $Y_{i1},Y_{i2},\cdots ,Y_{1ni}$ 是从第 $i$ 个对数正态总体中抽取的随机样本，且有：

$X_{ij}=\log Y_{ij}~N\left({\mu }_i,{\sigma }_i^2\right)$ ，因此我们有：

$\theta =\exp \left({\mu }_i+{\sigma }_i^2/2\right)$ ， $i=1,2,\cdots ,k$ 。

令 ${\bar{X}}_i$ 和 $S_i^2$ 分别表示从第 $i$ 个对数正态总体样本数据做对数转换后的均值与方差， $X_{ij}=\log Y_{ij}\left(j=1,2,\cdots ,n_i\right)$ ，且令 ${\bar{x}}_i$ 和 $s_i^2$ 分别表示他们的观测值。由于：

$\frac{{\bar{X}}_i-{\mu }_i}{\sqrt{{\sigma }_i^2/n}}=Z_i~N\left(0,1\right)$

$\left(n_i-1\right)S_i^2/{\sigma }_i^2=V_i~{\chi }_{n_i-1}^2$

其中 $Z_i$ 是服从标准正态分布的随机变量， $V_i$ 是服从自由度为 $n_i-1$ 的卡方分布的随机变量，且两者相互独立。因此可以构造广义枢轴量：

$R_{{\sigma }_i^2}=\frac{\left(n_i-1\right)s_i^2}{V_i}$ ， (1)

$R_{{\mu }_i}={\bar{x}}_i-\frac{Z_i}{\sqrt{U_i}}\sqrt{\frac{\left(n_i-1\right)s_i^2}{n_i}}$ (2)

因此 $R_{\theta }^{\left(i\right)}=\exp \left(R_{{\mu }_i}+\frac{R_{{\sigma }_i^2}}{2}\right)$ (3)

对于第 $i$ 个总体，其极大似然估计为 ${\hat{\theta }}^{\left(i\right)}=\exp \left({\hat{\mu }}_i+\frac{{\sigma }_i^2}{2}\right)$ [4] ， (4)

其中 $$ ， ${\hat{\sigma }}_i^2=S_i^2$ 。

${\hat{\theta }}^{\left(i\right)}$ 的样本方差可以近似为：

$\mathrm{var}\left({\hat{\theta }}^{\left(i\right)}\right)={\sigma }_i^2\left(1+{\sigma }_i^2/2\right)\exp \left(2{\mu }_i+{\sigma }_i^2\right)$ [5] (5)

从而我们所研究的对数正态的均值 $\theta$ 的广义枢轴量是基于 $k$ 个广义枢轴量 $R_{\theta }^{\left(i\right)}$ 的加权平均值，具体形式如下：

$R_{\theta }=\frac{{\displaystyle {\sum }_{i=1}^k{R}_{w_i}{R}_{\theta }^{\left(i\right)}{n}_i}}{{\displaystyle {\sum }_{i=1}^k{R}_{w_i}{n}_i}}$ ， (6)

其中： $R_{w_i}={1/R}_{\mathrm{var}\left({\theta }^{\left(i\right)}\right)}$ (7)

$R_{\mathrm{var}\left({\hat{\theta }}^{\left(i\right)}\right)}=R_{{\sigma }_i^2}\left(1+R_{{\sigma }_i^2}/2\right)\exp \left(2R_{{\mu }_i}+R_{{\sigma }_i^2}\right)$ (8)

3.2. 算法

对给定的观测值：

1) 计算 ${\bar{x}}_i$ 和 $s_i^2$ ， $i=1\cdots k$ 。

2) 产生 $V_i~{\chi }_{n_i-1}^2$ 的实现值，然后按(1)给出的公式计算 $R_{{\sigma }_i^2}$ ， $i=1\cdots k$ 。

3) 产生 $Z_i~N\left(0,1\right)$ 和 $U_i~{\chi }_{n_i-1}^2$ 的相互独立的实现值，然后根据(2)给出的公式计算 $R_{{\mu }_i}$ ， $i=1\cdots k$ 。

4) 根据公式(3)计算 $R_{\theta }^{\left(i\right)}$ ， $i=1\cdots k$ 。

5) 重复步骤2~3共 $t$ 次，根据公式(7)和(8)计算 $R_{w_i}$ 。

6) 根据公式(6)计算得到 $R_{\theta }$ 。

7) 重复步骤2~6共m次，得到一系列 $R_{\theta }$ 。

8) 将这以系列 $R_{\theta }$ 案从小到大排列。

通过得到的有序的 $R_{\theta }$ 数列，取其2.5%分位点与97.5%分位点，得到 $\theta$ 的置信水平为95%的置信区间。

4. 模拟研究与结论

在本次模拟实验中，取总体个数为2个，样本量分别为 $n_1=20,n_2=40$ ，作了对数变换后的数据的总体均值我们定，为 ${\mu }_1/{\mu }_2=5/3$ 和 $10/3$ ，共同均值 $\psi =\log \theta$ 的值取0.3，0.5，0.8，1.0，1.2，1.5和2.0。下面以表格的形式对比广义推断的方法与大样本方法得到的95%置信区间的覆盖率，见表1。

其中比率是两总体参数 $\mu$ 的比率： ${\mu }_1/{\mu }_2$ 。

Table 1. Empirical coverage probabilities of 90 percent two-sided confidence bounds for the common mean

表1. 共同均值θ的置信水平为95%的双侧置信区间的主要覆盖率

从上述结果来看，当样本量较小时，广义枢轴量的方法的真实覆盖水平明显高于大样本方法，显示出其良好的估计性能。当样本量逐渐增加时，大样本的优良效果逐渐明显，广义枢轴量的方法仍具有良好的性能。