1. 引言
空间变系数模型是线性模型适应空间数据的进一步推广,它将数据的地理位置引入回归系数中,以系数函数在空间位置处的估计值来分析回归关系的空间非平稳性特征,该模型满足了人们对处理空间问题的需要。
Brunsdon等 [1] 首次明确提出了空间变系数模型,同时给出了该模型的地理加权回归(geographical weighed regression,简称GWR)方法,即以观测点之间的距离函数为权值的非参数光滑估计方法。Wang Ning等 [2] [3] 将变系数模型的局部线性拟合方法推广到空间变系数模型的情况,给出了局部线性GWR方法。程鹏鹏 [4] 提出了局部非线性GWR拟合方法,在降低系数函数估计的偏和边界效应上较局部线性GWR方法更显著。LeSage [5] [6] 提出了贝叶斯地理加权回归(Bayesian geographical weighed regression,简称BGWR)模型,首先运用Gibbs抽样技术给出一组参数用来修正异常观测值,由贝叶斯公式得到待估参数的条件后验概率 [7] ,保证估计结果的稳健性,之后再根据GWR方法的原理进行估计。冯金杰 [8] 通过空间加权距离构造权重矩阵,基于多元线性回归模型的贝叶斯统计推断 [9] ,得到了该模型的局部线性BGWR估计方法。
本文在局部线性BGWR拟合方法的基础上,给出空间变系数模型的局部非线性BGWR估计方法,推导出各回归系数的满条件后验分布,采取Gibbs抽样方法得到模型参数的估计。通过模拟,将此方法的参数拟合结果可视化、计算偏差均值和标准差均值,并与局部非线性GWR估计方法的结果进行对比分析。
2. 空间变系数模型的局部非线性BGWR估计
本文的空间变系数自回归模型为:
(1)
令模型中的
是模型所包含得空间截距项,
,
,由泰勒公式知在
的邻域内
可进行二阶泰勒展开,并用u和v的二次函数作逼近,即有
(2)
其中
,
,
,
,
分别表示
关于u和v的一阶、二阶偏导数在
处的值。根据变系数模型的局部非线性拟合及GWR方法,选取未知参数
,
,
,
和
,使得:
(3)
达到最小,其中
分别为因变量Y和自变量
在地理位置
处的观测值,
为
到
的距离,
令
设计矩阵为
,其中:
则局部非线性GWR方法的系数函数估计值为:
(4)
于是有,
,因此似然函数为:
其中
。
若取
,
,那么由贝叶斯定理可知
,
,且参数
的满条件后验分布为:
(6)
其中自由度为
,位置参数为
,精度矩阵为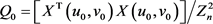 ,
,
方差
的满条件后验分布为:
(7)
其中形状参数为
,尺度参数是
。
3. 模拟试验
本模拟实验,指定一个正方形区域,以此区域左下角为坐标原点建立直角坐标系,将横、纵坐标进行
等分处理,以坐标系中每个点作为地理位置
,则样本容量为
。我们取
,有
,在如上建立的直角坐标系下,观测点地理位置坐标可表示为:
其中
表示
除以m的余数,
表示
除以m的商的整数部分。
从而用以产生数据的空间变系数模型为:
其中,自变量观测值
来自均匀分布
中的n个随机数,误差
来自正态分布
中的n个随机数。选取系数函数
和
:
在模拟实验中,选择高斯函数作为核函数,光滑参数h可使用CV准则来确定。根据已推出的参数的满条件后验分布,通过Gibbs抽样实现参数的
和
的估计,让
遍历所有位置,可得到所有点的系数估计值。
绘制出
,
的初值曲面图(如图1)和各回归系数函数在不同参数估计方法下的估计曲面图(如图2a,2b)。相比之下,局部非线性BGWR估计方法得到的系数曲面更接近原曲面的基本特征,而局部非线性GWR估计得到的曲面边界较为粗糙。因此,在对模型系数函数估计时,局部非线性BGWR估计方法更具精确性。
分别计算两种估计方法的绝对偏差MBias和均方误差MSE的值,结果如表1。不难发现,局部非线性BGWR方法估计相比局部非线性GWR方法的
和
的值要小一些,说明局部非线性BGWR方法估计系数函数估计的精确度相比较高。
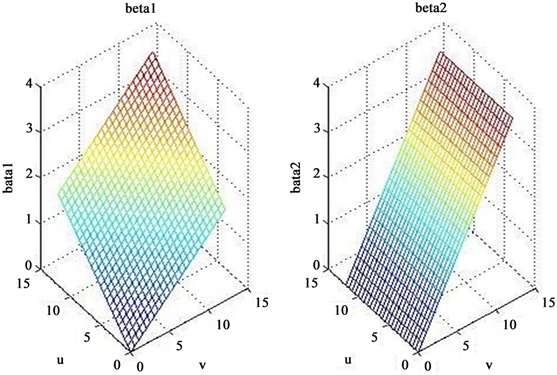
Figure 1. Surface map of the initial values of each coefficient function
图1. 系数函数初值曲面图
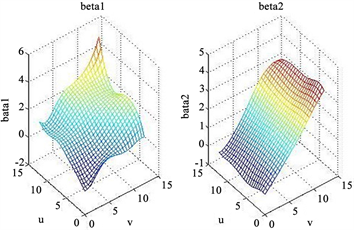
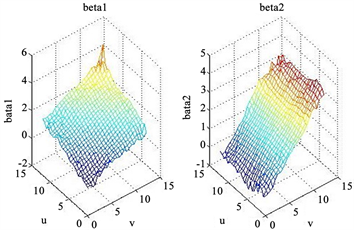 (a) (b)
(a) (b)
Figure 2. (a) Estimation of each coefficient function of the local nonlinear GWR fitting method, (b) Estimation of each coefficient function of the local nonlinear BGWR fitting method
图2. (a) 局部非线性GWR拟合方法的模型系数函数估计值,(b) 局部非线性BGWR拟合方法的模型系数函数估计值

Table 1. Absolute deviation and mean square error of the estimated
表1. 估计值MBias和MSE结果
4. 结论
本文基于对空间变系数模型的参数拟合方法研究的思想,结合局部非线性GWR方法和贝叶斯方法,提出局部非线性BGWR拟合方法,推导出各参数的满条件后验分布,采用Gibbs抽样技术得到模型的系数函数估计值。同时,本文设计模拟实验,通过可视化形式,展现出局部非线性BGWR和局部非线性GWR方法的参数拟合效果,结果显示,采用局部非线性BGWR方法估计的各估计值的绝对偏差、均方误差值和系数函数拟合图均优于局部非线性GWR参数拟合方法。
NOTES
*第一作者。
#通讯作者。