1. 引言
众所周知,序列密码算法中的密钥流序列一般可利用具有伪随机性的离散系统来产生,而离散混沌系统是用来产生伪随机序列的一种常用方法。考虑到离散时变双边广义符号混沌系统还没有文献研究过,本文将会研究这类特殊系统的混沌性及其在序列密码算法设计上的应用。
设
是一个双边整数集,
是一个单边整数集,对任一
。文献 [1] - [8] 讨论了多种时变或时不变单边离散时空系统。本文将讨论一类新的时变双边离散时空系统:
,
,
(1)
其中,I是实数集R的一个有界子集,多元函数
是系统(1)的系统函数。
显然,对任意
,存在一个离散时空序列
满足(1),且
,
。称x为系统(1)初值为
的一个解。参照文献 [5] ,当
时,将系统(1)称为(时变双边)广义符号动力系统,其中,
。
对于任一有界实数子集I,记
(2)
设
是系统(1)的一个解,
,
,且
,
(3)
则系统(1)等价于如下的无穷维离散系统
,
(4)
其中,该系统映射列
或
是由f决定或导出的
上的一列映射。
上面介绍了本文所要研究的离散时空系统的基本知识,后续内容安排如下:第2节将介绍与Devaney混沌相关的基本概念;第3节将会构造出一类具体的时变双边广义符号混沌系统,将对该系统解序列的伪随机性进行一些常见的仿真分析,并将对所构造的一种混沌序列密码算法进行仿真。
2. 几个定义
一般地,利用度量空间
上的一列映射
都能产生如下形式的时变离散系统
,
,
(5)
给定任一点
,都存在一个序列
满足(5)。将
称为系统(5)初值为
的一个解或映射列
的一条轨道。对任意
和
,记
,
(6)
对任一有界实数集I,设
由式(2)定义。可定义如下度量
而得到度量空间
:
,对任意
(7)
下面将给出一列映射与混沌相关的几个概念,可参见文献 [4] [5] [6] 。
定义1. 如果
的一条轨道
是周期性的,即存在正整数p,使得
,
,则称
为G或系统(5)的周期点,称p为
或
的周期。如果G的所有周期点组成的集合在X中是稠密的,则称G或系统(5)具有周期点的稠密性。
定义2. 对于度量空间
上的一列映射
,如果对X的任意两个非空开子集U和V,都存在正整数n,使得
不是空集,则称
或系统(5)具有传递性。
另外,如果存在
,使得对任意
和x的任一邻域U,都存在一个正整数m和
,使得
,则称
或系统(5)具有对初值的敏感依赖性。
定义3. 称度量空间
上的一列映射
或时变离散系统(5)在Devaney意义下是混沌的,简称为Devaney混沌,如果1) G或系统(5)具有传递性;2) G或系统(5)具有周期点的稠密性;(iii) G或系统(5)具有对初值的敏感依赖性。
定义4. 设I是有界实数集,
是一个四元函数,且
是由系统(1)所导出的度量空间
上的一列映射。如果系统(4)或映射列
在
上具有传递性或周期点的稠密性或对初值的敏感依赖性,则相应地称系统(1)或f在
上具有传递性或周期点的稠密性或对初值的敏感依赖性。特别地,如果系统(4)或
在
上是Devaney混沌的,则称系统(1)在
上是Devaney混沌的。
3. 广义符号混沌系统的构造
设
,
定义如下:对任意
和
,
(8)
其中,
是一个正整数,
是两个正整数,
是一个周期为p的周期整数数列,即对一切
,有
,以及a与q互素,且b与q互素。
不难发现,利用式(8)所定义的函数f可以生成如下的时变广义符号动力系统
,
,
(9)
显然,系统(9)是系统(1)的特殊情形,因而它会等价于如下的一个无穷维离散系统:
,
,
(10)
其中,
和
是由f所导出的一个映射,
,且对任意
,都有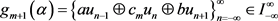 ,
。
,
。
引理1. 式(10)所定义的
是周期为p的一列映射,即
,
。
事实上,由已知条件和式(9)和(10),对任一
和任意
,有
。
推论1. 设
是由系统(10)的一列系统映射,则对一切
,都有
(11)
利用自然数性质,容易证明如下结果。
引理2. 对任一正整数m和
,存在
,使得
和
。
定理1. 系统(9)在度量空间
上是Devaney混沌的,其中,度量
由式(7)定义。
证明:由定义4,只需要证明系统(10)是
上的Devaney混沌系统。
首先,将证明系统(10)在
上具有传递性。
设U和V是
中任意两个非空开子集,则对任一
和
,存在常数
,使得
和
。因此,由式(7)可知,存在一个正整数M,使得
(12)
对任一
,记
,
其中,
,且
,
。
一般地,利用递推法,对任意
和
,都有
,
,
其中,
由式(6)定义,且
(13)
以及
和
是由式(8)定义的函数f唯一决定的两个函数,
。
由引理2可知,对任一给定的
和整数
,都存在整数
,使得
,
(14)
对于
和
,由式(12),(13)和(14),存在
,满足
,对
,且依次选取
和
满足
,
,
,
。
因此,
,且
。于是,系统(10)在
上是传递的。
其次,将证明系统(10)在
上具有稠密的周期点集。
对任一
和
的任意邻域U,都存在正数
和某个充分大整数
,使得
和
(15)
类似于上面传递性证明,一定存在
,使得
,
,
,
。
因此,
和
。
由式(11),可得
。利用归纳法可证:对任意
,都有
。因此, 和
是系统(10)或映射列
的一个周期点。于是,系统(10)在
上具有周期点的稠密性。
和
是系统(10)或映射列
的一个周期点。于是,系统(10)在
上具有周期点的稠密性。
最后,将证明系统(10)在
上具有对初值的敏感依赖性。
设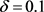 ,
,且U是
的任一邻域,则存在
和充分大整数
,使得
和式(15)成立。因此,类似于上面证明,存在
,使得
,对任意
,且依次选取任一
,存在
,使得
,以及
,
,且U是
的任一邻域,则存在
和充分大整数
,使得
和式(15)成立。因此,类似于上面证明,存在
,使得
,对任意
,且依次选取任一
,存在
,使得
,以及
,
。
于是,
和
。
因此,系统(10)在
上具有对初值的敏感依赖性。
综合上面的证明过程可知,系统(10)在度量空间
上是Devaney混沌的。证毕。
例1. 考虑如下时变离散时空系统
(16)
其中,
和
,对任意
,
表示模2加法运算。
由于系统(16)是时变广义双边符号系统,因此,现有的判断标准无法判断系统(16)是否是Devaney混沌的。但是,由于
都是周期数列,因而系统(16)是系统(9)的特殊情形,且满足定理1中的各项条件。因此,由定理1,系统(16)在度量空间
上是Devaney混沌的。
下面来分析系统(16)解的伪随机性能,并利用它来构造一种序列密码算法。
首先,考虑到系统(16)是Devaney混沌的,其解理论上应该是混乱和接近不相关的。下面对系统(16)解序列的混乱性和相关性进行数值计算,并与Logistic系统产生的混沌序列的混乱性和相关性作对比,可见图1,其中(a)和(b)分别为上述符号系统和Logistic系统的解的混乱性,(c)和(d)分别为上述符号系统和Logistic系统的解的相关性。直观上看,符号系统在三维空间中的混乱性比Logistic所在二维空间中的混乱性要更“乱”,且它们的相关性几乎相同。因此,仿真说明本文所研究的符号系统的解序列具有很好的类随机性。
其次,考虑文献 [9] 曾给出了多种序列随机性能的检测方法,下面再来对上述符号系统解序列进行其中的3种最常见随机性检测,即单比特、扑克和游程检验,其中,单比特检测主要用于序列中0和1的均匀分布性检测,扑克检测用于序列的多个连续比特的均匀分布性检测,游程检测用于游程总数的随机性检测。这些都能从某个方面分析序列的随机性能的好坏,其检测仿真效果见表1。
最后,再利用系统(16)的解
中的数值构造如下的一种流密码系统:

Figure 1. Solution confusion and correlation
图1. 解的混乱性与相关性

Table 1. Three common random number detection results
表1. 三种常见随机数检测结果图
1) 选择一副数字灰度图像作为明文,利用Matlab语言将该图像表示为数字矩阵
,其中,每个明文数值
;
2) 先选取一个JK序列,以它作为初始值,再利用系统(16)的某个解
来产生密钥流序列,并将该二元密钥流序列转化为值为0~255的序列;
3) 加密变换:
,其中,
表示密文数值,
表示逐比特异或运算;
4) 解密变换:
。
将上述简单加密算法与基于常见的Logistic系统加密算法进行对比,它们的Matlab仿真效果可参见图2。
直观上,由图2可以看出,两种算法都能进行正确的加解密。而且,再对图2中两种算法加密效果图的3种方向的相关性进行仿真计算,计算结果可见表2。

Table 2. Correlation coefficient between original image and encrypted image
表2. 原始图像和加密图像的相关系数
从表2中,可以看出,原始图像在各个方向的相关系数都接近1,而加密图像各个方向的相关系数则都在0左右。而且,利用本文符号系统加密的效果比利用Logistic系统加密的效果略有改善。这说明本文符号加密系统更有利于有效抵御统计攻击。
4. 小结
本文研究了时变双边广义符号系统的混沌类随机性,并对该系统所产生的序列进行了多种伪随机性能分析,分析说明系统解序列的伪随机性能优良。在此基础上,构造了一种序列密码算法,仿真实验说明了该算法在数字图像加密中具有良好的效果。本文的研究在混沌序列密码算法研究领域具有一定的指导意义。