基于PLC的非线性水箱的预测控制研究

Research on Predictive Control of Nonlinear Water Tank Based on PLC

摘要: 工业生产过程往往是一个大惯性、大迟延、非线性的控制对象，常规的PID控制很难达到良好的控制效果；预测控制的提出，可以有效地解决非线性、大迟延、大惯性的问题。本文选取典型的工业过程对象即非线性水箱进行预测控制的研究。在进行水箱试验前，需要在MATLAB上进行对象模型的辨识，以及必要参数的预整定。经实验结果表明，有约束预测控制算法在控制品质和调节时间上是优于传统的PID控制的，且该算法的鲁棒性能良好。

Abstract: The industrial production process is often a large inertia, large delay, and nonlinear control object. It is difficult to achieve good control effect by conventional PID control. The prediction control can effectively solve the problems of nonlinearity, large delay and large inertia. This paper selects the typical industrial process object, namely the nonlinear water tank for predictive control research. Before the tank test, it is necessary to identify the object model and pre-define the necessary pa-rameters on MATLAB. The experimental results show that the constrained predictive control al-gorithm is superior to the traditional PID control in terms of control quality and adjustment time, and the robust performance of the algorithm is good.

1. 引言

随着人们对工业生产过程的控制要求越来越高，工程师们除了在系统辨识、鲁棒控制、自适应控制、模型简化等方面寻求突破外，还开始尝试寻找一些新的控制思路。因此，预测控制并不是从某种理论衍生推导出的产物，而是直接来源于工业生产实践 [1] [2] 。

本文首先对物理实验平台的非线性水箱进行了分析和实验，获得了流量——水位的飞升曲线，并在MATLAB上进行了辨识，获取了不同水位工作点下对象模型参数；考虑PLC控制器存储空间有限等问题对预测控制算法编程进行了优化，A3030型艾默生的非线性水箱这种典型的工业过程模型作为控制对象。设计了PLC实现非线性水箱水位预测控制系统；通过预测控制与PID的对比试验研究，从调节时间快慢，超调量，鲁棒性等方面验证了预测控制对非线性水箱控制的可实现性和优越性。

2. 动态矩阵控制(DMC)

2.1. 基本原理介绍

动态矩阵控制(DMC)是一种基于阶跃响应的，并采用控制增量的算法。DMC的优越之处在于控制中加有积分环节，可以有效地消除系统的静态误差 [3] 。

DMC算法包含三个部分：预测模型、滚动优化、反馈校正 [4] 。其算法流程图如图1所示。

2.2. 基于黄金分割法的有约束预测控制器设计

在实际的工业控制过程中，执行器的输出都是带有约束的，即输出范围只能在0%~100%之间，因此，在工业环境下设计控制器时，考虑输出约束后，动态矩阵控制简化算法的控制增量就会发生变化。本文采用黄金分割法设计有约束的预测控制器， $\Delta u\left(k\right)$ 的最优值计算将在有约束的条件下进行。

2.2.1. 黄金分割算法介绍

黄金分割算法是一种非常适合求解一维函数在 $\left[a,b\right]$ 区间内的极值问题的经典算法。其主要的求解思想是沿着某一个已知的方向，通过“优胜劣汰”的原则逐步地缩小搜索区间，然后逐步逼近优化问题的最优值 [5] 。

黄金分割法具体的计算步骤为：

(1) 确定收敛精度 $\epsilon$ ；

(2) 从 $\left[a,b\right]$ 区间内选择 $r_1,r_2\left(r_1<r_2\right)$ 两点，然后将 $\left[a,b\right]$ 分成三段；

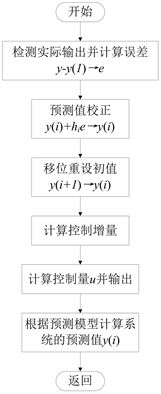
Figure 1. Flow chart of unconstrained dynamic matrix control algorithm

图1. 无约束动态矩阵控制算法流程图

(3) 判断 $f\left(r_1\right)$ 和 $f\left(r_2\right)$ 的大小，若 $f\left(r_1\right)>f\left(r_2\right)$ ，则收敛区间则需要更新：

$a=r_1$

$r_1=r_2$

$r_2=a+0.618\times \left(b-a\right)$

若 $f\left(r_1\right)>f\left(r_2\right)$ ，则收敛区间的更新公式为：

$b=r_2$

$r_2=r_1$

$r_1=a+0.382\times \left(b-a\right)$

(4) 若 $\frac{b-a}{a}<\epsilon$ 则停止迭代，极值点为 $\frac{a+b}{2}$ ，函数的极值为 $f\left(\frac{a+b}{2}\right)$ ；否则，返回步骤(3)继续迭代。

2.2.2. 基于黄金分割法的有约束预测控制器设计

设计有约束的控制器时，选取约束目标函数为 [6] [7] [8] ：

$\min J\left(k\right)={\Vert w_p\left(k\right)-{\tilde{y}}_{p0}\left(k\right)-A_2\Delta u\left(k\right)\Vert }_Q^2+H^{T}RH\Delta u^2(\; k\; )$

在线求解 $\Delta u\left(k\right)$ 最优值的问题定义式为：

$\begin{array}{l}\Delta u\left(k\right)=\arg \min J\left(\Delta u\left(k\right)\right)\\ s.t.\Delta u\left(k+i\right)\in \left[\Delta u_{\min },\Delta u_{\max }\right],\Delta u_{\min }<0,\Delta u_{\max }>0\\ u\left(k+i\right)\in \left[u_{\min },u_{\max }\right],u_{\min }\ge 0,\Delta u_{\max }>0\\ \Delta u\left(k+i\right)={\gamma }^i\Delta u\left(k\right),1\le i\le M-1\end{array}$

由上述公式作简单的推导可以得到如下的关系：

$\begin{array}{l}u\left(k\right)=\Delta u\left(k\right)+u\left(k-1\right)\\ u\left(k+1\right)=\gamma \Delta u\left(k\right)+\Delta u\left(k\right)+u\left(k-1\right)\\ u\left(k+M-1\right)=R_i\Delta u\left(k\right)+u\left(k-1\right)\end{array}$

其中， $R_i={\displaystyle \sum {\gamma }^i}$

结合上述 $\Delta u\left(k\right)$ 的两个约束条件，通过推导，可以得到最终的约束范围是：

$\Delta u\left(k\right)\in \left\{\begin{array}{c}\left[\max \left(\Delta u_{\min },\frac{u_{\min }-u\left(k-1\right)}{R_{M-1}}\right),\min x\left(\Delta u_{\max },\frac{u_{\max }-u\left(k-1\right)}{R_{M-1}}\right)\right],\gamma <1\\ \left[\max \left(\frac{\Delta u_{\min }}{{\gamma }^{M-1}},\frac{u_{\min }-u\left(k-1\right)}{R_{M-1}}\right),\min x\left(\frac{\Delta u_{\max }}{{\gamma }^{M-1}},\frac{u_{\max }-u\left(k-1\right)}{R_{M-1}}\right)\right],\gamma \ge 1\end{array}\right\}$

根据上述得到的 $\Delta u\left(k\right)$ 的约束范围，即可在设定的 $\left[a_1\left(t\right),b_1\left(t\right)\right]$ 区间内进行最优值搜索求解。则基于黄金分割法和集结优化的有约束预测控制算法流程图如图2所示。

3. MATLAB仿真实例

3.1. 控制对象的辨识及参数的获取

以实验室的A3030型艾默生的非线性水箱为控制对象，通过调节控制阀，观察水位的变化情况，当水位趋于稳定不在发生变化时，此时可以通过系统自带的数据采集工具，截取实时趋势曲线中，变化较

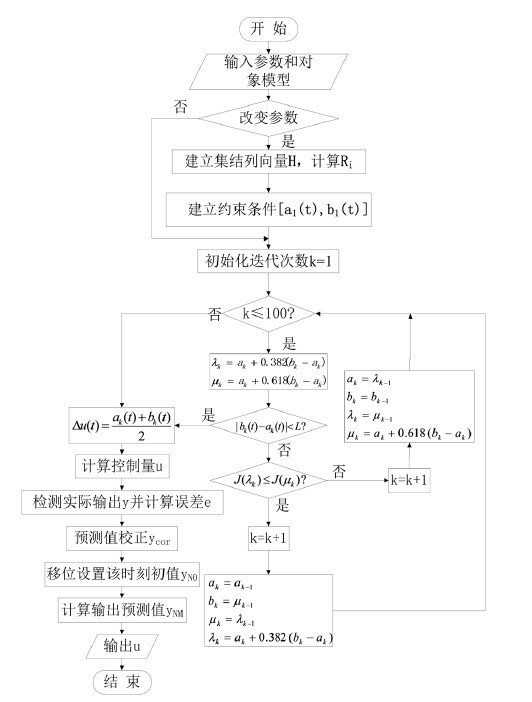
Figure 2. Flow chart of constrained predictive control algorithm based on golden section method

图2. 基于黄金分割法的有约束预测控制算法流程图

为明显的一段。图3为水箱在阀门扰动下得到的飞升曲线，图3中，经过去坏点、初始值归零化等处理后，通过热工遗传算法辨识可以得到该水箱的传递函数为：

$G_{\left(s\right)}=\frac{3.7766}{{\left(52.676s+1\right)}^2}$

3.2. DMC算法和PID算法的比较

在MATLAB平台上对已知的被控对象进行常规的PID优化和DMC优化。

运用DMC算法对该模型进行优化，选取参数如下：

模型时域： $N=200$

预测时域： $P=200$

控制时域：

选取： $\gamma =0.5$

设定区间 $u\in \left[-6,6\right];\Delta u\in \left[-16,16\right]$

由图4可知，① 号曲线为DMC算法优化后的曲线；② 号曲线为PID算法整定后的曲线。通过曲线的对比，可以得到DMC算法对被控对象的调节效果和品质远高于常规的PID控制，集中体现在DMC算法无超调，且调节时间远快于PID算法，所以，可以得出，DMC算法在控制策略和控制品质上是优于PID控制的。

Figure 3. Flying curve of nonlinear water tank under valve disturbance

图3. 阀门扰动下非线性水箱的飞升曲线

Figure 4. Simulation results

图4. 仿真结果

4. 基于PLC的水箱控制试验

4.1. 实验设备介绍

A3030型艾默生过程自动化实训系统通过实际流体(自来水)的流量控制和液位控制来模拟对实际对象的控制和设备管理，它充分展示了DCS分散控制功能，体现了控制系统和现场仪表间的协同运作能力以及在PID回路之外建立设备管理平台为用户带来预诊断功能的先进理念，由于上水箱是一个圆筒状模型，一个具有典型非线性特征的对象，可以模拟很多实际工业过程被控对象。

现场设备包括：压力变送器、温度变送器、流量变送器、分析仪表，无线振动变送器，阀门、阀门定位器等。实验室项目融合了当前先进的各类通讯模式：HART、FF (基金会现场总线)以及Wireless Hart 智能无线通讯协议。被控对象的实物图如图5。

4.2. 实验流程及实例

OVATION是美国开发的新型分散控制系统，它既包含过程控制技术，又吸收了企业管理信息技术，系统在硬件上采用了速度快、容量大的设备，保证系统的高性能运行；通讯网络使用标准的以太网，可靠性高、速度快、开放性高，提升其多任务、多数据的工作能力。

本次实验以单容水箱为被控对象。通过第二章的黄金分割算法的计算，可以得到的所需的模型参数 $a\left[i\right]\left(i=1\cdots N\right)$ 和控制器增量系数 $dt$ 。将PLC中的程序初始化后赋值。然后将PLC与DCS立柜进行通讯连接，在Ovation系统上进行必要的通信点的配置和逻辑图的搭建。水箱水位的控制趋势图可以通过自带软件获取。本次实验总体流程如图6。

图7中A曲线为水位变化趋势，B曲线为控制器变化趋势。实验截取了其中10分钟的水位趋势变化图，可以看出①时刻水位能够在极短的时间内稳定下来；在稳定后的5分钟也就是②时刻通过改变出水口的插槽，从而改变对象的模型，来观察该算法的鲁棒性。通过实验可以看出，DMC算法确实能够提高系统的控制品质，集中体现在调节时间加快，超调量低，还可以看出该算法的鲁棒性良好。

无论是从第二节的仿真研究还是第三节的实验来看，通过对比可以看出：针对大迟延、大惯性、非线性的对象，从控制的品质来讲，都是DMC算法优于PID控制策略，集中体现在系统的调节时间加快、超调量降低、鲁棒性增强。

Figure 5. A3030 process system physics experiment platform

图5. A3030工艺流程系统物理实验平台

Figure 6. Experimental flow diagram

图6. 实验流程图

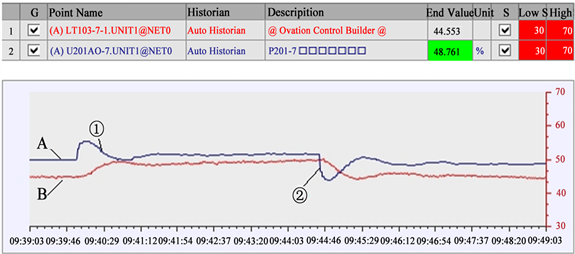
Figure 7. Water tank level control trend

图7. 水箱水位控制趋势图

5. 结论

本文首先系统分析了预测控制中DMC算法的主要过程，并提出了一种基于黄金分割算法的有约束的预测控制器设计；其次对A3030工艺流程设备进行了简要的介绍。主要完成了在MATLAB平台上对DMC算法和PID算法进行调试，通过对被控对象的调节，可以看出，所选的DMC算法在控制品质上是优于传统的PID算法。为了进一步实现DMC算法，我们将利用PLC和A3030的非线性水箱上模拟控制大迟延系统的物理实验。通过试验可以验证出DMC算法确实可以提高系统的控制品质，且该算法的鲁棒性也较好。有比较深远的意义和推广价值，未来应更进一步革新和改善DMC算法，以达到更优的品质。