基于模块化仿真的船舶动力系统任务可靠性研究

Research on Mission Reliability of Marine Propulsive System Based on Modular Simulation

摘要: 针对传统基于统计学的统计评估模型和基于可靠性框图的解释计算模型在研究多阶段复杂可修系统可靠性方面存在的数据获取困难、过程描述能力不足等问题，用面向对象的模块化仿真方法，将动力系统的任务过程按任务目标分解为若干子过程；然后，通过对各子过程内部运行规则的仿真建模和子过程之间变迁规则的描述，建立多任务过程、多使用状态的复杂可修船舶动力系统任务可靠性仿真模型，并将装备性能退化的影响融入到任务过程仿真中；最后，以某型船用蒸汽动力系统为例，验证了方法的可行性。

Abstract: When we study the reliability research of multistage complex repairable system, the traditional statistical evaluation model based on statistics has data acquisition problems and the interpreta-tion calculation model based on reliability block diagram has process description problems. An object-oriented modular simulation method was used to decompose the task process into several sub-processes according to the task target. And then, through the modeling of internal running rules of each sub-process and the description of the change rules between sub-processes, a mission reliability simulation model of a complex repairable ship power system with multi task process and multi use state was established, and the effect of gradual failures were also integrated into the simulation of the task process. Finally, a certain type of marine steam power system was taken as an example to verify the feasibility of this method.

1. 引言

船舶动力系统是典型的可修系统 [1] [2] ，其可靠性研究属于多阶段复杂可修系统的可靠性研究范畴。目前，对于复杂可修系统的可靠性分析，在许多情况下为了简化问题，往往忽略系统使用中的维修过程或者简化系统本身的使用过程，导致分析对象与实际产生较大的误差。传统的统计学和解释计算方法在进行船舶动力系统不同任务过程的可靠性评估时，存在一些难以逾越的困难，具体如下：

统计学方法是采用一定的统计评估模型，通过统计一段时间内系统任务执行情况的统计，计算出动力系统的任务成功率 [3] [4] 。统计方法的最大缺点是需要大量统计数据，而动力系统在不同阶段执行的任务类型通常是不相同的(例如：持续时间、维修保障、装备工作时间等)，要获得大量相同情形下动力系统的统计数据比较困难；即便能够获得部分相同或者类似情形下动力系统的运行数据，并统计得到动力系统的任务成功率，也无法完全排除其中一些不可预见因素(例如：备品备件的库存量和完好性、维修人员水平、维修设备状态等)对评估结果的影响。解释计算方法是建立系统的可靠性框图，并在此基础上分析得到系统的解释计算模型 [5] [6] 。但是，对于船舶动力系统这类复杂可修系统而言，当系统的使用过程与维修过程在时间和空间上相互交叠时，如果不进行大范围的简化，建立其解析模型是很难的 [7] [8] ；此外，船舶的任务过程通常包含多种任务阶段，评价各任务阶段成功与否和完成程度的指标往往不相同 [9] [10] ，因此在解释计算时建立的动力系统可靠性框图必须是动态的。目前，常用的复杂可修系统解释计算方法主要有马尔科夫和半马尔科夫分析 [11] [12] 等。这两种方法的状态分析过程比较复杂，而且描述复杂系统动态使用和维修过程的能力有限，很难准确绘制出船舶动力系统任务过程的动态可靠性框图。

综上所述，对于船舶动力系统的任务可靠性研究，传统的统计学方法在统计数据获取上有困难，而解释计算方法在过程描述能力上存在不足。本文采用面向对象的模块化仿真方法 [13] ，对船舶动力系统的任务过程进行分析，按任务目标将动力系统的任务过程分解为若干有不同使用要求和评价指标的子过程，然后分别对各子过程开展可靠性研究，最后进行数据综合，计算得到整个任务过程的可靠性。在上述过程中，对子过程变迁规则的描述是关键，依据子过程的变迁规则调度对象模型来模拟任务过程的复杂性，通过重复多次的仿真来覆盖事件发展的多样性，就能够较好地克服统计学和解释计算方法在统计数据获取和过程描述能力上遇到的困难。

2. 仿真分析框架

仿真系统分为对象设置和统计分析两大模块，如图1所示。由于船舶动力系统的任务成功率主要受船舶任务、装备系统和维修保障三方面因素影响，所以对象设置模块包括任务设置、装备系统设置和保障力量设置三个子模块。仿真系统除了输出任务成功率外，还希望能够分析影响任务成功的因素以及维修保障配置的合理性，所以统计分析模块包括维修延误统计、备件消耗统计和资源满足统计三个子模块。

在船舶的实际任务过程当中，主要包括装备故障、故障维修和备件筹供三方面的事件，这些事件是依附船舶任务产生的，所以仿真模型相应分为船舶使用仿真模块、故障维修过程仿真模块、保障资源筹供仿真模块和系统调度模块四部分，其相互关系和运行方式如图2所示。

3. 系统建模

3.1. 船舶任务模型

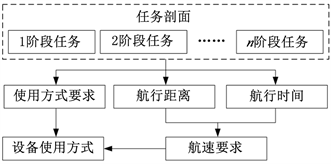
动力系统在不同使用方式下，其能达到的最高航速是不同的，所以不同使用方式对应不同的航速极限。一般情况下，仿真中的航速极限由以下方式确定：在动力系统能够满足任务要求时，视情况提前20%的时间余量航行；在动力系统满足不了要求时，按动力系统所能达到的最大航速航行。

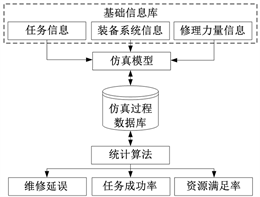
Figure 1. Simulation framework of mission reliability of marine propulsive system

图1. 船舶动力系统任务可靠性仿真框架

Figure 2. Schematic diagram and running method of mission reliability simulation model of marine propulsive system

图2. 船舶动力系统任务可靠性的仿真模型组成及运行方式

此外，出于船舶安全等其它因素的影响，船舶在执行任务过程中不仅有航速要求，对动力设备还有使用方式上的要求，只有当两者同时满足时，船舶任务才能顺利完成，计算流程如图3(a)所示。

3.2. 维修系统模型

船舶在执行任务过程中发生故障后，可依靠船员和随船携带的维修设备、备品备件等修复装备，提高船舶的任务成功率。维修系统类似于排队系统，故障装备形成等待维修队列，但是维修不同装备所需的维修资源是不同的，只有当所有维修资源都满足要求时才能进行维修，否则继续等待，计算流程如图3(b)所示。

3.3. 装备系统模型

船舶动力系统组成复杂而且通常设计有冗余装备，使得在相同任务要求下有多种使用方案，难以直接画出可靠性框图。本文采用面向对象的仿真方法建立装备系统的多层次仿真模型，从船舶任务到具体装备按层次确定动力系统运行方式，进而确定需要投入使用的装备种类和数量，计算流程如图3(c)所示。

(a) 船舶任务模型 (b) 维修系统模型 (c) 装备系统模型

Figure 3. Model flow chart of mission reliability of marine propulsive system

图3. 船舶动力系统任务可靠性模型计算流程图

4. 可靠性分析流程

仿真采用最近下次事件原理的变步长推进，选择各未来事件中距仿真指针最近的时间为仿真步长，如图4所示。

在仿真开始时，首先产生一批故障事件，以故障时间最小者为最先发生的故障，将仿真指针推进到该故障对应的时刻；然后，开始故障维修并随机抽样一个修复时间，故障时间与修复时间之和即为该故障的故障修复时间。由于在故障维修过程中，其他独立设备仍在继续工作，因此下一个状态转移时刻就是该故障修复时刻与其他故障发生时刻集合中的最小者。由上述仿真过程可见，这种采用最近下次事件原理的变步长仿真方法能够跨越系统的不变状态点，与传统定步长仿真方法相比，计算效率更高。

4.1. 检查状态转移

当时间大于等于最小到达时间时，表示该事件正式发生，系统调度模块根据条件触发故障维修过程仿真模块、保障资源筹供仿真模块或船舶使用仿真模块，产生相应的事件，各模块的工作流程如图5所示。

4.2. 产生下一批次事件到达时间

当状态转移后，被触发的仿真模块重新安排工作，产生其余仿真模块状态不变前提下的事件序列，得到本模块下一批次事件的到达时间。

4.3. 工作和预测调整

由于装备的故障维修、保障资源筹供和使用过程彼此影响，所以故障维修过程仿真模块、保障资源筹供仿真模块和装备使用仿真模块的每一次状态转移会对其它模块造成影响，其规则如下。

1) 当一批维修保障资源到达后，故障维修过程仿真模块根据新资源安排修理工作，并根据重新安排的修理工作开始修理时间和保障资源计算；如果修理工作消耗的保障资源超过库存则计算保障资源的补充量，保障资源筹供仿真模块根据新的补充需求产生补充时间并把最小补充时间提交给系统调度模块。

2) 当修理工作完成后，触发船舶使用仿真模块，使用模块判断是否改变系统的工作状态并预测最小故障时间；同时故障维修过程仿真模块检查修理队列并重新安排修理工作，并计算修理时间；修理工作可能导致维修保障资源消耗，所以须检查库存，根据存储策略判断是否触发保障资源筹供仿真模块。

3) 当故障发生时，直接触发船舶使用仿真模块，重新调整系统工作状态，流程与(2)相同。

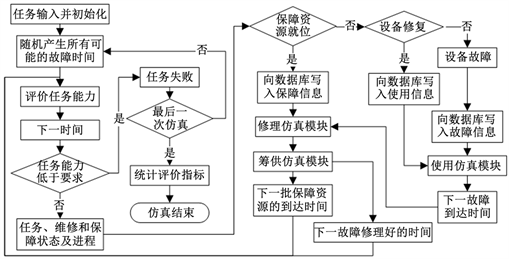
Figure 4. Flow chart of mission reliability simulation

图4. 任务可靠性仿真流程图

(a) 船舶使用仿真模块 (b) 保障资源筹供仿真模块(c) 故障维修过程仿真模块

Figure 5. Simulation flow of every module

图5. 各模块工作流程图

上述三个事件的触发判断以及三个仿真模块之间的数据交互都通过数据库读取来完成，所有仿真模块运行产生的数据也存储在数据库中。

5. 案例研究

5.1. 任务描述

假设某型蒸汽动力船舶的当前任务为：在80小时内航渡1500海里到达预定海域，然后锚泊待命，随时准备进行海上500海里内的机动巡逻，最后进入5小时的全速航行状态，任务完成后航行2000海里返回，全过程无补给。

5.2. 最大航速及油耗

从任务要求可见，各任务阶段除了运行装备的要求外，还有完成时间的限制，所以航速与任务成功与否直接相关。此外，由于在整个任务过程中没有燃油补充，所以油耗也是需要考虑的因素。该型船用蒸汽动力系统在正常使用情况下，不同航速下的功率与燃油消耗率关系如表1所示。表1中，F为该型船用蒸汽动力系统在100%工况下的小时燃油消耗量，取为总载油量的3.08%。

在正常使用方式下，船舶航速与动力系统功率直接的关系如式(1)所示 [14] 。

(1)

由式(1)可得，锅炉最大上水量下降和动力系统系统效率下降后能达到的最大航速如式(2)所示。

$V=V_0\sqrt[3]{Q_f/Q_{f0}}$ ， $V=V_0\sqrt[3]{\eta /{\eta }_0}$ (2)

式中：V₀为最大航速，V为实际航速；N₀为系统最大功率，N为实际功率；η₀为系统在最大航速下的效率，η为实际效率；Q_f0为系统在最大航速下的产汽量；Q_f为实际产汽量。

5.3. 任务可靠性仿真结果

对于动力系统而言，任务成功的标准为所有任务阶段都能够顺利完成。故障类型和维修保障资源配置等都会影响动力系统的修理频率和维修时间，进而影响动力系统的任务可靠性；而且不同故障率或不同维修保障资源，对任务成功率的影响是不同的。假设该型动力系统的故障都是可修故障，故障间隔时间为3000小时，平均维修时间满足正态分布(μ = 9 h, σ = 1.2)，维修资源充足。在不考虑动力设备性能退化因素时，进行1000次仿真，结果如表2所示。

5.4. 装备性能退化的影响分析

整个动力系统从投入使用后就不断产生各种性能退化，靠不间断的维修保养，系统的性能才得以保持，因此在安排船舶任务时，应统筹考虑系统当前的技术状态。本节中以锅炉上水量下降和动力系统效率下降为例讨论装备性能退化对动力系统任务可靠性的影响。

1) 锅炉上水量下降

最大上水量下降时，对应于不同的任务要求的1000次可靠性仿真结果如表3所示。

表3中：Q_fmax为故障后能到达的最大给水量。

由表3可见，当任务时间比较充裕时，船舶完成航渡任务的概率基本不受最大上水量的影响。当完成时间要求比较紧迫时，一旦在任务过程中因故障造成延误，船舶在剩下的时间里，动力系统有一定概率因为达不到阶段任务所需要的航速而失败。同时，由于任务时间短，任务过程中需长时间维持较高的航速，高航速下的耗油量相对较高，可能造成返航阶段因燃油耗尽而失败的概率增加。

2) 系统效率下降

不考虑船体因素影响时，蒸汽动力系统的效率下降主要由两方面原因引起：一是锅炉传热系数下降，二是系统耗汽量增加。在不同锅炉传热系数和系统耗汽量的影响下，不同任务阶段成功率的1000次可靠性仿真结果如表4所示，其中k_t0为没有性能退化情况下的锅炉传热系数，k_t为退化后的锅炉传热系数。

可表4见，系统效率下降导致任务成功率下降的主要原因是最大航速下降和燃油消耗率增加，前者会导致按时到达的概率下降，后者导致任务失败的概率增加。

Table 1. Relationship of power and fuel consumption rate under different speed

表1. 不同航速下动力系统功率与燃油消耗率的关系

Table 2. Probability of success under mission phases

表2. 船舶在各任务阶段的成功率

Table 3. Probability of success in Navigation and return phase under different required time and feed water

表3. 最大上水量和时间要求下的航渡阶段(Pn)及返航阶段(Pr)的成功率

Table 4. Probability of success in Navigation starts and return phase under different required time and efficiency

表4. 系统效率和时间要求下的航渡阶段(Pn)、启动阶段(Pq)及返航阶段(Pr)的成功率

6. 结束语

本文根据船舶动力系统的实际使用情况，改进了以往可靠性研究中，单纯基于系统部件间逻辑关系的可靠性研究方法，建立了多任务过程的、复杂可修的、多使用状态的船舶动力系统任务可靠性仿真模型，使得任务可靠性研究更贴近实际；以某型船用蒸汽动力系统为例进行了数字仿真，分析研究了船舶任务过程中的动态可靠性指标及其影响因素；并将装备性能退化对动力系统的影响融入到任务过程仿真中，获得了其影响方式和影响程度。研究成果不仅适用于船舶动力系统的任务可靠性分析，而且在航空航天、坦克雷达、空间飞行器等领域同样有一定的参考价值。

基金项目

国家自然科学基金面上项目(51179196)。