1. 引言
为了解决水资源时空分布不均造成的水资源短缺问题,在遵循合理性、高效性和可持续性等原则的前提下开展水资源优化配置研究,既是需水管理的核心之一,也是区域水资源系统可持续发展的关键 [1] 。国内自上世纪60年代开始水资源配置研究,经过近六十年的发展,在水资源配置理论及应用研究等方面取得了可喜的成果 [2] [3] 。近几年,针对水资源优化配置的研究进一步深入。刘德地等 [4] 通过耦合水文模型和水资源优化配置模型,定量分析了气候变化和人类活动对水资源时空分布及其配置的影响。邓铭江 [5] 通过对西北调水方案的初步分析,提出了西北“水三线”建设的空间格局与水资源配置方略。李建勋等 [6] 基于复杂性理论建立了水资源配置框架体系,并综合采用WebService、知识可视化和组件化技术进行实现以辅助配水决策。吴丹等 [7] 构建了流域初始二维水权耦合配置模型,并提出基于满意度的主从递阶交互式迭代算法对模型进行求解。张妍等 [8] 在充分考虑地表径流随机性的基础上,分别构建具有不同目标的灌区水资源优化配置模型,并应用于黑河中游灌区的水资源配置。此外,针对多目标优化求解时容易出现维数灾或陷入局部最优等问题,很多学者也是尝试改进或引入新的算法,如混沌算法 [9] 、模拟退火遗传算法 [10] 、改进的类电磁学算法 [11] 、改进的鲸鱼算法 [12] 以及蝙蝠算法 [13] 等,极大地提高了求解效率。刘德地等 [14] 从最严格水资源管理的考核要求出发,分析了目前水资源优化配置研究面临的技术问题与挑战,并针对动态的水资源优化配置模型结构、求解算法和方案评价等方面提出了对策和建议。田晶等 [15] 以社会、经济和生态效益为目标,构建了汉江中下游地区水资源多目标优化配置模型,并应用第二代非支配排序遗传算法(NSGA-II)对模型进行求解。
随着经济社会的快速发展以及生态文明建设的进一步强化,作为战略性经济资源和生态环境控制性要素的水资源,其合理配置需要考虑的因素日益增多,尤其当涉及到多个行政区域的用水时,特别是在经济发展阶段差别较大的南方地区,矛盾更为突出。以往的水资源优化配置模型通常以全区域缺水量最小为社会效益目标,难以保证各分区用水户利益分配的公平性。为了弥补这个缺陷,本文引入用水效益比指标,并采用三步法 [16] 求解跨区水资源优化配置模型,既简化了求解过程,也能充分考虑各用水户的用水公平性。汉江流域是长江中游最大支流,是国家水资源配置的战略水源地。由于流域内社会经济的发展,已经面临着水资源开发利用矛盾日益突出、用水量不断增加、水污染日趋严重和人类活动对水生态环境影响日益增加等问题。因此,本文以汉江中下游为研究对象,在论证水资源配置模型及方法适用性的同时,配置结果也能为汉江流域建立最严格的水资源管理制度提供技术支撑。
2. 研究方法
2.1. 水资源优化配置模型
本文所建模型在统筹考虑各用水户单元的需水、水量平衡、生态环境用水及各种约束条件的前提下,使各区域水量配置效益达到最优,其目标函数如下:
(1)
约束条件为:
(2)
(3)
其中
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
式中:Zk为第k分区在研究时段的总净经济效益,
,
和
分别为第k分区的农业、工业和生活用水净经济效益系数,
,
和
分别为第k分区t时刻的农业供水量、工业供水量和生活供水量,SWkt为第k分区t时刻的区间产水量,
为第k分区t时刻的上游来水量,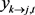 为第k分区t时刻的下游去水量,
为第k分区t时刻的河道生态需水满足系数,EDkt为第k分区t时刻的河道生态需水量,ADkt、DDkt和UDkt分别为第k分区t时刻的农业需水量、工业需水量和生活需水量。
为第k分区t时刻的下游去水量,
为第k分区t时刻的河道生态需水满足系数,EDkt为第k分区t时刻的河道生态需水量,ADkt、DDkt和UDkt分别为第k分区t时刻的农业需水量、工业需水量和生活需水量。
2.2. 多目标优化的三步法
若目标函数为单个分区的最优化,则每个分区都能求得一个可能最大效益值,但对于跨区域的水资源配置问题,面对有限的水资源,不可能使每个分区都达到最大供水效益,求解上述多目标模型比较困难。因此,本文尝试利用三步法求解,思路如下:首先建立可能最大效益模型(HWP),即以各分区的效益最大化为单目标函数,求出每个分区不同时刻的可能最大效益;其次建立最大效益比模型(HRHWP),设λ为各个分区实际效益和可能最大效益的比值,以任意时刻全区域效益比之和最大建立单目标优化模型;最后建立总效益模型(FWP),目标函数为全区域的总经济效益最大,据此即可求出最终优化配置结果。
第一步:根据分区个数n,建立n个HWP模型,以分区1为例,其目标函数如下:
(13)
式中:
为分区1在研究时段的最大可能经济效益,
,
和
分别为分区1的农业、工业和生活用水净经济效益系数,
,
和
分别为分区1在t时刻的农业供水量、工业供水量和生活供水量。
约束条件见式(2)~(12)。同理可分别求得其它分区的
。
第二步:本着用水户平等的原则,同一时刻各分区的λ应相同,据此建立HRHWP模型,其目标函数为:
(14)
约束条件:
(15)
其他约束条件同式(2)~(12)。这里的
为t时刻的效益比,
为第k分区t时刻的可能最大效益,其他符号意义同上。
第三步:基于HWP和HRHWP模型结果,建立FWP模型,其目标函数如下:
(16)
约束条件同式(2)~(12)和(15),这里的W为全区域总经济效益,其它符号意义同上。
三步法中每个模型均为单目标模型,可采用常规优化算法求解。
3. 汉江中下游水资源优化配置
3.1. 研究区概况
汉江是长江中游最大支流,发源于秦岭南麓,经汉中盆地与褒河汇合后始称汉江,于武汉市龙王庙汇入长江。干流全长1577 km (湖北省境内888 km),流域面积15.9万km2。其中,丹江口为汉江上游与中下游的分界,在汉江中下游汇入干流的主要支流有:北河、南河、小清河、唐白河、蛮河、竹皮河以及汉北河等。本次研究的对象为汉江中下游湖北省境内以汉江干流及其分支东荆河为主要水源以及补充水源的供水区域,包括武汉、襄阳、荆门、孝感、天门、仙桃、潜江等重要城市及其所辖的市、县、区以及“五三”、“沙洋”、“沉湖”等农场的全部或部分范围,面积约4.11万km2,具体见图1。
3.2. 水资源分区及水系概化
汉江流域属于长江流域的二级区,该二级区又进一步划分为三个三级区,即丹江口以上、唐白河和丹江口以下干流。本次的研究区域按水资源三级分区分别属于唐白河和丹江口以下干流区。图2为研究区水资源系统概化图。以水资源三级区套地级行政区界限,将研究区共划分为8个计算分区。其中,为了和地形GIS地图保持一致,将天门、潜江、仙桃合并为一个区域考虑。各分区面积见表1。
3.3. 模型参数
汉江流域1956~2000年多年平均地表水资源量为554.71亿m3,占长江流域地表水资源量的5.6%,相应径流深为358.3 mm,径流深低于长江流域平均值。汉江流域50%、75%和95%频率来水情况地表水资源量分别为533.44亿m3、418.71亿m3和285.02亿m3。汉江流域多年平均年地下水资源量为161.53亿m3,约占长江流域
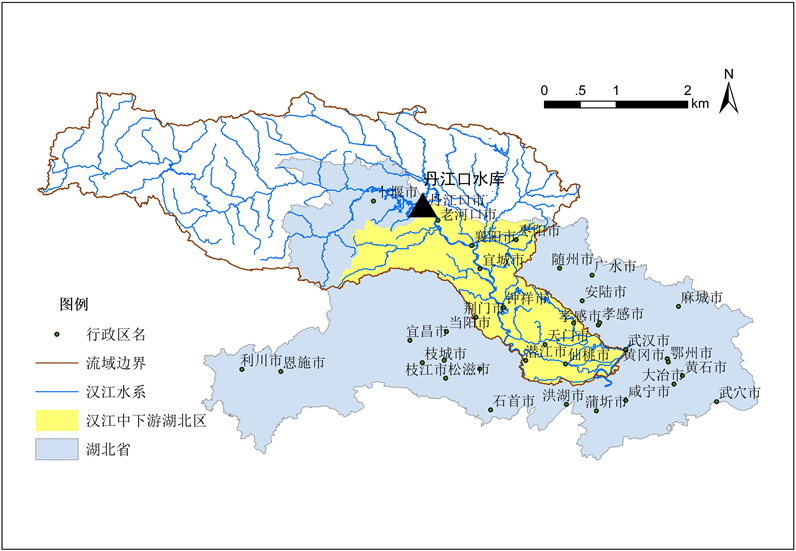
Figure 1. Sketch map of study area and location in the middle and lower Han River basin
图1. 汉江中下游研究范围位置示意图

Figure 2. Conceptual diagram for water resources system in the middle and lower Han River basin
图2. 汉江中下游研究区水资源系统概化图
地下水资源量的6%。汉江流域多年平均产水系数(水资源总量与相应降水量比值)和产水模数(单位面积水资源总量)分别为0.41和37.03万m3/km2,均低于长江流域多年平均值。
本次研究重点分析近景规划水平年2020年,并分别计算50%,75%和95%三个频率下的水资源供需关系。表2列出了研究区现状用水和规划水平年用水情况,可以看出,除神农架林区外,其他七个分区的水资源需求量增长很快,尤其是随州、襄阳、十堰和荆门市,年均增长量均在10%以上。
模型计算步长为“月”,通过输入各计算分区各用水户需水长系列、径流过程、供水工程的特性等进行供需平衡计算。根据《长江流域水资源综合规划》成果,各计算分区输入水资源量采用1956~2000年逐月长系列

Table 1. Divisions for water resources allocation in the middle and lower Han River basin
表1. 汉江中下游水资源配置模拟分区

Table 2. Comparison of water consumptions in current year and planning year in the middle and lower Han River basin
表2. 汉江中下游研究区现状与规划年需水比较
径流过程。采用水文年进行水库调节计算,其中丹江口水库常规调度图如图3所示。每个计算分区用水分四大类:生活(包括城镇生活和农村生活,其中城镇生活含河道外环境用水)、城镇工业、农业灌溉、河道内生态环境用水。城镇生活、城镇工业、农村生活年需水过程均是由年需水总量按12个月平均分配到每月。农业灌溉年需水过程是由年需水总量乘以各月灌溉分配系数得到各月需水量。河道内生态需水量采用多年平均径流量乘以最小生态流量的百分比的方法计算。唐白河区域、丹江口区域的汛期和非汛期的最小生态流量的百分比统计如表3所示。
模型中的效益系数采用效益分摊系数法确定 [17] [18] [19] 。效益分摊系数法是1996年水利部颁布的《水利建设项目经济评价规范》中指定的方法,其原理是按获取生产要素的代价比例进行贡献分摊。其中农业灌溉效益分摊系数采用试验参数法确定,其它用水活动的供水效益分摊系数采用固定资产净值(或成本)比例法确定。
农业用水净效益计算公式如下:
(17)
式中:Pa为农业用水净效益系数,元/m3;γa为农业灌溉效益分摊系数;Ai为第i种作物的种植面积,亩;Yi为有灌溉措施情况下单位面积的多年平均产量,kg/亩,可根据灌区实验室、历史资料等确定;Yoi为无灌溉措施情

Figure 3. Danjiangkou Reservoir operation chart in normal water supply operation period
图3. 丹江口水库正常运行期水库供水调度图

Table 3. Percentage of lowest ecological water demand in the rivers
表3. 河道内最小生态环境需水量占全年的百分比
况下单位面积的多年平均产量,kg/亩,可根据无灌溉措施地区的调查资料分析确定;Pi为第i种农作物产品的价格,元/kg;m为农作物种类的总数目;Ca为农业用水成本,元/m3;Wa为农业用水量,m3。
工业和生活用水净效益系数按下式计算:
(18)
式中:Pi为工业用水净效益系数,元/m3;qi为万元工业增加值用水量,m3;Ci为工业用水的供水成本,元/m3;γi为工业供水效益分摊系数。
4. 结果与讨论
4.1. 三步法求解结果及分析
HWP模型是让单个分区的效益最大化,据此求得各分区的配置水量。如模型1即代表进行水资源配置时,随州市取最大经济效益。从表4中数据分析可知,位于唐白河流域的分区,其配置效益受其它分区配水影响较大,而丹江口干流以下区域由于受到水库调蓄优化,配置效益不受其它分区的配水影响。
本次模拟步长为月,故利用HRHWP模型可求得12个月的效益比值,对每个分区而言,为了保证配水公平性,在同一月份各个分区的效益比值相同,具体结果见表5。可以看出,由于区域夏季需水量最大,实际用水满足程度相对偏低,因此其效益比值较其它季节小,而春、秋和冬季的效益比值均超过0.9。
根据FWP模型求解得到各分区的最优配置水量(表6),在50%需水频率情况下,汉江中下游湖北区域河道外的总缺水量为3.47亿m3,其中农业和工业缺水量分别为3.37亿m3和972万m3,生活用水基本满足要求。从分区来看,主要集中在唐白河流域的随州和襄阳市,其中,随州市农业缺水率高达33.1%,襄阳市农业缺水率为11.7%。
4.2. 不同频率配置结果及分析
2020规划水平年取农业灌溉需水频率分别为50%,75%和95%,采用各计算分区1956~2000年逐月长

Table 4. Optimal benefit for each division in 2020 in the middle and lower Han River basin (Unit: 0.1 billion yuan)
表4. 汉江中下游2020水平年各分区最优效益(单位:亿元)

Table 5. Benefit ratio of each month calculated by the HRHWP model
表5. HRHWP模型求得的各月效益比
系列径流过程,丹江口水库1956~2000年长系列入库径流,配合《汉江流域水量分配方案(送审稿)》中的不同水平年的各工程调水过程(含引汉济渭和引江济汉工程)进行汉江中下游湖北地区水库调节和水资源分配计算。
根据建立的水资源配置模型,对汉江流域地区的供水、用水进行了模拟计算,分析了各控制断面2020水平年不同需水频率下的供需情况,统计了各控制断面2020水平年的缺水量。由表7可知,就整个汉江中下游湖北地区而言,频率为50%、75%和95%时,研究区域的缺水率分别为3.11%、3.69%和3.94%。2020规划水平年,城镇和农村生活用水基本得到满足;而农业灌溉和河道内生态环境用水缺口较大;需水频率为50%时,农业灌溉和河道生态需水缺水率分别为5.15%和3.28%;频率为75%时,农业灌溉和河道生态需水缺水率分别为6.04%

Table 6. Optimal allocation water for each division in 2020 (50%) in the middle and lower Han River basin
表6. 汉江中下游2020年各分区最优配置水量(50%)

Table 7. Water resources supply and demand balance at different frequency in the middle and lower Han River basin
表7. 汉江中下游区域不同频率水资源供需平衡分析结果
注:农业含林牧渔畜,工业含建筑和三产,生活含河道外生态。
和3.55%;频率为95%时,农业灌溉和河道生态需水缺水率分别为6.08%和3.76%;随着频率增高,需水缺口逐步增大。由于缺少丹江口水库的调节,唐白河流域的缺水情况仍然明显较丹江口以下干流地区严重,三种频率下,总体缺水率分别达到24.84%,27.86%和29.75%。农业灌溉缺水率和河道内生态环境缺水率更是分别高达30.13%和30.04%,33.20%和32.41%,35.05%和34.00%。受丹江口水库的调蓄,丹江口以下地区总体缺水率分别为0.49%,0.57%和0.65%。各子区城镇生活、农村生活和城镇工业用水都基本上没有用水缺口。
分析各分区的水资源供需情况发现(见图4),除孝感市和武汉市不缺水外,其他区域均存在不同程度的缺水,其中以唐白河流域随州市的缺水量最大,缺水率为33.16%;其次是襄阳市,缺水率为24.51%。
5. 结论
本文为了保证跨区域各用水户的利益分配公平性,通过引入用水效益比指标,将跨区多目标水资源配置问题转化为HWP-HRHWP-FWP三阶段模型,大大简化了高维优化求解过程,并以汉江中下游区域水资源优化配置为例,验证了所提方法的适用性,主要得到以下研究结论:
1) HWP模型结果表明,位于丹江口水库以上的分区,包括随州市和襄阳市,其配置效益受其它用水分区配水影响较大,而丹江口干流以下区域由于受水库调蓄优化,配置效益不受其他分区配水影响,全区总配置效益可达2150.55亿元。
2) 从HRHWP模型结果得到的效益比看出,由于夏季需水量最大,效益比值相对较小,而春、秋和冬季的效益比均超过0.9,表明夏季用水满足程度低于其它季节。
3) FWP模型结果表明,2020水平年在50%频率下,汉江中下游湖北区域河道外的总缺水量为3.47亿m3,其中农业和工业缺水量分别为3.37亿m3和972万m3,生活用水基本满足要求。
4) 当频率分别为50%、75%和95%时,2020年汉江中下游湖北地区缺水率分别为3.11%、3.69%和3.94%。其中,城镇和农村生活用水基本得到满足,而农业灌溉和河道内生态环境用水缺口较大。随着频率增高,需水缺口逐步增大。
5) 从三级水资源分区来看,由于缺少丹江口水库的调节,唐白河流域的缺水情况明显较丹江口以下干流地区严重,三种频率下总体缺水率分别达到24.84%,27.86%和29.75%。而丹江口以下地区总体缺水率分别仅为0.49%,0.57%和0.65%。
基金项目
国家自然科学基金重点项目(51539009)资助。