1. 引言
近年来,随着油气勘探的不断深入和开发的难度加大,地震技术从构造研究逐渐深入到岩性识别和烃类检测。利用叠前弹性反演能够直接给出纵、横波速度与密度信息,在其基础上可进一步计算泊松比、拉梅常数等其他弹性参数或组合弹性参数。然而,由于影响地下岩石弹性特征的因素众多,造成参数反演具有多解性,需要利用先验信息建立岩石物理模型,从而进行定量或者定性解释,以达到储层岩性识别和烃类预测的目的 [1] [2] [3]。
岩石物理模型的构建有助于计算地下储层岩石的弹性参数,提高岩石物性参数的反演精度,进而更好地了解地下含油气储层特征及流体分布规律,在储层岩性、物性分析以及流体识别分析中发挥着重要的作用 [4] [5] [6]。岩石骨架在干燥条件下的地震弹性特征可以通过等效介质模型或者已有的岩石物理经验关系获得 [7] [8]。但由于储层岩石地震弹性性质的区域性造成等效介质模型以及经验关系并不完全适用,需要在模拟储层条件下对目标储层岩心样品进行系统的地震岩石物理试验来确定关键参数或者对已有模型的标定 [7] [8]。对于两相(气/水、油)或多相流体饱和(气/水/油)岩石,地震勘探中一般用Gassmann方程和有效流体模型来定量表征流体替换过程中地震弹性性质的变化 [9] [10]。Gassmann方程计算结果代表严格低频条件,由于储层岩石孔隙结构的不均匀性造成流体流动相关频散作用,对岩石地震弹性性质有明显影响,如储层岩石微观孔隙尺度不均匀所形成的“喷射”流作用,其特征频率可位于测井频段;同时,已有研究结果表明,在考虑孔隙分布的情况下速度频散曲线并无明显的低频段,即地震频段(<100 Hz)或者测井频段(10~20 kHz)并不完全等同于低频条件,造成在构建岩石物理模型时仅用Gassmann方程表征孔隙流体影响从而定量解释地震或者测井结果,会出现明显预测误差 [11] [12] [13] [14] [15]。
近几年,新疆车排子地区春光油田在沙湾组、古近系、白垩系等多层系不同砂岩体系中陆续发现和开采了一批大小不等、与岩性有关的油藏,展示了巨大的勘探潜力。沙湾组中-高孔隙度砂岩为研究区主要勘探层位,但砂体规模通常较小,油层薄且单一,储层横向物性变化快,是典型的复杂岩性油藏。有学者通过储层岩性物理特征分析,利用地震正演分析技术,验证油砂体的类亮点地震反射特征,总结出了一套以“亮点”技术为主的储层预测方法;应用实际测井资料进行地震正演、流体替换和AVO模拟,发现沙湾组砂岩在不同含油饱和度时具有不同的AVO响应特征 [11] [12] [13] [14] [15]。但由于对春光油田沙湾组储层砂岩岩石物理特征缺乏系统性、规律性认识,影响到振幅分析、波阻抗反演等储层预测方法的适用性和应用效果,使得储层及油层的分布情况难以进行更为准确的地震预测。
笔者以春光油田沙湾组砂岩岩心样品测试结果为基础,利用Mori-Tanaka非接触模型,从微细观力学角度综合考虑储层砂岩孔隙度、孔隙形状及微裂隙(在相同有效压力下容易被压缩,主要表现为颗粒基础边界和微裂隙)含量对干燥岩石骨架弹性性质的影响;结合试验结果对模型参数进行标定,进而建立表征目标储层岩石骨架地震弹性性质的岩石物理模型。在该基础上,再利用孔隙尺度喷射流作用模型替代传统Gassmann方程进行流体替换,从而构建与频率相关的流体饱和岩石介质的定量岩石物理模型,以反映具有复杂孔隙结构特征的储层岩石,及其孔隙流体与固体骨架间的耦合作用对岩石地震弹性特征的影响,从而为不同频率测量数据的储层和流体解释提供一种方便的工具。
2. 试验样品制备与测量
试验使用的15块储层砂岩岩心样品均来自于新疆准噶尔盆地车排子地区春光油田的沙湾组。沙湾组主要为辫状河三角洲及滨海浅湖相沉积环境,以发育块状砂体为特征,具多个较大规模的低水位三角洲,总体属高孔、高渗储层。为使地震岩石物理研究有代表性,对目标储层(沙湾组2砂组)进行取样,取样井包括C2-5井、P201井等10口井,取样原则为确保样品能够覆盖目标层可能的孔隙度变化。根据样品的薄片和X射线衍射全岩心分析结果,样品以石英细砂岩为主,分选性较好;岩石成分以长英质为主,体积分数60%以上,胶结物主要表现为泥质、碳酸盐和石英胶结,体积分数小于30%;孔隙类型主要为原生孔隙和部分溶蚀孔隙,其中原生孔隙约占总孔隙的65%以上。从高孔隙到低孔隙,从点接触变为凸凹接触,反映压实作用增强(图1)。在样品对应的微米CT扫描图片中,高孔隙岩石样品(图1(b),H1砂岩样品,孔隙度f = 28.6%)在孔隙形态上表现为弹性性质较“软”的复杂多边形粒间孔隙,同时存在大量由接触边界或刚性颗粒压实破碎面所构成的弹性性质更“软”的孔隙;随着孔隙度的逐渐下降,孔隙形态也逐渐从多边形的软孔隙转变为近似三角形的“硬”孔隙(图1(d),H2砂岩样品,f = 13.9%),同时以颗粒接触边界为代表的软孔隙含量也明显减少。
由于试验样品取自10口井的不同深度,因此具有不同的压差(上覆地层压力与孔隙流体压力之差)。样品被制成符合试验标准的圆柱体(直径约25 mm,长40~50 mm),在洗盐、洗油和烘干等准备工作之后,采用CMS-300仪器测量模拟地层压差条件下的有效孔隙度。试验测试的干燥条件均指实验室干燥,即将烘干后的样品在潮湿空气条件下的露天放置24 h以上,得到约含有2%~3%水分的“干燥”样品,

Figure 1. The characteristics of micro-pore structures of reservoir sandstone samples
图1. 储层砂岩样品微观孔隙结构特征图
以消除黏土矿物脱水对岩石骨架弹性性质的影响。而水饱和样品则均采用抽空加压饱和的方法,饱和时间超过48 h,样品已达到完全水饱和状态。利用超声波脉冲穿透法测定样品速度,使用设备为成都理工大学“油气藏地质与开发工程”国家重点实验室的MTS储层岩石弹性参数测量系统,装置配套纵波PZT换能器的主频为800 kHz,横波主频为350 kHz。试验中,压力从2 MPa加至60 MPa,在10 MPa前每隔2 MPa测量一次,随后每隔5 MPa测量一次,压力点测量间隔15 min,以保证围压在样品中的平衡。水饱和条件下速度测量时孔隙压力始终保持在1 MPa的非排水状态,围压与孔压的压力偏差均小于0.3%。围压与孔隙压力分别通过两台ISCO高压无脉冲计量泵控制,围压通过连接压力釜体的ISCO高压泵控制,而孔隙压力则通过ISCO高压泵直接作用于样品表面,ISCO高压泵控制输入、输出流量,使液体压力达到预设值,并通过压力传感器进行计量。所用示波器时间测试误差 ≤ 0.01 μs,则测试系统速度测量相对误差的量级纵波约为1%,横波约为2%。
3. 样品地震岩石物理特征
图2(a)给出了研究区砂岩样品纵波速度随围压的变化,从变化形态上可以看出2种不同的速度变化趋势:第1种变化趋势以H10样品为代表,纵波速度随压力的增加呈近似线性的增加而无明显的非线性段,同时整个压力变化范围内纵波速度变化均小于5%;第2种变化趋势以H1~H9样品为代表,纵波速度均在压力较小(小于30~40 MPa)时迅速增加,在超过该压力时纵波速度变化较小并与压力呈近似线性关系,根据该类样品可大致认为研究区岩石中微裂隙闭合的有效压力应在30~40 MPa以上。第1种变化趋势表明岩石样品中主要以纵横比较大的刚性孔隙为主,反映岩石样品的“单一孔隙”结构类型。第2种变化趋势表明岩石中含有一定量的微裂隙,在压力作用下逐渐闭合,使纵、横波速度明显增加,反映岩石样品的“双孔隙”结构特征。Walsh [16] 讨论了围压与微裂隙纵横比的关系:
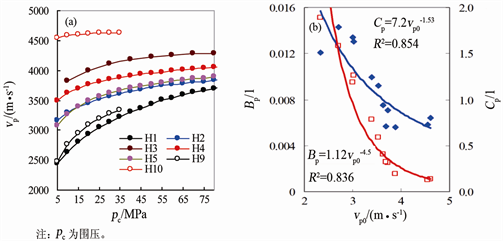
Figure 2. The variation of vp with confining pressure under dry condition of sample (a) and relationship between P-wave fitting Factor and vp (b)
图2. 样品干燥条件下纵波速度随围压变化(a)及纵波拟合因子与vp关系(b)
(1)
式中:pclose为裂缝闭合压力,MPa;Es为岩石基质的弹性模量,GPa;υs为岩石基质的泊松比,1;α为微裂隙纵横比,1。
对于砂岩样品,岩石基质的弹性模量为72.5 GPa,可粗略估计α平均约为0.001。
图2(a)中亦反映出研究样品速度随压力的变化率与其零压力速度关系明显,初始零压力速度越小,则速度随压力的变化率也越大;如H1、H3样品初始零压力速度分别为2423 m/s与3587 m/s,在干燥时整个压力范围内纵波的变化率分别为14.3、5.35 m/(s∙MPa)。图2(a)仅给出样品干燥纵波的变化特征,干燥横波及水饱和纵、横波表现为相同的变化规律。
通常,岩石的速度与压力的相关性可通过计算公式拟合:
(2)
式中:vpd、vsd分别为有效压力下干燥样品的纵、横波速度,m/s;pe为有效压力,MPa;vp0、vs0分别为干燥条件下初始有效压力时的纵、横波速度,m/s;Cp、Bp为纵波拟合因子,1;Cs、Bs为横波拟合因子,1;
为试验拟合参数 [17] ,1。
从拟合结果看,公式(2)对纵、横波速度与压力的拟合误差非常小,相关系数均接近于1。从图2(b)给出的Bp、Cp随vp0的变化关系可以看出:Bp与vp0呈明显的指数关系(
),在物理意义上Bp代表速度与压力变化关系线性段的梯度,vp0越大则其线性段的梯度越小,即速度随压力的变化较为缓慢;Cp与vp0也呈一定的指数关系(
),Cp反映低压力下非线性段的变化,正比于岩石样品中的微裂隙含量,vp0越大则固结与胶结程度越高,同时微裂隙含量也越低,Cp也越小,非线性段的变化也越不明显。
4. 岩石物理模型
4.1. 岩石骨架模型
4.1.1. 模型建立
砂岩的孔隙体系如果依据其孔隙结构的差异总能理想化为不同形状的硬孔隙与软孔隙(微裂隙)组合。基质中任意类型孔隙的加入都会改变岩石介质的等效刚度或者等效柔度。从静力学角度看,孔隙的加入形成附加应变,从而改变岩石的等效柔度,其物理意义更为明确。因此,在表征孔隙度及孔隙形状对岩石弹性性质影响时,采用等效柔度表示方法相较于等效刚度表示方法更为准确,尤其是在孔隙或裂隙等软孔隙含量较高的情况下。假定岩石基质的柔度为S0,硬孔隙与软孔隙的加入所产生的附加柔度分别为ΔSstiff、ΔScrack,则岩石等效柔度S可表示为:
(3)
由于附加柔度的线性叠加性,具有双孔结构特征的砂岩其基质中孔隙的添加可以分成2个阶段:
第1阶段,将硬孔隙加入基质中,如果考虑孔隙间的相互作用,则岩石介质的等效弹性模量按其柔度形式可用Mori-Tannaka公式计算 [18] :
(4)
式中:Kstiff、Gstiff分别为岩石介质的等效体积模量和剪切模量,MPa;K0、G0分别为岩石基质组成颗粒的体积模量和剪切模量,MPa;ft为总孔隙度,1;fs为硬孔隙的孔隙度,1;p、q为硬孔隙形状因子,是基质弹性模量与α的函数,1。
对于球形孔隙等规则孔隙,p、q可得到解析解;对于不规则孔隙,p、q可通过对弹性模量或速度的测量结果进行拟合得到。
第2阶段,加入软孔隙,岩石介质的等效弹性模量按其柔度形式仍可用Mori-Tannaka公式计算 [18] :
(5)
式中:Kd、Gd分别为加入微裂隙后的岩石介质等效体积模量和剪切模量,MPa;fc为软孔隙的孔隙度,1;P、Q为软孔隙形状因子,1。
如果将软孔隙看作微裂隙,在α小于0.1~0.2的情况下,裂隙自身的柔度与α无关,而是更多的取决于裂隙密度(ε),因此在考虑软孔隙影响时,可利用ε代替其孔隙度,两者关系为:
(6)
岩石中裂隙的形状极为复杂,而形状又对其柔度有明显影响,为使后续计算简化,采用简单类球体模型代替软孔隙形状,P、Q可给出解析表达式。同时,由于岩石中微裂隙的fc很小,公式(5)可表示为:
(7)
式中:υstiff为仅含硬孔隙时的岩石介质泊松比,1。
由于硬孔隙随压力变化较小,仅含该类孔隙的岩石介质,其等效弹性模量与高有效压力下的体积模量和剪切模量(Kh、Gh)近似。综合公式(5)、(7),可计算岩石样品的等效弹性模型。
4.1.2. 模型试验
公式(4)中,p、q分别代表硬孔隙的形状因子,根据试验结果可给出p、q与春光油田沙湾组砂岩岩心样品ft的经验关系。假定样品在80 MPa下的弹性模量代表岩石样品中仅含刚性孔隙时的弹性模量(即微裂隙全部闭合),利用公式(4)则可求出p、q,其结果见图3。由图3可以看出,p、q在1:1线附近,表明p、q近于相等,p、q与f亦具有较为明显的线性关系(
),利用该关系式可计算一定孔隙度下的p、q。
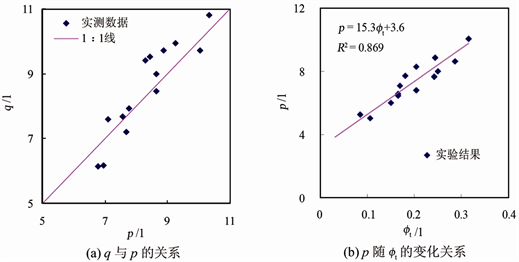
Figure 3. The relationship of pore shape factor of sandstone samples in Shawan Formation of Chunguang oilfield
图3. 春光油田沙湾组砂岩岩心样品孔隙形状因子关系图
图4(a)给出了H2样品总孔隙(ft)随pc的变化关系,通过该变化曲线可求取不同pc下的ft,ft随pc的变化是硬孔隙与微裂隙共同逐渐闭合的结果(ft = fc + fs)。在高围压下,样品ft的变化主要受硬孔隙的逐渐闭合影响,此时ft随pc变化亦表现为线性趋势,将该线性趋势外推至低压力范围,从而得到不同压力下的fs (如图4(a)中的红色虚线所示),不同压力下实测孔隙度减去对应fs即可得到对应fc。从试验结果看,样品的fc (零压力条件下)与ft (零压力条件下)呈明显的指数关系(
),表明对于所研究的中、高孔隙度砂岩,其孔隙度越高,所含的微裂隙也越多(图4(b))。据公式(6)可计算样品零压力的微裂隙密度(ε0),该值与ft呈明显的线性关系(
) (图4(c))。
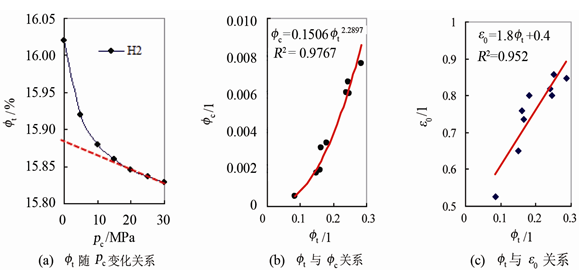
Figure 4. The feature of pc Change with ft and the relationship between ft, fc and ε0
图4. H2样品ft随pc变化特征及ft与fc、ε0关系
微裂隙密度随有效压力的变化可表示为 [17] :
(8)
式中:ε(pe)为有效压力下的微裂隙密度,1;此处的pe在干燥条件下等价于pc。
取碎屑砂岩的υstiff = 0.146 [17] ,公式(7)可简化为:
(9)
图5(a)、图5(b)分别给出干燥试验样品在20 MPa与50 MPa压力条件下纵、横波速度随孔隙度的变化规律,同时给出按公式(9)所计算出的理论模型值,可以看出,在2个试验压力下,理论模型计算结果与实际测量结果符合率均较高。当试验压力高于50 MPa时,纵、横波速度随压力的变化较弱,使得50 MPa时的理论模型计算结果,与高于该围压的实际测量结果有较好的一致性。
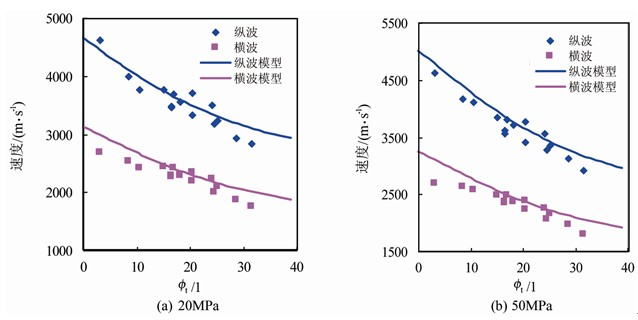
Figure 5. The comparison of measured vp, vs and theoretically calculated results under different pressures
图5. 不同压力条件下纵、横波速度测量结果与理论模型计算结果对比
4.2. 孔隙流体作用
在微观孔隙尺度下,流体流动作用对岩石介质弹性性质的影响可用喷射流理论描述。对具有双孔隙结构的岩石,弹性波的频散和衰减主要是由岩石中的微裂隙决定。在众多喷射流作用理论表述中,唐晓明给出了岩石介质中微裂隙与孔隙并存的弹性波同一理论,并将喷射流作用与岩石中ε与α两个重要孔隙结构参数建立了联系。利用相同的孔隙结构模型,Gurevich将喷射流作用与岩石中fc与α联系起来 [5]。在Gurevich的方法中,延续了Murphy与Dvorkin的思想,考虑了微裂隙中流体弛豫作用对其柔度的影响。如果将Kh (该模量为岩石中不含微裂隙的干燥体积模量)加入微裂隙,并考虑其与硬孔隙中流体喷射流作用影响时,介质等效模量Kmf、Gmf可通过下式计算 [15] [19] :
(10)
式中:Kd(pe)、Gd(pe)分别为一定有效压力下岩石介质的干燥体积模量与剪切模量,MPa;ω为圆频率,rad/s;η为孔隙流体动态黏度,mPa·s;αc为微裂隙特征纵横比,1。
公式(10)等号右端第二项也可理解为加入特定纵横比微裂隙并在考虑喷射作用下对Kh的改变。在考虑微裂隙作用后,剩余硬孔隙因其不可压缩性,在流体饱和后仍满足Gassmann方程,此时硬孔隙完全饱和时的体积模量Ksat与剪切模量Gsat可用下式计算 [15] [19] :
(11)
式中:Kf为混合流体体积模量,MPa;K0是岩石基质组成颗粒的体积模量,MPa。
总体建模思路见图6:第一步,在得到主要组成矿物含量的条件下,通过Voigt-Reuss-Hill岩石物理模型计算平均等效颗粒模量K0、G0;第二步,利用孔隙与压力变化试验关系,并结合公式(8)计算样品中的软、硬孔隙的孔隙度;第三步,依据非接触模型(公式(9))计算干燥岩石弹性模量;最后,依据Gurevich喷射流模型进行流体替换计算(公式(11)),得到考虑喷射流作用的速度频散模型。
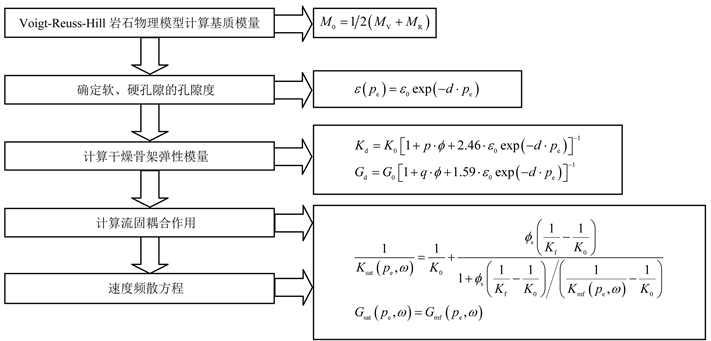 注:M0为岩石弹性模量,MPa;MV为利用Voigt公式计算得到的岩石弹性模量上限,MPa;MR为利用Reuss公式计算得到的岩石弹性模量下限,MPa。
注:M0为岩石弹性模量,MPa;MV为利用Voigt公式计算得到的岩石弹性模量上限,MPa;MR为利用Reuss公式计算得到的岩石弹性模量下限,MPa。
Figure 6. The procedures of seismic rock physics modeling based on porosity and pore shape
图6. 基于孔隙度与孔隙形状的地震岩石物理建模流程
为了验证上述速度频散模型的适用性,将H1与H5砂岩样品在700 kHz频率下测量的饱和岩石速度与模型计算的理论饱和速度进行了对比(图7)。图7中“干燥”表示岩石干燥速度测量值,“饱水”表示水饱和速度测量值。不难看出,岩石速度频散模型计算结果与实际测量结果符合度更高,而Gassmann方程计算结果在整个压力范围内均与测量结果存在明显差异。
5. 结语
地震岩石物理模型是建立储层特征与地震特征的桥梁,也是进行岩性和烃类预测的依据,而岩石物理模型的准确性取决于对岩石骨架地震弹性性质以及流固耦合作用的准确表征,因此,符合特定目标
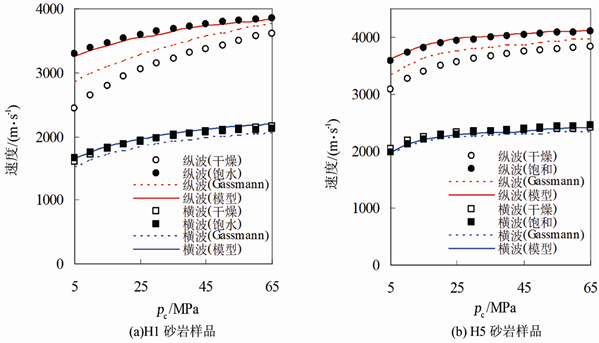
Figure 7. The interpretation of ultrasonic experimental results
图7. 超声实验结果解释
储层特征的岩石物理模型至关重要。
该次研究以新疆车排子地区春光油田沙湾组储层砂岩岩心样品实验室测试结果为基础,利用Mori-Tanaka非接触模型,提出了综合考虑储层砂岩孔隙度、孔隙形状以及微裂隙孔隙度对干燥岩石骨架弹性性质影响的地震岩石物理模型;模型中的参数均通过试验进行求取和标定,大大降低了建立储层岩石骨架弹性性质模型的复杂性和不确定性。
利用孔隙尺度喷射流作用模型替代传统Gassmann方程进行流体替换,既可以用于实验室岩石超声波测量数据的模拟和解释,也可用于地震测量数据的模拟和解释,从而为不同频率测量数据的储层和流体解释提供了一种方便的工具。
基金项目
国家自然科学基金项目(41374135)。