1. 引言
本文采用Nevanlinna理论中的一些基本概念和标准符号 [1] [2] 。亚纯函数通常指定义在整个复平面上的亚纯函数。设f是亚纯函数,用
表示亚纯函数f的增长级,用
表示亚纯函数f的超级,且定义如下
定义集合
的线性测度为
,以及对数测度为
。如果亚纯函数a满足
,其中
,那么称a是f的小函数,可能需除去一对数测度有限的例外集。设f和g为非常数亚纯函数,a为任意复数,如果
与
的零点相同并计重数,则称f与gCM分担a。如果f与g的极点相同并计重数,则称f与gCM分担
。
潘勒韦方程是一类物理背景深厚且应用广泛的重要方程。近十年来,人们通过引入Nevanlinna 理论深入研究了复域微分和差分方程,并取得了一些优秀的成果。随着Halburd和Korhonen [3] 以及Chiang和Feng [4] 的奠基性研究型成果的出现,促进了差分的Nevanlinna理论的建立以及潘勒韦差分方程的发展。而后,Halburd [5] ,Ronkainen [6] ,张继龙 [7] 等人对非线性差分方程进行了分类,给出了几类差分Riccati方程和潘勒韦I-V型差分方程。
设
均是f的小函数,记
是关于z亚纯,关于f有理的函数,其中
,并且
的次数分别为
。
汪晓明 [8] 等人研究了潘勒韦III型差分方程
的有限级超越亚纯函数解的唯一性,证明了在一定条件下,如果潘勒韦III型差分方程的有限级超越亚纯解f与另一个亚纯函数g有两个不同的有限分担值并且有完全相同的极点(计重数),那么
。
1991年,Ramani [9] 考察了潘勒韦IV型差分方程
,其中该方程的所有系数均为常数且
是关于z有理的函数。
本文,我们将
推广至
,进而研究了以下潘勒韦IV型差分方程
(1.1)
的有限级超越亚纯函数解的唯一性问题,又置
(1.2)
我们得到了如下定理:
定理1.1:设f是差分方程(1.1)的有限级超越亚纯函数解,g是一个亚纯函数,
为正整数且满足
。
为两个互异的有穷复数,
如(1.2)所示,若f和gCM分担
,且
,则
。
2. 引理
首先,亚纯函数f的差分多项式
定义如下:
(2.1)
其中,J是指标集,
是复常数,
是非负整数,系数
是f的小函数。对
的每一个单项式
,定义其次数为
。并定义
的次数为
接下来,为证明定理1.1,我们需要下列一些引理。
引理2.1 [10] 设f是超级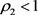 的非常数亚纯函数,c是一非零有穷复数,则存在正数
,使得
的非常数亚纯函数,c是一非零有穷复数,则存在正数
,使得
对所有r成立,至多除去一个对数测度为有限的集合。
引理2.2设f是超级
的超越亚纯函数,且满足差分方程
,其中 如(2.1)所定义。设a为f的小函数且满足
,则
如(2.1)所定义。设a为f的小函数且满足
,则
对所有r成立,至多除去一个对数测度为有限的集合。
证明:令
,并代入差分方程
中,于是得到
其中
,其每一项都是次数不小于1的关于g的多项式,且
,显然
,否则
,有
,即
,与题设矛盾。
接下来,我们来讨论
的情况。首先,记
,
,则当
时,由
其中
。再由引理2.1,有
则可得到
(2.2)
而当
时,
(2.3)
所以由(2.2)及(2.3),可得
得证。
引理2.3 [7] 设f是超级
的亚纯函数,且满足差分方程
,其中
如(2.1)所示,
是f的多项式,如(1.1)所示,若
则
。
引理2.4 [11] 设h为非常数整函数,
,
和 分别表示f的级和下级,
分别表示f的级和下级,
i) 若h为p次多项式,则
;
ii) 若h为超越亚纯函数,则
。
引理2.5 [11] 设
于开平面亚纯,
不为常数,
且满足
其中
。如果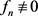 ,且
,且
其中
,则
。
3. 定理1.1的证明
由假设条件
及引理2.2,有
(3.1)
另外,由Nevanlinna第二基本定理
(3.2)
同理可证
(3.3)
所以
(3.4)
假设
(3.5)
其中,
是两个关于z的多项式。如果
,或者
,或者
时,则显然
。
下面假设
,
,且
。则由(3.2),(3.3)以及(3.5)可得
(3.6)
因此
。
令
,则由(3.5)式可得
(3.7)
或
(3.8)
于是由(3.7)可得
(3.9)
所以 ,又
,故
。
,又
,故
。
下面我们证明
。首先,我们假设
其中,
均为整函数,于是(3.7)可以写成
结合(3.1)式子可得
(3.10)
由条件
,所以由引理2.3有
,故
(3.11)
另外由第二基本定理可得
又
所以
(3.12)
同理可证得
(3.13)
于是,由(3.10)~(3.13)有
(3.14)
对(3.8)式类似分析可得
(3.15)
因此,由(3.14)及(3.15)可得
(3.16)
又由于
为非常数多项式,不妨设
,d是一个非零正整数,则由引理2.4及(3.16)式得
(3.17)
接下来,我们引入
,则将(3.7)式代入(1.1)式中得
又注意到
,于是等式两边同时乘以
,则可化为
(3.18)
令
,
,
,
。其中
均为次数至多是
的多项式,于是(3.18)整理可得
(3.19)
其中
不同时为零,
为关于
的多项式。
特别地,计算可知
(3.20)
于是,等式(3.19)两边同时除以
,并且移项得
(3.21)
不妨记
,则(3.21)可以写成
,其中q是一个有穷正整数。
而且,当
时,我们断言
事实上,当
时,则
是
和f的小函数,于是
又
所以
,矛盾,故
。
最后,由
的定义,有
,所以
。又
,其中
。所以由
,可得
,进而可以得到,对任意的
,有
于是,存在一个
,使得
故由引理2.5,可知
,即存在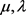 ,使得
,使得
即
,矛盾,故假设不成立。
至此,定理1.1证毕。
基金项目
本论文得到福建省中青年教师教育科研项目(JA15394)和福建自然科学基金项目(2018R0038)的资助。