1. 引言
捕食–食饵间的相互作用在生物界无处不在,也是生态学最重要的经典课题之一,许多学者通过建立数学模型研究了这种关系(Fan [1] , Hsu [2] , Jost Ellner [3] , Xu [4] , Wang [5] , Abrams和Ginzburg [6] , Huang [7] )。
捕食–食饵模型的功能反应函数经常被用来描述捕食者捕获食饵的能力。而Beddington-DeAngelis功能反应函数体现了捕食者内部存在干扰效应,具有Beddington-DeAngelis (下文统一称为BD模型)功能反应函数的捕食–食饵模型可以表示为:
(1)
这个数学模型由Beddington [8] [9] 独立提出。BD功能反应函数和著名Holling II功能反应函数类似,但在分母中有一个额外的cy,它体现了捕食者之间的相互干扰作用。在Skalski和Filliam [10] 的数学模型中,通过比较具有3种不同捕食者功能反应函数的19个捕食–食饵系统得到的统计资料,发现捕食者内部具有干扰关系的功能反应函数能很好的描绘捕食者对食饵的捕食情况,即BD功能反应函数相对于其他的功能反应函数能很好的描述捕食者对食饵的捕获(见Cantrell和Coser [11] ,Hwang [12] ,Liu和Zhang [13] )。
最近,许多文献研究了能够反应不同生命阶段的种群模型(见Aiello和Freedman [14] ,Al-omari和Gourley [15] ,Liu [16] ,Liu [17] ,Ou [18] )。通过对不同生命阶段种群模型的研究,发现具有不同生命阶段的种群模型具有以下的一些特征:幼年捕食者从出生到成熟具有一定的时间间隔,称这个固定的时间间隔为捕食者的成熟期。Liu和Beretta [19] 考虑了成熟时滞;幼年捕食者通常被它们的父母养育大,或者依赖于营养的供给,幼年捕食者不具有捕获食饵的能力,也不具有生殖能力,成年捕食者具有繁殖能力。幼年捕食者在幼年时期存活下来即可达到成熟阶段。如果幼年捕食者的死亡率不为0,那么仅有部分幼年捕食者可以进入成年阶段。因此,构建具有阶段结构的捕食–食饵模型就显得现实且有意义。Liu和Beretta [20] 构造了具有BD功能反应函数的阶段结构捕食–食饵模型:
(2)
其中,
和
分别表示食饵和成年捕食者的密度,
表示幼年捕食者的密度;b和
分别表示捕食者对食饵的捕获率大小以及捕食者处理食物的时间;n是捕食者的出生率,
为非负常数表示捕食者之间干扰效应的大小;假设幼年捕食者的死亡率为
(整个幼年阶段),
表示成熟期。最终,他们得到了两个结论:捕食者和食饵持久共存,当且仅当在食饵极大丰富时,捕食者的补充率比捕食者自身的死亡率高即可;如果系统是持久的,那么捕食者之间足够大的干扰不仅能使系统更加稳定,还可以增加成年捕食者的出生率等。
在Liu和Beretta [20] 的文章里,对于食饵的增长率而言,他们仅仅考虑了增长率的情形,事实上当食饵的生存环境为鱼池时,那么对于食饵来说,食饵的定期投放及时变指数增长率就必须考虑进去,同时他们忽略了时变环境对种群的动力学行为的影响。在Cushing [21] 的文章里,指出有必要考虑具有周期性生态参数或者扰动的模型,这样的模型是符合实际意义的,比如季节性的天气变化,食物供给,交配习惯,猎杀或者季节性收获等等。Yang和Shi [22] 建立了3阶段结构的捕食–食饵模型,系统中全部参数都假定为周期系数,他们讨论了正周期解的存在性。但是周期性行为只是时变环境的一种特殊情况,在本章中我们就食饵具有指数增长率的情形同时针对系统参数为更一般的时变情形做了定性的分析(当然包括了周期性的情况)。
2. 模型的建立
(3)
其中第一个公式中的函数
表示食饵具有时变补充率,
表示食饵的死亡率。其他函数
的表示意义分别为捕食者的捕获率、捕食者处理食物的时间、捕食者之间的干扰效应、捕食者的出生率、幼年捕食者的死亡率以及成年捕食者的死亡率。
3. 准备工作
首先,为叙述并证明主要结果,在此给出系统(3)的一些假设和符号说明。系统(3)的基本假设为:
(A1) 函数
为
上的正的有界函数且连续;
(A2) 若函数
为
上的连续有界函数,则
,
.
(A3) 存在正的常数
,使得
,
(A4) 对于所有
来说,都有
。
系统(3)的初值条件为:
(4)
其中对所有的
,有
使得
且C表示从
到R3上的连续映射的全体构成的Banach空间
元素
在C上的范数为:
其次为得到系统(3)的持久性与灭绝性的充分条件,在此给出相关的定义和引理。
定义3.1:系统(3)称为是持续的,若存在正的常数
及
使得
对系统(3)具有初值条件(4)的任意解
均成立,且
及
不依赖于初值条件(4)。
引理1 [23] :考虑下面非自治线性系统
(5)
假设(A1)与(A2)成立,则
1) 方程(5)具有初值
任意解的最终极限
在
内有界且全局一致吸引;
2) 存在常数m使得
;
3) 若方程(5)是ω-周期的,则方程(5)存在唯一非负ω的周期解且全局一致吸引;
4) 对任意的
,
,若
则方程(5)具有初值
的任意解
满足:
其中
模型解的正性和有界性
命题1:对任意
,系统(3)具有初值(4)的任意解
均是正的有界函数。
证明:由于系统(3)的右端是全连续的,因此系统(3)具有初值(4)的任意解
是存在且唯一的。
再由系统(3)可得:
(6)
若
则对任意的
总有
,显然对任意的
,
又
对任意的
有
。从而得到了
在
上的正性。因此当
时,对于任意的
,总有
。
最后证明对于任意的
,
有界。
令:
计算
沿系统(3)轨线的导数,可得:
(7)
令
,由(7)式可得:
由系统(3)的第一个方程,当
时,可得
。
应用文献 [22] 中的结论以及比较原理,可得存在
,当
时有:
(8)
进而
(9)
故存在
,当
时,有
(10)
因此,
是一致有界的,运用(6)式可得
也是一致有界的。故命题1得证。
由命题1的证明过程可知,对任意的
,系统(3)具有初值条件(4)的任意解
均是正的有界函数,从而紧集
是正不变的且在
中的正轨道为一致吸引的。
4. 主要结果
定义
接下来我们将会证明
,
对于捕食者的一致持久性和灭绝性的重要性。
4.1. 当
时捕食者的一致持久性
引理2 (见Song和Chen [24] )已知下述式子成立:
中a,b,c和
是正常量,当
时
。可得结论:
1、如果
,则
;
2、如果
,则
。
定理3.1:假设系统(3)满足初始条件(4),且满足 ,
, ,则捕食者就是一致持久的,即:
,则捕食者就是一致持久的,即:
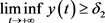 ,
,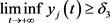 (11)
(11)
证明:第一步:假设 是系统(3)具有初始条件(4)的一个正解,由系统(3)的第一个方程,可得:
是系统(3)具有初始条件(4)的一个正解,由系统(3)的第一个方程,可得:

对所有的 成立。由比较原理和引理1中的结论(4),可得存在常量
成立。由比较原理和引理1中的结论(4),可得存在常量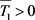 ,使得:
,使得:
 (12)
(12)
由系统(3)中的第二和第三个公式可得:
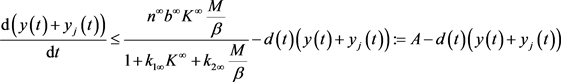
其中 。应用比较原理以及引理1中的结论(4)可得,存在常量
。应用比较原理以及引理1中的结论(4)可得,存在常量 ,使得
,使得
 (13)
(13)
对所有的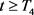 成立。
成立。
由系统(3)的第一个方程和不等式(13)可得:
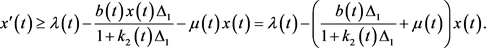
当 时,由比较原理、假设(A3)、引理1中的结论(4)可得,存在常量
时,由比较原理、假设(A3)、引理1中的结论(4)可得,存在常量 ,使得:
,使得:
 (14)
(14)
对所有的 成立。
成立。
第二步:

首先证明存在某个常量 ,
, 的取值不不依赖于系统(3)中的任何一个正解,从而:
的取值不不依赖于系统(3)中的任何一个正解,从而:
 (15)
(15)
如果(15)不成立,则存在系统(3)的正解 ,使得:
,使得:

从而,存在常量 ,使得
,使得 对所有
对所有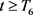 成立,其中:
成立,其中:
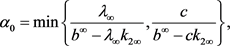 (16)
(16)
这里, ,
, 。
。
由系统(3)的第一个方程可得,对任意的 ,
,

运用比较原理可得:
 (17)
(17)
对所有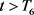 成立。则存在常量
成立。则存在常量 ,使得
,使得 对所有
对所有 成立。
成立。
由系统(3)的第一个方程可得:对任意的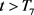 ,
,

由 ,从而
,从而 ,即
,即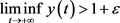 ,矛盾,从而(15)的结论是正确的。
,矛盾,从而(15)的结论是正确的。
为了得到 的一致持久性,将从以下两种可能情形进行讨论:
的一致持久性,将从以下两种可能情形进行讨论:
1) 存在 ,当
,当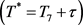
 时,使得
时,使得 。
。
2) 在
在 附近振荡,并对所有T成立。
附近振荡,并对所有T成立。
如果情形1成立,显然 是持久的。因此,这里仅考虑第二种情形。假设
是持久的。因此,这里仅考虑第二种情形。假设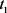 、
、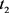 足够大且满足:
足够大且满足:

如果 ,那么
,那么 以及
以及 隐含着:
隐含着: ,
, 。
。
如果 ,由于当
,由于当 时
时 ,可知
,可知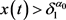 对所有
对所有 成立,因此可得
成立,因此可得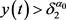 在
在 上成立。如果此结果不成立,则存在
上成立。如果此结果不成立,则存在 使得
使得 ,
, ,
, 对所有
对所有 成立。由系统(3)中的第二方程,令
成立。由系统(3)中的第二方程,令 ,可得:
,可得:
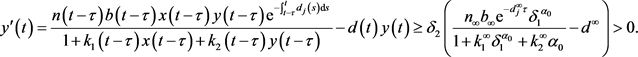
矛盾,从而 在
在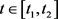 成立。
成立。
第三步:

由系统(3)中的第三个方程及上述结果,可得:

从而,由定理1可知,捕食者是一致持久的。
4.2. 时捕食者的灭绝性
时捕食者的灭绝性
定理2:如果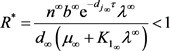 成立,则系统(3)中具有初值条件(4)的成年捕食者是灭绝的。
成立,则系统(3)中具有初值条件(4)的成年捕食者是灭绝的。
证明:由(5)式可知,存在 ,使得当
,使得当 时,
时, 。
。
从而:

令

由 ,以及文献 [25] 中的引理,可得
,以及文献 [25] 中的引理,可得 ,应用比较原理,最终可得当
,应用比较原理,最终可得当 时,
时,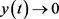 ,显然也有
,显然也有 ,从而证明了成年捕食者的灭绝性。
,从而证明了成年捕食者的灭绝性。
5. 数值模拟
很多因素都可以影响物种的持久生存,其中之一就是物种本身种群规模的大小,物种自身的成熟期会影响到物种的种群数量,倘若幼年捕食者的成熟期较长,很可能会导致捕食者的灭绝,这一结论与Gourley和Kuang [26] 文献中针对具有Holling II功能反应函数的模型讨论结果类似。考虑系统(3)中的所有参数为周期或一般时变的情形,进行了数值模拟。
图1:展示了系统(3)解的持久性,参数选取如下:
 ;
; ;
; ;
; ;
;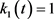 ;
; ;
; ;
; ,
, ,
, ,
, 。
。

Figure 1. Basic behavior of solutions of system (3) with 
图1. 系统(3)在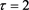 时的解的基本性态
时的解的基本性态
图2:展示了系统(3)成年捕食者的灭绝性,参数选取如下:
 ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ,
, ,
, 。
。

Figure 2. The mature predator in system (3) is extinct
图2. 系统(3)中的成年食饵是灭绝的
图1和图2分别展示了当幼年捕食者的成熟期为 时,捕食者与食饵的持久共存性以及成年捕食者的灭绝性,不仅对本章所得结论进行了验证,并且还弥补了文中没有证明系统解的持久性这一点。
时,捕食者与食饵的持久共存性以及成年捕食者的灭绝性,不仅对本章所得结论进行了验证,并且还弥补了文中没有证明系统解的持久性这一点。
6. 结论
本章研究了食饵具有时变指数增长率且捕食者具有阶段结构的非自治捕食–食饵模型,模型综合考虑了时变、非自治、捕食者的阶段结构等因素,本文不仅给出了模型解的正性和有界性,还给出了捕食者的灭绝性的结论。在证明系统解的一致持久性结论中,由于捕食者之间存在着干扰效应,模型中所有参数为时变参数,给定性分析系统解的一致持久性带来了困难,但依据比较系统理论知识以及通过定义捕食者的净再生数等方式,仍然给出了捕食者的一致持久性证明。通过数值模拟图形可以发现,当幼年捕食者的成熟期固定时,倘若幼年食饵的死亡率增加,并且成年捕食者的出生率降低,则会导致捕食者的灭绝。故在实际的生物系统中,对于那些种群繁殖环境恶劣,幼年捕食者存活率低的种群,其种群的持久生存面临极大的考验。
致谢
在此特别感谢哈工大的刘胜强教授以及哈尔滨师范大学的李冰博士对本文前期工作的支持,与两位学者交流的过程中收获了很多益于本文写作的建议。