基于VECM的教育投资与经济增长关系研究

Research on the Relationship between Education Investment and Economic Growth Based on VECM

摘要: 教育投资增加的一个物质基础，在增强社会各方面教育投资能力方面发挥重要作用。本文以中国1985~2017年为例，通过建立VAR以及VEC模型，采用Johansen协整分析和脉冲响应等方法，实证分析了教育投资与经济增长之间的关系，结果表明：我国教育投资对经济增长的拉动作用大于经济增长对教育投资的拉动作用，且经济增长对教育投资的促进作用具有一定的时滞性。

Abstract: As a part of human capital, the increase of education investment in expenditure will directly affect the development of the entire social economy. Similarly, the economy, as a material basis for in-creased investment in education, plays an important role in enhancing the investment capacity of education in all aspects of society. Taking China’s 1985-2017 as an example, this paper empirically analyzes the relationship between education investment and economic growth by establishing VAR and VEC models, using Johansen cointegration analysis and impulse response methods. The results show that education investment plays a greater role in promoting economic growth than the role of economic growth playing in education investment in China, and economic growth has a certain time lag in promoting education investment.

1. 引言

现今，世界经济逐渐向知识时代迈进，以知识和人才为主的要素已经成为当今世界各国经济竞争的核心要素，经济的增长也不再只是依靠有形资产的增长。由于教育投资不仅自身能形成递增的收益，还能使与之相关的作为要素投入的劳动、资本等也产生递增的收益，从而能够使整个经济都产生向上的规模收益。然而，我国的教育投资现状与经济发展现阶段的要求是缺乏协调性的。经济发展中以及随之而来的诸如城乡收入差距加大、教育投资分配不均等问题也凸显出来，这些因素共同作用导致我国教育投资支出和经济发展水平之间出现不相适应的现象。要妥善解决经济中出现的结构失调、转型升级困难，城乡差距拉大等问题，实现经济持续健康发展，改善落后地区经济状况，其中一个重要的手段即是加大对其教育投资的力度和改善投资结构 [1] 。本文拟从教育经费支出与经济增长(一世纪GDP为衡量标准)角度实证研究二者的相互关系。

2. 相关文献综述

从20世纪60年代初开始，以传统的经济理论为基础，舒尔茨(美)用教育收益率法，丹尼森(美)用因素分析法，斯特鲁米林(前苏联)用劳动简化法研究了教育和经济的关系，得出教育投资与经济增长相互促进的结论。此外，舒尔茨通过引用美国教育投资的相关数据，实证研究了教育投资对经济增长的关系，分析了各级教育投资收益率和教育投资占比的问题 [2] 。

我国对教育投资与经济增长二者关系的研究起步则相对较晚(约1985年开始)。中国经济学会(1984)的成立和《教育与经济》杂志(1985)的创刊，对我国教育经济学的出现具有里程碑意义。王善迈的研究在这一期间备受关注，其在著作《中国教育经费面临的问题与对策》中，从教育经费的比例问题入手，发现了我国高教生均费和普教生均费的区别，并指出我国在三级生教育的投入上居世界前列 [3] 。李玲通过对小学和中、大学的在校生数和教育投资数进行比较，发现我国存在教育投资结构失调问题 [4] 。杜晓利、沈百福引用我国1993~2006年间数据，通过研究预算内教育经费的分配状况，得出财政预算内教育经费在高等教育方面的分配比例合理，而在中等教育中的分配不合理的结论 [5] 。近年来，随着计量方法的拓展和计量软件的开发，对教育投入(作为人力资本)和经济增长(作为物质资本)的研究不断创新，如温以萍、包吉祥 [6] ，方超、黄斌 [7] ，顾芸 [8] 均采用空间计量的方法，实证研究我国经济增长与教育投入的关系，发现二者之间存在失衡性。孟望生、姜莱 [9] 通过面板回归方法实证研究了人力资本投资和物质资本回报率的相互关系。

从以往对这方面的研究成果来看，我们能够发现：一方面，对教育投资和经济增长的关系研究，更多的集中在教育投资对经济的单向促进作用，对二者双向关系的研究则较少。另一方面，对促进经济增长的研究大都与教育投资的数量挂钩，反而忽略了教育投资的质量和平衡度的问题。此外，教育投资的不断增长也产生了一些意想不到的结果，如巨大的教育投资支出可能会“挤占”消费结构中的其他方面，进而又会降低人们的生活质量 [10] 。

本文运用向量自回归模型(VARM)以及向量误差修正模型(VECM)，选取Wind资讯库以及《中国统计年鉴》中的相关数据(时间跨度为1985~2017年)，通过Johansen协整检验的方法确定VECM，并采用脉冲响应分析的方法，探讨教育投资和经济增长二者相互影响的内在关系。

3. 模型构建和统计分析

本文数据引用Wind资讯库以及《中国统计年鉴》中我国1985-2017年教育经费(记为EA)和GDP不变价(记为GDP)相关数据，样本量为33。

3.1. 平稳性检验

首先，为消除异方差和多重共线性问题对时间序列平稳性的影响，并缩小数据之间的差距，对所取数据进行了对数化处理。其次，在建立模型之前采用ADF法对涉及的变量数据进行单位根检验，以确保序列平稳性，如表1。

Table 1. ADF testing process

表1. ADF检验过程

从表1的检验结果可以看出，变量LN_EA、LN_GDP均为非平稳序列，但经一阶差分(序列DLN_EA、DLN_GDP)后呈平稳状态，说明二者都是一阶单整过程，即I (1)。

3.2. VAR模型建立及最优滞后阶数确定

VAR (Vector Auto Regressive)模型由Sims (1980)提出，是当今世界上分析经济系统动态性的主流模型之一。VAR模型可以表述如下：

$Y_t={\alpha }_1{Y}_{t-1}+{\alpha }_2{Y}_{t-2}+\cdots +{\alpha }_p{Y}_{t-p}+{\epsilon }_t$ (1)

其中，Y_t为被解释变量，Y_t-1~Y_t-p为Y_t的1~p阶滞后期(p为模型的滞后阶数)；ε_t为随机项。本文将DLN_EA和DLN_GDP作为内生变量并分析二者之间的相互影响关系，建立模型VAR(2)，令：Y_t = (DLN_GDP_t，DLN_EA_t)，将模型检验结果写成如下矩阵形式：

$Y_t=\left[\begin{array}{cc}-0.143& -0.011\\ 0.568& 0.498\end{array}\right]\ast Y_{t-1}+\left[\begin{array}{cc}-0.163& -0.126\\ 0.461& 0.551\end{array}\right]\ast Y_{t-2}+{\epsilon }_t$ (2)

从该估计结果可以看出，滞后一期和二期的DLN_GDP对当期DLN_GDP和DLN_EA均有负向影响，这说明GDP的增加对教育经费的支出并没有体现出很强的拉动作用；而滞后一期和二期的DLN_EA对当期DLN_GDP和DLN_EA均有正向影响，说明教育经费的增加会对经济增长具有正向拉动作用，且从相关系数的绝对值来看，这一拉动作用大于GDP增加对教育经费支出的带动作用。根据这一模型结果调整并确定最优滞后阶数，如表2。

Table 2. Optimal lag order determination

表2. 最优滞后阶数确定

本文根据表2的检验结果，结合AIC优先的准则，确定最优滞后阶数为3。下一步对DLN_EA和DLN_GDP建立模型VAR(3)，仍令：Y_t = (DLN_GDP_t，DLN_EA_t)检验结果如下：

$Y_t=\left[\begin{array}{cc}-0.112& 0.029\\ 0.334& 0.254\end{array}\right]\ast Y_{t-1}+\left[\begin{array}{cc}-0.140& -0.055\\ 0.305& 0.228\end{array}\right]\ast Y_{t-2}+\left[\begin{array}{cc}-0.152& 0.020\\ 0.494& 0.466\end{array}\right]\ast Y_{t-3}+{\epsilon }_t$ (3)

由上述估计结果可以看出，滞后一期、二期和三期的DLN_GDP对当期DLN_GDP均有负向影响，滞后一期和三期的DLN_GDP对当期DLN_EA有正向影响，这说明GDP增加对教育经费支出的带动作用存在波动和时滞性；滞后一期、二期和三期的DLN_EA对当期DLN_GDP和DLN_EA均有正向影响，这和估计方程(2)的结果一致。

3.3. Johansen协整检验及VEC模型建立

为检验变量之间的协整关系存在与否，本文运用Johansen协整分析方法，确定DLN_GDP和DLN_EA之间是否存在协整关系及协整方程的个数。检验结果如表3所示。

Table 3. Johansen cointegration test process

表3. Johansen协整检验过程

根据Johansen协整检验结果，迹统计量和最大特征值统计量均显示在5%水平下，DLN_GDP和DLN_EA之间存在一个协整方程，据此，建立VECM模型，其中协整方程ECM_t−1表示如(4)。

${\text{DLN\_GDP}}_{t-1}=0.223{\text{DLN\_EA}}_{t-1}+0.114$ (4)

将VECM估计方程写成如下表达式：

$\begin{array}{l}\Delta D\left({\text{DLN\_GDP}}_t\right)\\ =-1.623{\text{ECM}}_{t-1}+0.407D\left({\text{DLN\_GDP}}_{t-1}\right)+0.200D\left({\text{DLN\_GDP}}_{t-2}\right)\\ -0.221D\left({\text{DLN\_EA}}_{t-1}\right)-0.155D\left({\text{DLN\_EA}}_{t-2}\right)-0.003\end{array}$ (5)

$\begin{array}{l}\Delta D\left({\text{DLN\_EA}}_t\right)\\ =-0.108{\text{ECM}}_{t-1}+0.102D\left({\text{DLN\_GDP}}_{t-1}\right)+0.011D\left({\text{DLN\_GDP}}_{t-2}\right)\\ -0.740D\left({\text{DLN\_EA}}_{t-1}\right)-0.477D\left({\text{DLN\_EA}}_{t-2}\right)-0.005\end{array}$ (6)

方程(5)、(6)即为依据协整方程而得到的VECM的矩阵形式。从协整方程(4)来看，教育投资每增加1单位，会引起GDP增加0.223个单位。从VECM方程来看，滞后一期和二期的DLN_GDP对当期DLN_GDP和DLN_EA均有正向影响；滞后一期和二期的DLN_EA对当期DLN_GDP和DLN_EA均有负向影响。

3.4. 脉冲响应分析

为进一步发现GDP和教育投资之间的相互影响程度，本文采用脉冲响应分析(包括DLN_GDP对DLN_EA的冲击响应和DLN_EA对DLN_GDP的冲击响应)的方法，首先对一阶单整序列DLN_GDP和DLN_EA进行AR根值法来确定序列的稳定性，检验结果如图1。

Figure 1. AR root test results

图1. AR根检验结果

由图1可以发现所选变量的根模均落在单位圆内，因此平稳性检验通过。考虑DLN_EA对DLN_GDP的冲击，响应期设定为10期，脉冲响应结果如图2。

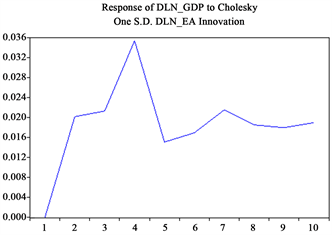
Figure 2. Impulse response of DLN_EA to DLN_GDP

图2. DLN_EA对DLN_GDP的脉冲响应

由上图可以看出，教育投资在前4期对GDP的冲击较大，GDP上升的速度较快，从第4期开始逐渐下降，但总体趋势是上升，说明教育投资对GDP增加存在正向拉动作用。考虑DLN_GDP对DLN_EA的冲击，结果如图3。

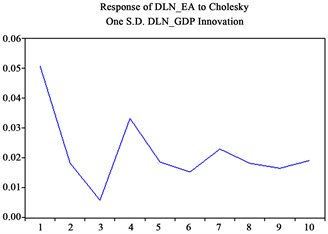
Figure 3. Impulse response of DLN_ GDP to DLN_EA

图3. DLN_GDP对DLN_EA的脉冲响应

从图3可以发现，GDP对教育投资的冲击表现为：教育投资总体波动下降，但始终为正。这说明GDP对教育投资的拉动作用并不明显，这与方程(2)、(3)的检验结果一致。

4. 结束语

经过上述数据模型分析验证，本文得出以下结论：第一，教育经费的增加会对经济增长具有正向拉动作用，且从VAR相关系数的绝对值以及协整方程系数来看，这一拉动作用大于GDP增加对教育经费支出的带动作用。第二，一定时期内，教育投资和GDP之间并不存在双向正相关关系，GDP对教育投资的拉动存在一定的时滞性，这一点在模型相关系数上表现为先负后正。

根据上述的研究结论，可以看到教育投资是影响中国经济增长的一个重要因素，而且长期来看两者之间存在一定关联。考虑到中国教育投资的现状，政府需要合理把握财政性教育投入导向和尽力确保教育经费总支出的结构比例均衡，以促进教育投入对国民经济增长的拉动作用，这也是下一步需要改进的工作，即在模型中加入教育投资质量和平衡度等控制变量。

基金项目

本论文受到山东省社会科学规划研究项目“山东‘高精尖缺’人才引进机制与对策研究”(16CGLJ34)，山东省社会科学规划项目“山东省企业创新路径与企业价值管理协同研究”(16CGLJ09)的资助。