1. 引言
上海同业拆借率(SHIBOR)是根据伦敦同业拆借利率(LIBOR)的模式,建立各大银行的拆借市场后出现的一种同业间的拆借利率,意义在于反映银行资金是否充足,为各行各业融投资提供一个宏观金融信息的参考。
关于SHIBOR时间序列指数的研究较多,但大体分为三类。第一类是SHIBOR时间序列在相关领域的应用。SHIBOR最为主要的应用是作为利率的基准,蔡卫光,张烨 [1] (2005)提出SHIBOR时间序列是利率市场化的决定因素,并进行了两数据之间的协整分析。张丽娟 [2] (2007)对银行间货币利率市场进行了研究。张一中 [3] (2009)论述了SHIBOR时序与中国利率市场化的关系。陈汉鹏,戴金平 [4] (2014)提出将SHIBOR时间序列作为中国基准利率,并进行可行性研究。当然SHIBOR不仅可以作为利率的基准,也可以作为许多相关领域的参照,如债券,风险投资等。第二类是对SHIBOR时序的影响因素的分析,李海涛,王欣,方兆本(2008) [5] 提出了基于偏t分布对SHIBOR隔夜拆借利率影响因素进行了分析。潘松,魏先华,张敏,宋洋,陈敏 [6] (2009)论证了银行间支付流对SHIBOR时序的影响。陆伟伟 [7] (2017)对我国SHIBOR影响因素进行了相关的实证分析。第三类研究是关于SHIBOR时序的自身研究,何梦泽 [8] (2013)基于GARCH模型对SHIBOR的波动率进行了分析,高薇 [9] (2015)基于GARCH族模型对SHIBOR金融市场进行了类似的分析。上面是对SHIBOR波动率的分析,同时也说明了SHIBOR时序是条件异方差的。在SHIBOR定价方面的研究,于建忠,刘湘成 [10] (2009)基于一般的资产定价函数,对SHIBOR定价理论模型进行了研究。但运用Levy过程,对SHIBOR时序数据进行分析与探讨的文章较少。
众所周知,SHIBOR时间序列数据随着时间的变化而发生波动与改变,而且某一个时间段的信息大小也会影响到SHIBOR时间序列。在金融模型中,一般时间带来的波动是比较稳定的波动,可以用布朗运动进行拟合。但商业时间不等于普通时间,它有时也称内在时间或本质时间。它反映的是随着商业周期或市场条件不断转变,带来影响的因素。在商业时间的问题上,相关的金融学学者提出了多种解决方法。比较早期的是Heston [11] (1993)提出的随机波动率模型,他令其BS模型中的波动率服从一个CIR均值回复过程。后来许多研究者都围绕随机波动率进行了大量研究,Bate [12] (1996)以Heston模型为基础引入了Merton [13] (1976)随机跳模型,其认为随机波动率应该受多个风险源的影响。Chacko和Viceira [14] (2003)同样认为波动率应该有多个频率与波幅,采用单因素波动率只会扭曲原来的经济现象。S. R. Hurst与E. Platen [15] (1999)提出了内在时间,并尝试运用对数稳态过程来拟合内在时间带来的波动。
基于前人研究思想与模型,本文提出基于Levy过程模型进行SHIBOR时间序列分析。文中使用的Levy过程模型相比其它模型有以下几个优点。一是可以更好地进行路径拟合,这是因为Levy过程比较丰富,可以根据自己的需要与数据特点不断进行调整拟合,选择不同的Levy过程。而且Levy过程具有无限可分性,便于建立模型后参数的检验与校准。二是可以引入各种Levy跳过程,并将其视为商业时间带来的影响,而将布朗运动视为一般时间带来的影响。三是大部分Levy过程都有自己的特征函数,可以根据Fang和Oosterlee [16] (2008)提出的Fourier-cosine series理论进行其衍生品定价。在研究思路与方法方面,四是本文采用的模型较之随机波动率模型与其它时变模型,参数较少,而且随机项也比较少,这样可以较好地应用于实际工作。使用Levy过程模型进行SHIBOR时间序列路径刻画,是本文最主要的创新。这样不仅可以解释条件异方差的问题,同时赋予波动率一定的经济含义。在参数估计方面,本文应用极大似然估计方法。对于参数有约束条件的,采用内点罚函数的方法去掉约束,然后运用模拟退火的方法实现全局最优。在实证检验时,采用蒙特卡罗的方法进行模拟,同时运用均方误差最小为指标进行检验。本文接下来的结构如下:第二部分进行一般性统计描述,第三部分是相关的模型介绍,第四部分是参数估计与检验,最后部分是结论。
2. SHIBOR时间序列统计特征
SHIBOR时间序列有八个指标,分别为隔夜、一周、两周、一个月、三个月、六个月、九个月与年数据。为了对SHIBOR进行较好的研究,在统计分析上,我们采用了2013以来的数据,其时间序列路径如图1。

Figure 1. Path of SHIBOR time series
图1. SHIBOR时序路径
不难得出,年数据在较长一段时间都趋于平稳状态,是最平滑的数据且波动最少的数据,而隔夜数据是波动最多的数据,其他时间序列数据都随着间隔日期变长而趋于平稳与平滑。
接下来分析它们的基本统计指标,本文选取了六个基本统计指标,分别为最大值,最小值,均值,标准差,偏度与峰度,具体数据见表1。

Table 1. SHIBOR time series six major statistical indicators
表1. SHIBOR时间序列六大统计指标
从表1的数据分析得出,隔夜数波动区间最大,而年数据的波动区间最小。在均值方面,隔年数据的均值是最小,年数据最大。从而可以得出,隔夜数据波动幅度最为剧烈。在标准差方面,一个月期限的标准差最大,隔夜数据居中,而年数据最小,不难得出,隔夜数据在数据波动幅度较大的基础上,它的波动频率较小,或者它出现大波动的次数较低,多为小波动。从偏度的角度分析,隔夜数据偏度最大,其值为3.303932,存在明显右偏,即有一个较长在拖尾在密度函数左边,这种统计性质反映在金融时间序列模型中就是不对称跳。隔夜数据的峰度为26.34744,也是所有时间序列中最大的一个,说明其存在严重的尖峰。综上分析,可以得出,隔夜数据是时间序列中最难处理的数据,不仅波动幅度大,而且存在尖峰,厚尾,有偏与不对称跳等一般金融模型不易处理的性质。在本文的分析中,我们采用隔夜数据时间路径作为研究对象。采用隔夜数据的原因有两点,其中最主要的一点是因为市场信息能及时在隔夜数据中得到反应,另外一个原因是其时间路径在研究上不易处理。接下来分析了隔夜数据的样本密度函数与分布函数,见图2与图3。

Figure 2. Density function of SHIBOR
图2. SHIBOR的密度函数
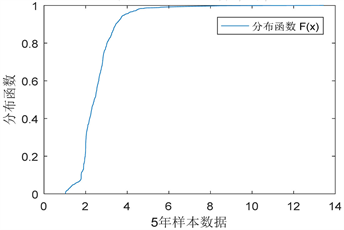
Figure 3. The distribution function of SHIBOR
图3. SHIBOR的分布函数
从图2与图3分析,SHIBOR时间序列无论是密度函数,还是分布函数,都是极其不规则的。从密度函数来看,其有两个极峰,而且密度函数出现多处波纹。在模型方面,这是极难拟合的。从分布函数的角度分析,其大部分样本在2到4之间,但其尾部极其不对称,随着样本值变大,存在严重的拖尾现象。
综上分析,经典的B-S模型很难拟合上述的统计性质,因此,需要引入新的过程B-S模型,借以更好拟合SHIBOR时间序列。
3. Levy过程模型
(一) Levy过程与Levy测度介绍
为较好拟合隔夜的SHIBOR时间序列,解决其尖峰、有偏,拖尾等问题,本文引入了默顿跳过程(MJ Process)、双指数跳过程(KOU Process)、正态逆高斯过程(NIG Process)、方差伽玛过程(VG Process)与α稳态过程(α stable Process)。关于Levy过程具体定义、性质与Levy分解本文不做过多详述,接下来主要介绍这几种Levy过程的测度见表2。

Table 2. Measure and characteristic function of five kinds of Levy processes
表2. 5种Levy过程的测度及其分布函数
(二) 具体模型介绍
默顿跳过程是由默顿 [13] (1976)提出,即在B-S模型的基础上,加入了一个复合跳过程。用其布朗运动的跳模拟合一般时间的波动,用复合跳过程模拟合商业时间的波动。引入默顿跳后模型结构如下:
其中
为模型的漂移项,t为时间,
为布朗运动,
是以
为期望的泊松过程,
为
为期望,
为方差的高斯分布。根据模型的表达式,可以推出其特征函数为
。
双指数跳过程是Kou [17] (2002)以默顿跳过程的思想为基础建立的Levy过程。与默顿跳的差别是不再假定跳跃幅度服从高斯分布,而是服从双指数分布。引入双指数跳后其模型结构为
,
其他假定为引入默顿跳后的模型一样,唯有
服从双指数分布。
中有四个参数,p > 0表示上跳的概率,
为跳跃强度,
与
分别为上跳与下跳的收敛速度。模型的特征函数为:
基于双指数跳的模型较之基于默顿跳的模型优点在于考虑了SHIBOR时间序列数据的拖尾与厚尾现象。
默顿跳过程与双指数跳过程都属于有限跳过程,另外三种跳过程都属于无限跳跃过程。Barndorff-Nielsen提出了正态逆高斯过程,也是目前金融学界应用较多的纯跳过程。由于它的混合密度函数服从逆高斯分布,因而得名正态逆高斯过程。正态逆高斯过程有三个参数(
),其中
是控制峰度的函数,
是控制偏度的函数,而参数
是控制跳跃尺度的参数,对整个分布的二阶矩有较大的影响。引入
正态逆高斯过程后其模型的特征函数为
。
正态逆高斯过程不仅能较好的控制跳跃过程的拖尾与尾部不对称,更能较好的拟合跳跃过程的偏度与跳跃尺度。
方差伽玛过程是Madan和Seneta [18] (1987)提出,并且他们 [19] (1990)论证了这个过程可由两个伽玛过程合成。引入方差伽玛过程后其模型结构为
,与前面定义相同,
为方差伽玛过程,它有三个
参数C,G和M。引入VG过程后模型的特征函数为
。大量实践证明,基于方差伽玛过程的模型能够更好地拟合金融数据的尾部分布。
介绍稳态过程之前,先介绍一下稳态分布。稳态分布的定义是根据中心极限定理定义的,即从一个随机变量X中取独立同分布
,如果存在正实数
,满足以下等价分布条件,即
,其中
表示等价分布,则称随机变量X服从稳态分布。
稳态过程的Levy测度为
。其中
与
分别为控制正负跳的参数,
表示跳跃幅度,
作为系数控制尖峰厚尾程度。基于
稳态过程Levy模型,其模型结构为
,其中
是
稳态过程。Weron R. [20] (1995)与Nolan J. P. [21] (1998)提出
稳态分布涉及多个不同的参数系表征方法,在不同的参数系下,其特征函数表达式也不一样。本文引入的引入
稳态过程是在标准参数系下,引入
稳态过程后模型的特征函数为:
在以上几种Levy过程模型中,用Levy跳过程刻画商业时间给SHIBOR时间序列带来的波动。而商业时间给SHIBOR带来的波动在金融数据中反映为不对称跳,拖尾,尖峰等现象,引入的Levy跳过程也正能反映这一些问题。
4. 实证与检验
(一) 实证参数估计
以上五个模型,本文采用极大似然的方法进行了参数估计。除方差伽玛过程外,其他过程都较难找到其显示的分布函数。在估计时,需应用梯形法则,进行离散傅里叶逆变换,从而得到离散的密度函数。然后对离散函数对数化,再相加,可进一步得到其似然函数。最后通过优化工具,求得最优解。大部分优化工具仅能得到局部最优解,局部最优解不一定是全局最优解,因而采用了模拟退火的方法。
模拟退火的优化方法虽然可以得到全局最优解,但不能求解有约束条件的情况。采用的Levy过程部分有约束条件,在优化的过程中,不能直接对其进行优化,必须将有约束优化问题转化为无约束优化问题。我们采用了内点罚函数法,去掉了约束条件,使原来的问题变成了无约束问题。
运用上述的思想方法与2013以来SHIBOR时间序列数据,进行了参数估计,参数估计结果见表3~7。

Table 3. Parameter estimation based on Merton jump process model
表3. 基于默顿跳过程模型参数估计

Table 4. Parameter estimation based on double exponential jump process model
表4. 基于双指数跳过程模型参数估计

Table 5. Parameter estimation based on normal inverse Gauss process model
表5. 基于正态逆高斯过程模型参数估计

Table 6. Parameter estimation based on variance gamma process model
表6. 基于方差伽玛过程模型参数估计

Table 7. Parameter estimation based on α stable process
表7. 基于α稳态过程的参数估计
(二) 随机模拟
基于已经估计出来的参数,即可通过matlab软件随机生成路径。随机生成路径的方法有多种,最常用的一种是根据分布函数逆生成。每种算法都有自己的优势,而且算法研究也相当成熟,这里不再细述。将以上模型模拟路径结果抽样如图4。

Figure 4. Simulation path versus real path comparison
图4. 模拟路径与真实路径对比
在随机模拟路径的时候,为了直观,本文用英文大写字母表示引入特定Levy过程模型。同时也为了便于对比与接下的检验,我们将SHIBOR实际数据的起点也调整至0。
(三) 实证检验分析
无论从参数估计结果,还是观测其路径,都可以发现,自2013以来,SHIBOR时间序列的漂移项基本为0。一条随机路径就能从总体上判断模拟路径是否正确,并不能检验基于哪种特定Levy过程拟合较好。基于Levy过程的模型相比其它模型,有一个特有的优势——无穷可分性。因而可以天为单位,对路径进行截断,然后观察每一天上升与下降的数据。这样,一条SHIBOR时间序列路径就变成了1156个样本,基于这些样本,就可以在多种检验方法进行选择。
为了研究与对比以上几种路径,本文采用蒙特卡罗方法对5个基于Levy过程模型进行模拟,得出5条时间序列路径。然后采用同样的截断方法,以天为单位进行截断,得到1156个模拟样本。再将这些模拟样本结合原SHIBOR时间序列数据进行密度函数分析。
经过多次模拟,基本可以得到与图5类似的密度函数分布。由于将一条路径变成了1156个样本,样本容量相当充分。图5是整体密度函数效果图,图5附注是将趋于0的中心进行部分放大。从图5分析得出,无论是尖峰,还是厚尾方面,α稳态过程拟合最好,在尾部不对称与拖尾方面,正态逆高斯过程拟合最好,同样的结果也可以从分布函数图像图6观察出。但总体上分析,正态逆高斯过程的拟合效果并不理想。我们进行了均方误差最小的分析,模拟了1000条路径进行分析。模拟结果表明:除了正态逆高斯过程均方误差偏大,其余四个过程得出的均方误差水平一样,差距都在百分之一以内。
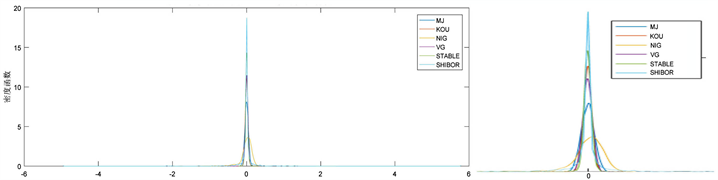
Figure 5. Analysis chart of Density function simulated sample and real SHIBOR sample
图5. 模拟样本与真实SHIBOR样本密度函数分析图

Figure 6. Analysis chart of distribution function of simulated sample and real SHIBOR sample
图6. 模拟样本与真实SHIBOR样本分布分析图
基于上述结论,也为我们今后研究提供了一些方向与引导—通过改进或整合Levy过程或给Levy过程增加更多的控制参数,使其更好拟合SHIBOR时间序列。
5. 结论
随着人民币利率市场化不断提出,许多学者都尝试着寻求人民币利率市场化后的参考指标。也正如VIX指数未出现之前,在学界已经开始研究。前面综述中列举了许多研究已然证明SHIBOR指数在人民币利率市场化后可以作为极其重要的参考,它也将在整个金融市场扮演更重要的角色。无论人民币利率是否市场化,SHIBOR指数都可以作为金融市场利率的一个基准,成为我国金融界或学界衡定收益率的一个重要参考指标。因此,对SHIBOR指数的研究也越来越重要。
本文基于B-S模型,引入Levy过程,借以拟合商业时间给SHIBOR时间序列带来的波动,从而达到更精准的预测SHIBOR时间序列的变化趋势,在我国目前的金融市场,具有较大的理论意义与现实指导作用:其一是我们根据Levy过程模型的特征函数,比较容易进行SHIBOR利率定价,从而设计出一系列的利率衍生品,通过交易衍生品,达到我们规避利率风险的目的。其二是由于SHIBOR利率与金融市场许多指标具有相关性,运用类似的方法,可以研究许多相关指标,这样可以对许多相应的金融指标进行检验与预测,对丰富我国金融市场的金融产品有着重要的指导作用。其三是模型相比其它模型,随机项与参数较少,减少了模型中的不确定性,能够更好地应用指导实际工作。
通过本文,还可以进行以下拓展,一是引入更为复杂的Levy过程,但更复杂的Levy过程参数也会更多,无论是估计、检验,还是误差与数值上的处理,都会带来更大的困难。二是结合SHIBOR利率,进行相关衍生品定价,对原有的模型进行校准。但由于我国金融体制尚不完善,许多相关的衍生产品都在起步阶段,难以找到大量数据进行定价校准。三是Levy过程模型中,结合金融市场的相关特征,引入时间序列模型,如ARMA,ARCH,GARCH族模型等。由于第二个拓展方向,在现在的中国市场很难获得数据,因而接下来我们只有从第一个与第三个方向开展研究工作,为推进SHIBOR时序的研究与完善金融市场做一些基础性的铺垫。
致谢
本文感谢西南财经大学四川省金融智能与金融工程重点实验室博士生尹亚华提供若干指导意见。