1. 引言
1982年,Feynman提出了量子计算机的想法,其目的是克服经典计算机在模拟量子力学过程中经典算法本质上存在的困难 [1] 。1994年,Shor提出了量子计算机的第一个量子算法 [2] ,用于求极大整数的因子分解,其效率明显优于目前的最先进的经典因子分解算法,但无法证明不存在经典算法比Shor量子因子分解算法更高效。1997年,Grover量子搜索算法横空出世 [3] ,打破了人们关于经典算法可以替代量子算法的疑惑 [4] 。Grover量子搜索算法可由量子线路模型和绝热量子计算两种等价的方法实现。简单地讲,量子线路模型通过各种通用量子酉门的时序组合来编码并求解得到最终结果;而绝热量子计算则通过制备初始哈密顿及其基态,并将结果编码进查询哈密顿的基态,在量子绝热定理的保证下来得到结果。本文从绝热量子计算角度来探讨Grover量子搜索算法,得到了其量子加速特性的一个必要原因,这一结果使得按照该算法的实质来设计其他量子算法成为可能。
2. 绝热Grover算法
在数据库中存在N个未排序的条目,这里N极大,目标是在这N个条目中找到指定的一个条目,并且查询的次数最少。处理该问题时,经典算法的平均查询次数为
,而Grover量子搜索算法的平均查询次数仅为
。对n量子比特Grover量子搜索算法,其可搜索的条目总数为
。按照绝热量子计算的方法 [5] ,初始哈密顿
为
这里1表示单位矩阵,平均态
表示初始时各条目
处于等同地位,被搜索到的概率都为
,同时
构成一组标准正交基。
假定
代表要搜索的结果,称为目标态,则将编码该目标态到查询哈密顿
为
则绝热演化哈密顿
就可以描述为
由于
与其他
都正交,故可将绝热演化哈密顿
在
与其正交态
构成的子空间上表示出来,有
令
则
有如下紧凑形式
能量本征值和相应的本征态分别为
这里我们稍作讨论,当
时绝热量子系统
,此时
是绝热量子系统的初始基态,相应的系统参数为
,当N足够大时,
意味着
;依据量子绝热定理,
应始终是绝热演化过程的基态,且当
时绝热量子系统
并查询到目标态
,相应的系统参数为
,意味着
。由于绝热演化的基态
是绝热量子计算唯一关心的态,那么我们将它稍作调整,令
,则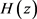 变为
变为
相应地,
变为
(1)
这样的好处是当
时绝热量子系统处于平均态
上,而当
时则恰处于所要查询的目标态
上。下面我们说明由(1)式所描述的绝热基态与变分法中广为熟知的最速降线问题的联系并给出本文结果。
3. 绝热Grover算法与最速降线问题
首先,我们给出Hilbert空间的最速降线问题。
问题:给定N维Hilbert空间
中的两个量子态
,寻找一条测地线
使得
,其中
是关于
的一个指标泛函。
上述问题是变分法中的最速降线问题在Hilbert空间中的一般描述,它的提出与绝热量子计算是有联系的,因为实际上问题中的
和
分别对应绝热量子计算的平均态
和目标态
,找到了最速降线也就找到了使得平均态
到达目标态
的最快路径。问题的核心在与如何确定指标泛函
,而这需要考察量子态的物理。
由于归一化量子态的物理等价性,即
和
描述的是同一个物理态,因此对于N维Hilbert 空间
的归一化非零子集
而言,我们需要引入复投影空间
及其伴随的投影映射
,使得
,这里
。而复投影空间ℂP上两相邻两物理态
和
间的度规恰是Fubibi-Study度规,即
这里
表示量子态
的局域协变导数。不难验证Fubibi-Study度规是U(1)
局域规范不变的。而连接Hilbert空间中的两个量子态
和
间的最速降线
在复投影空间ℂP上的投影
也应是物理态
和
间的最速降线,故指标泛函
可定义为
这里
表示Hilbert空间的范数。计算
为
根据变分问题的条件
并考虑归一化条件
所给出的约束条件
,那么依Lagrange未定乘子法可得,
(2)
其中
是待定参数。对方程(2)左乘
并利用归一化条件
,不难得到
,事实上
因此惨数
是常数。进一步地,方程(2)具有局域U(1)规范形式不变性,即当
时,方程(2)变为
这里
。这表明满足具有局域U(1)规范形式不变性的方程(2)的任意曲
线都是最速降线,它们在复投影空间ℂP上的投影相同。方程(2)在满足量子平移条件
时又可化为
(3)
从微分几何和量子几何相位的角度讲,满足方程(3)的各量子态都具有与初始量子态相同的相位。令
,则对如下常微分方程的边值问题,
这里
,其解为所要求的最速降线,即
(4)
比较(1)式和(4)式,若令
,则不难发现Grover量子搜索算法有明显的量子加速效果的一个
必要原因是其绝热量子计算方法中的绝热演化基态恰处于一条连接初始平均态
和目标态
的最速降线上。
4. 结论及展望
本文从变分法中的最速降线问题的角度出发,利用变分法的成熟方法,得到了绝热Grover算法的绝热基态的演化路径是在由单一目标态和其正交态构成的子二维Hilbert空间中的一条最速降线,这也是Grover量子搜索算法有明显的量子加速效果的一个必要原因。文献 [6] 从量子信息几何的角度采用Wigner-Yanase度规研究了量子混态的情况,当其退化为量子纯态时与我们的结果相同。对于同时查询多个目标的问题,绝热Grover算法也可以实现,文献 [7] 从纯分析的角度给出了解答。然而,与查询单一目标的问题相比,多目标态和其正交态所构成的空间将更为复杂,绝热基态的演化路径也不再是一条曲线,但也可以通过最速降线问题来给出几何解释,只是几何解释的难度将加大。此外,运用变分法中的最速降线方法,我们还可以讨论近几年来热门的量子速度极限等问题 [8] 。