1. 引言
在传统市场中研究消费者的消费行为时,心理距离一直起着重要的作用。然而,在电子商务时代,其重要性受到质疑。一种普遍的观点认为“伴随着电子商务时代物流能力的巨大提升,空间距离(心理距离的一个组成维度)已经消亡,消费的做决策行为不再受其影响” [1] [2]。对此,有学者对此持否定观点,他们通过实证研究指出,在电子商务时代传统的心理距离仍然在发挥作用,空间距离的作用并没有消亡 [3] ,相较而言,变化的是心理距离的组成成分和作用形式 [4]。对心理距离的研究,意义之一体现在其对消费决策的影响上。通常来说,心理距离的大小可在一定程度上反映出消费者做决策的难易程度。心理距离越小,消费者越容易做出消费决策,反之,则越不容易做出消费决策 [5] - [12]。
最近,经济学家们对电子商务环境下消费者的心理距离进行了广泛而深入的研究,他们发现心理距离的确出现了一些新的特征和属性,但旧有的属性内容依然存在。特别地,电子商务环境下心理距离旧有的消费行为标识功能仍然存在,即消费者与商家之间的心理距离越小,就意味着交易越容易实现。Benedicktus [5] 通过统计分析有实体店的网店交易量与消费者心理距离之间存在的相关性,证实了这一论断。Kim等人 [6] 则通过实证研究发现,在线消费者的时间距离和社会距离(心理距离的两个组成维度)之间交互影响起作用,而并非各维度独立起作用。当时间距离和社会距离较接近,低解释水平价值因素对消费者评价影响相较于时间距离和社会距离较远时的高解释水平价值因素对消费者评价的影响要大。进一步地,Huang等人 [8] 通过统计分析在线消费者对餐厅的评论数据,发现各维度心理距离对解释水平和在线评论均有影响,且各维度之间存在着交互影响,具体表现为,一个维度对解释水平和在线评论的影响会促进另一个维度对解释水平和在线评论的影响。
为了更好地运用电子商务时代的心理距离内在规律特性服务于电子商务的健康发展,人们对心理距离的变化规律和测量方法进行了研究。例如,为了研究在线共同体验者心理距离增大的规律,Lim等人 [13] 建立了心理距离与共同体验间的关系模型,实证研究了共同体验者心理距离的变化规律及其影响因素。为了统一电子商务环境下消费者心理距离的测度方法,黄等人 [14] 以解释水平理论为基础系统分析了电子商务环境下消费者心理距离的组成维度,通过整合以往心理距离的测量方法,构建了新的心理距离测度指标体系,给出了完整的距离指数。同年,Wang等人 [15] 改进了Huang等人提出了在线消费者心理距离的测度公式,并实证研究了消费者在书籍,电子产品等消费品上与不同B2C零售商之间的心理距离。结果表明,不同物品,消费者与商家之间的心理距离不同。
然而,以上的研究内容几乎都只是定性地讨论了电子商务环境下在线消费者的心理距离的相关课题。从在线消费者心理距离对消费决策的影响,心理距离各组成维度间的相互作用,心理距离变化影响因素分析到心理距离测度方法的系统研究,均未深刻揭示出电子商务时代心理距离的性质和特点,因而也无法为电子商家制定更佳的营销策略提供切实可靠的指导。为此,本文建立了一个关于在线消费者心理距离和消费决策间的关系式。运用这个关系式,我们能较为准确地测算出消费者与商家间的心理距离,据此预测出在线消费者的决策行为。这使商家能够预知消费者消费决策,从而使制定出更具针对性的营销策略成为了可能。
本文的内容组织如下。第二部分简要回顾了模型的理论基础最大熵原理;第三部分是模型建立主体部分,建立了消费决策和心理距离之间的关系模型;第四部分对模型进行了验证分析;第五部分总结了全文,并指出本文工作面临的挑战。
2. 熵与最大熵原理
熵是由玻尔兹曼在研究热力学问题时首次提出的用于度量一个系统的不确定性的重要概念 [16] ,与事件发生的概率有紧密的联系,可由如下表达式简单表示,
(2.1)
式(2.1)所表达的意思是指,宏观状态的熵S等于该状态发生概率的对数与玻尔兹曼常数k的乘积。至今,熵理论已普遍应用于各种有序的和无序的数量变化和现象迁移方面的研究 [17] - [22]。
上世纪五十年代,Shannon [23] 在系统研究前人工作的基础上,创造性的提出了用于度量带噪信道中通信信息损失量的熵概念——Shannon信息熵,该名称由冯诺依曼建议使用,此后一直沿用至今。信息熵比热力学熵更具有广泛的含义,可与许多现实事物紧密联系起来。如下就是信息熵和广义熵之间存在的一个经典关系式:
(2.2)
式(2.2)中H是指系统的Shannon熵,K是一个常数,与系统自身相关,
表示在该系统中状态i出现的概率 [24] [25] [26]。
基于Shannon信息熵的发现,Jaynes [27] 提出了最大熵原理,此进一步拓展了信息熵的应用范围。其主要思想是,对一个系统增加一些约束条件后,或者当该系统的信息不完备时,可以用熵最大来度量该系统所处的性态。最大熵原理是一种具有学科交叉性质的模型建立方法,可运用于构建和求解些概率系统问题,加之其与贝叶斯方法往往在分析问题时表现相似或相近的结果,现已成为人们进行统计推断的重要工具。
通常而言,一个系统的信息熵最大意味着该系统处于最混乱、最不稳定的状态,而这恰好与现实世界中真实的系统所处的状态吻合,非常高精度的诠释了当前系统的性态。现实中的不确定性有两种来源,一种源于概率不确定性现象,另一种则源于确定性现象。在线消费者购买决策行为中的不确定性是个概率事件,购买和不购买属于概率性行为,然而在消费决策之前,电商事先无法知道具体的购买行为;即使对于确定性现象,事件结果也是既定的非概率事件,具体结果是什么,仍然事先无法得知。最大熵原理描述的是概率不确定性现象。需要指出的是,这里的概率是从主观解释的角度而言的,与通常所说的以一个事件发生的频率作为发生概率表示的客观解释不同。主观解释的概率观点认为概率分布是一种知识表达,可进行独立观察。
信息熵的类型由随机变量的类型决定,按随机变量类型划分,最大信息熵有两种类型,一种是离散型的,另一种是连续型的 [23] [28] [29] :
1) 离散型
设X是一个离散型随机变量,其可能的取值及其对应的取值概率分别为
和
,那么Shannon信息熵可以表示成
(2.3)
其约束条件为
(2.4)
若随机变量X的期望E已知,则约束条件(2.4)将重新变成为
(2.5)
2) 连续型
当X为连续型随机变量时,设其概率密度函数为
,那么 Shannon信息熵式(2.3)将表示成
(2.6)
其约束条件为
(2.7)
如果随机变量X的期望E已知,则约束条件(2.7)将改写成如下形式,
(2.8)
值得指出的是,以上不同的约束条件式(2.4),(2.5),(2.7),(2.8)会对应不同的拉格朗日函数表达式(这里的格朗日函数由目标函数、约束条件和朗格朗日乘子综合构成),从而会分别得到不同的模型结果。例如,随机变量的一阶原点矩已知而二阶原点矩未知时,模型结果呈指数分布形式,而当随机变量的二阶原点矩已知而一阶原点矩未知时,模型结果则呈正态分布形式。读者欲了解更多关于模型的细节,请参阅 [30] [31]。
3. 心理距离与决策行为关系模型构建
为了将复杂的现实问题化简转变成可建模问题,从而建立具有一定理论和现实意义的数学模型,我们先给出如下两个假设:
假设1:总购买量和总访问量都由心理距离唯一决定,不受其他因素和位置差异的影响,即当心理距离的大小一样,则对应的总购买量和总访问量就一样。
备注1:前人的研究结果表明,在收入等要素相一致的条件下,心理距离的大小能以较高的可信度反映出消费者做消费决策的难易,心理距离越小越容易做出消费决策,而心理距离越大越不容易做出消费决策。所以,在不考虑收入等要素的情况下,我们提出了假设1 [5] - [12]。
假设2:总购买量和总访问量满足可数可加性,即指总购买量等于各部分购买量之和。
备注2:假设2是基于数学加法原理的假设。一个简单的例子如是,一条绳子的重量等于将其分割成n段后的各段绳子重量之和。然而假设2的内容并非这么直观易解,它假设在一个平面上分散在各点的购买量,访问量之和分别等于总购买量和总访问量。
下面是模型建立的详细内容。为书写方便,从本部分开始,我们假设心理距离X是一个取值在一个给定的范围内的非负随机变量,
表示随机变量X取长度x时的网站访问量,
是取长度x时的购买量。由心理距离的概念及其对消费决策的作用知,
和
是关于心理距离的单调函数,这与建立城市人口分布模型的条件相似 [32] [33] ,因此本文运用相似的方法建立模型。这里,我们仅考虑
是单调减函数的情形(事实亦如此,心理距离越大消费者越不容做出消费决策,也即对应网站访问量减少)。需要指出的是,本文建模所采用的方法对单调递增函数同样适用,对于这种情形只需将原函数
取相反函数
来进行表示即可。
受Clark关于城市人口密度建模的启发 [32] [33] ,我们考虑在一个半径任意大的圆面上用
表示距离圆心为r的网站访问量(这里还可以将
理解成距圆心r远处的网站访问量密度)。从圆心画一条足够长的线段便将其分割成足够短的
段,将每一段的网站访问量对应的记为
,
此时若将总网站访问量记为P,则有
。将网站总访问量的P状态数在该线段上表示成
一个有序分割问题,则得如下形式,
(3.1)
由此即有此线段上的网站访问量信息熵表大式,
(3.2)
其约束条件表示为
(3.3)
(3.4)
这里
表示总网站访问量,现实中其值可在网站后台查询得到。
为便于运用最大熵原理求解式(3.2),建立如下的Lagrange函数,
(3.5)
这里
和
是相互独立的Lagrangian常数,对充分大的P和
,运用Stirling公式
和运用极值条件
,由式(3.5)得
(3.6)
考虑随机变量为连续型变量的情形,分别用r和
替换i和
,将式(3.6)带入到式(3.4)中转化成如下的积分式,
(3.7)
对充分大的圆半径R,运用L’Hospital法则进行化简,并结合式(3.6)得,
(3.8)
此时取
,得对应的网站总访问量
(3.9)
据此,设
为特征半径,定义:
(3.10)
此表示在距圆心为
的区域内的网站访问量为网站总访问量的一半。结合式(3.8),(3.9)和(3.10)即得,
(3.11)
注意到心理距离的长度与各构成维度间满足如下的关系式 [15] :
(3.12)
这里
分别表示心理距离,时间距离,社会距离,空间距离,
分别代表各维度对应的权值。关于心理距离各维度的具体定义可参阅 [15]。用
分别表示
。
结合式(3.11)和式(3.12),我们得到如下的关于网站访问量和心理距离长度的关系式,
(3.13)
同理,用
替换
,并进行类似计算和推到,又得和式(3.11)。
相似的结果,
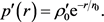 (3.14)
(3.14)
进一步地,进行同上述替换一样的有限步替换,最终我们又可得到如下的消费量和心理距离间的关系式,
(3.15)
结合式(3.13)和式(3.15),我们得到如下的关于消费率和心理距离间的关系式,
(3.16)
此式表明在线消费者的消费决策与心理距离间的关系可用清晰的数学关系式来表征。
备注3:式(3.7)中积分下限为0仅仅出于方便数学表达的考虑。在实际计算中,积分下限可根据具体情况取任意大的正数。
4. 模型验证
基于黄等人的工作 [15] ,我们选取Tmall,JD.COM和Amazon上具有代表性的主营书籍和数码产品的六家店铺为研究对象。当有人访问网站时及时问卷调查时间距离,社会距离和空间距离,收集必要的数据,并进行无量纲化处理 [14]。
具体地说,对来访者问卷“预期决策与实际决策之间的时间长度”作为时间距离,其测度见下表1。
社会距离通过问卷来访者“在线消费者与网络商家之间的亲密程度”打分得到,其测度见下表2 (来源: [14] )。

Table 2. Measure of social distance
表2. 社会距离测度表
空间距离用“消费者感知到的与网络商家之间的距离”来表征,可近似用从消费者下单到收货的时间跨度来表示,其测度见下表3 (来源: [14] )。

Table 3. Measure of spatial distance
表3. 空间距离测度表
对按照以上三个表进行处理得到的数据我们运用Matlab拟合式(3.18)中的曲线得如下参数估计值(表4)。

Table 4. Results of fitting curve in (3.18)
表4. 式(3.18)的曲线拟合结果
上表中Parameters从左到右分别表示
,Residuals值为曲线拟合残差。上表显示该曲线拟合效果好。
注意到式(3.18)中含有四个变量,消费率为因变量,剩下的时间变量,社会变量和空间变量为自变量,这就导致无法在现实中画出拟合曲线图(现实中最多只能画出三维图,四维图是不存在的)。为了充分利用图形来分析和理解该模型,我们将式(3.18)的四维图形分割成三个三维图形来进行研究(这里的距离指标采用了 [14] 中的结论)。
由以上三个图可知,三个自变量(时间距离,社会距离和空间距离)对购买率都有反方向作用且影响程度各不相同。也即,随着这三个自变量的增大,购买率呈下降趋势,并且当时间距离和社会距离中至少有一个量取值变化率很大时(表现为取值具有跳跃性),购买率将出现剧烈的下降趋势,然而当空间距离取值变化率很大时,购买率的下降趋势却不显著。此意味着前两个距离对购买率的影响较空间距离的影响大。而且从图1、图2和图3中可知,时间距离对购买率的影响较社会距离对购买率的影响大,所以当给定空间距离,同样大小的时间距离和社会距离将获得不同的购买率,前者下降比后者快。综合得知,心理距离对购买率的影响大小顺序为时间距离,社会距离和空间距离。
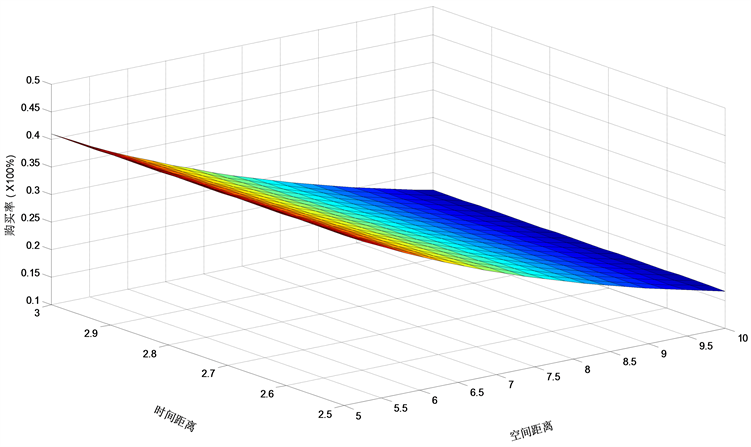
Figure 1. A decreasing surface meaning the relation between purchase rate and time distance and spatial distance
图1. 购买率与时间距离和空间距离的关系图,其中竖坐标表示百分比,理解时需乘上100%,显示的是一个单调下降的曲面

Figure 2. A decreasing surface meaning the relation between purchase rate and social distance and spatial distance
图2. 购买率与社会距离和空间距离的关系图,其中竖坐标表示百分比,理解时需乘上100%,显示的是一个单调下降的曲面
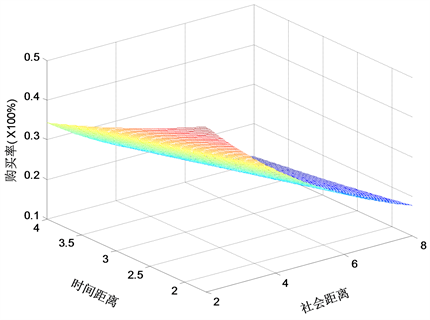
Figure 3. A decreasing surface meaning the relation between purchase rate and time distance and social distance
图3. 购买率与时间距离和社会距离的关系图,其中竖坐标表示百分比,理解时需乘上100%,显示的是一个单调下降的曲面
5. 结论
当前,对在线消费者的心理距离的研究主要集中在心理距离在电子商务环境下的概念变化,心理距离对电子商务的影响及其原因,并未涉及它们之间的数量关系。本文我们首次运用最大熵原理建立了消费决策和心理距离之间的一个新的关系式,并对模型进行了分析。结果表明,消费决策与心理距离之间存在负指数关系,即消费决策随心理距离的增加呈负指数下降,而不是简单的线性下降;心理距离的三个组成维度中,时间距离维度对消费决策的影响最大,其次是社会距离维度,最后是空间距离维度,这与已有的研究结果相符。同时,该模型的建立弱化了商家预知消费决策的难度,即在心理距离已经测定的条件下,运用这个模型商家就能预测出消费者的消费决策趋势,这为商家更好的制定出具有针对性的电子商务营销策略提供了一个新的思路。
然而,不管是从理论上还是从实践上,我们的研究也面临一些挑战。在建模中,我们运用了一些数学上的技巧简化了模型,这就很难避免引起误差的增大。除此而外,式(3.18)中的参数不容易测量,这也造成了误差的进一步增大。
基金项目
国家自然科学基金全面上项目(71271207)。