1. 引言
拉伸试验是确定材料机械性能的基本试验。假设变形前后试件的密度不变原则下,研究延展性和收缩量的偏差和颈缩,有一定的价值 [1] [2] 。本论文用推倒来算出真实收缩率和收缩率间的关系,分析了两者间的偏差。收缩率偏差大则它的真实性大,即收缩率变大。延伸率偏差小于收缩率,真实值变小。这在工程应用方面有利,因为我们不需计算即可知道曲线。在偏差较大区间,需换成真实值。所以一定范围内的偏差值变化规律是这次研究的内容之一 [2] 。因为颈缩是拉伸实验的最后一环,它的延伸率会大于前面延伸变形之和。但从45#中碳钢试件的拉伸试验结果分析来看颈缩阶段的延伸率没有那么大,也不是很小。其断面收缩率变化显著,它与延伸率相当甚至更大。这可能就是宋玉泉所说的“失稳” [3] ,所以我们研究颈缩是拉伸试验的比较重要的环节,比如许多断面收缩率大于延伸率2倍的状况是颈缩失稳引起的。如何理解断面收缩率大于2倍延伸率是本次我们研究的课题。
2. 计算结果
在试件中l0的一段称为标距,l为断裂后的标距测量长度。试件初始横截面积是S0,断裂后是S,d0为圆试件的初始直径,d是断裂后直径 [1] 。试件理论收缩率用ψ和延伸率用ε表示,公式为
(1)
(2)
由于
(3)
所以真实收缩率
(4)
即
(5)
由上可知收缩率的最大值小于1。真实收缩率
,则
大于0,故
之间为增函数,
大于0时
也大于0,即随着
的增加而
增大。在
小于10%时可用下式近似计算,即
(6)
3. 讨论
从图1可以看出,在趋势线下方收缩率偏差大。在收缩率偏差9%~109%区间即在
区间真实延伸率和延伸率偏差之比小于收缩率偏差之比。表1是收缩率在
和
时的偏差大小的数据分析。它说明随着延伸率的增大延伸率的偏差变大。当
为定值即图1左下角的位置0.09时和右上方1.09时随着延伸率的增大真实收缩率
也增大。真实收缩率与真实延伸率偏差在0.09时相差不大,但在1.09时相差1.83倍。这说明真实收缩率的真实度增大了近一倍。真实收缩率在这些偏差时后者是前者的近2倍,说明收缩率值在偏差增大后变得更真实。在延伸量逐渐加大的情况下收缩偏差大于延伸偏差,所以收缩偏差的真实性大。如图1所示,可以从曲线上清楚看到这一趋势。根据图中虚线可知在虚线上方延伸率偏差率值大,在虚线下方断面收缩率偏差率较小。即延伸率在上方真实性高,断面收缩率在下方其真实性高。在9%~109%区间断面收缩率的偏差率比延伸率的高,真实性高。从图1可以看出,偏差
与断面收缩率ψ之比随着断面收缩率的增大而增大。此俩方程式的曲线为一条近似直线,收缩率偏差比延伸率偏差大约成比例增加。收缩率的偏差在大于80时它的偏差大于延伸率的1.83倍,说明收缩率比延伸率真实约1.83倍。
规定了两种标准拉伸试样,
。这里有根据密度不变原则
,得
,又由
,得
,故得
(7)
对于圆拉伸试样,相应于
和
,分别称为10倍和5倍试样。相应地,延伸率分别用ε10和ε5表示,标距短延伸率则大。由图2可知设拉伸前标距l0内分为5等分,拉伸实验后除了中间为
为外,其余为
。当第3段里发生的颈缩为
,即
。如果拉伸前的此段在拉伸后成为
,由于2 > 1.8因此此段发生了颈缩,它的长度在此段没有超出过大范围,则最小值为
即为合格试件。如果颈缩大需相应增大倍数。如果颈缩断裂面在标距中央就直接测量l,如果偏移到距最近标距处
以内则可用移位法测量延伸率。研究颈缩发生区间就是探讨颈缩伸长量,以此进一步研究收缩率过大的原因。如果颈缩伸长量在
区间则认为收缩断口是产生了双晶形成较大的收缩量。
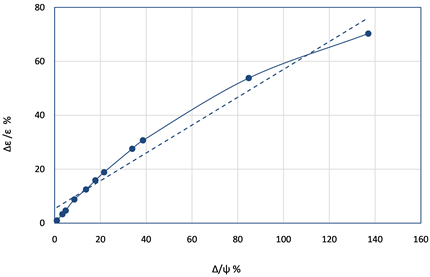
Figure 1. Relation between the true elongation deviation and the reduction deviation
图1. 真实和延伸率偏差之比和收缩率偏差之间的关系图

Table 1. Deviation of reduction between ψ t = 1.09 ψ and ψ t = 2.09 ψ
表1. 收缩率在
和
时的偏差大小
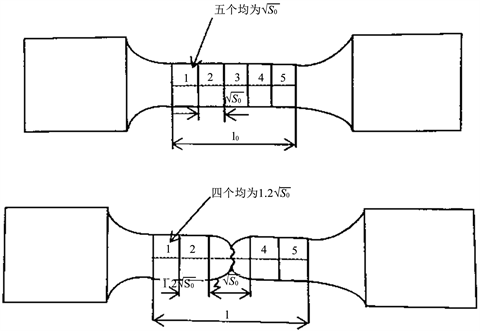
Figure 2. Variation of the specimen elongation before and after test
图2. 拉伸前后试件延伸率的变化,这里S0是初始面积
设拉伸实验后
为颈缩长度变化,
为其余部分长度变化。则
时发生颈缩,由于
可认为
(8)
为延性材料颈缩发生依据。如果
值变大颈缩变大,它跟ε的变化成正比。
ψ和
的关系曲线如图3。断面收缩率随着
减少,ψ从90%减少到0。
变小则试件面积S0变大断面收缩率变小。收缩率变大第一是因为试件尺寸外的外部条件,这时材料承载大,颈缩也大。第二是因为内部结构问题,这时裂纹经过的路径多而产生颈缩。这是试验负载和材料性质所致。从缺陷分析转位引起延伸率增加,双晶引起收缩率增加。

Figure 3. Relation of the reduction and
图3. 断面收缩率和
的关系
如宋玉泉 [3] 提出的失稳等难以解决的现象发生,单纯依靠数学关系来解决是不够的,需要对此进行全方位的调查才能应用到实际当中,解决问题并成为标杆作用。例如失稳就是断面收缩率在大于等于理论延伸率时发生,这与数学关系论证相违背,所以需注意到为什么会发生这种现象来定义才能分析并解决问题,这会在以后的论文当中进行探讨。甚至某些断面收缩率达到数倍理论延伸率值也会有其一定的因素起作用。
4. 结论
1) 在真实收缩率小于1.09倍ψ时真实延伸率和延伸率偏差之比小于断面收缩率偏差率之比,收缩率更真实。当真实收缩率大于2.09ψ时收缩率偏差又变大,当真实收缩率一定时收缩率变大,偏差也变大,收缩率也更真实。真实收缩率在0.09和1.09偏差时后者是前者的近2倍,说明收缩率值在偏差增大后变得更真实。当
为80时收缩率偏差比延伸率的偏差大,约1.83倍,说明收缩率比延伸率更真实1.83倍。
2) 对于延性材料延伸试件引起颈缩的范围为断面收缩率
或
,颈缩越大
越大。当
时整个收缩率
或达到
。随着颈缩继续变大
,此时
,甚至
。我们认为转位引起延伸率的增大,双晶引起收缩率增加。因为拉断时材料在外力或动载作用下会出现大的响声,由此判断一定数量甚至大量的双晶出现,我们认为它是颈缩失稳的主要原因。
基金项目
KOSEF (the Korea of Science and Engineering Fund) under the Specified base program 96-0300-11-01-3.
参考文献