1. 前言
在求解一些代数类问题,例如求出矩阵函数的解、求出矩阵函数的逆、解微分方程组,尤其是在求解常系数线性微分方程组初值问题的过程当中,运用矩阵最小多项式能达到简化运算和快速计算标准矩阵的目的。最小多项式同时也是多项式理论中的重要内容,它在矩阵对角化的判断、矩阵是否相似以及在线性变换结构中的研究都有相应的运用。最小多项式除了在矩阵理论方面有所应用,在线性控制系统等其他领域的应用十分也广泛。
2. 利用特征多项式求最小多项式
定义1.1 [1] :设
,行列式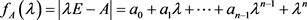 ,
,
称为矩阵
的特征多项式.
定理1.1 [2] :如果
阶矩阵
的特征多项式能够分解表示成不同一次因式方幂的乘积

其中
是
的相异的特征值,
是特征值
的重数,且
,则
的最小多项式具有如下形式
其中
求最小多项式
的步骤如下:
步骤1:找到矩阵
的特征多项式
步骤2:将特征多项式
化成标准分解式
步骤3:取包含一切不同因式幂积,按次数从低到高的顺序验证这些因式是否为
的零化多项式,其中使
零化的次数最低的幂积为矩阵
的最小多项式。
例题1.1:求矩阵
的最小多项式
解:矩阵
的特征多项式为
由定理1.1可知,矩阵
的最小多项式可能为:
,
,
因为
,
所以
的最小多项式为
3. 最小多项式的应用
3.1. 化简任意矩阵多项式
求解矩阵函数时,如果多项式次数较高,直接计算
会比较繁琐,而利用最小多项式可以降低
的次数,再将矩阵
带入求解,使运算达到了简化的目的。
利用最小多项式化简任意矩阵多项式的步骤如下:
步骤1:先求出矩阵
的最小多项式
步骤2:用
除
,得商式
和余式
,即
。
步骤3:由
且
可得
例题2.1:已知
,
,求
解:矩阵
的特征多项式为
矩阵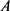 的最小多项式可能为:
的最小多项式可能为:
,
,
,
由于
,
,
因此矩阵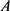 的最小多项式为
的最小多项式为
,
设
,
且通过计算可得

因此
。
3.2. 求线性空间的维数和一组基
在代数中一般通过线性空间的极大无关组表示线性空间的基,计算比较繁琐,利用最小多项式求线性空间的维数和一组基,可以使过程更加简便。
定理2.1 [3] :设
的全体多项式形成的线性空间是
,并且
是
的最小多项式,则有
1)
的维数等于
的次数
,即
;
2)
为
的一组。
例题2.2:矩阵
,其中
,
,其中
为
的特征多项式,求
的维数及其一组基。
解:矩阵
的特征多项式为
,
由于
,
,
则
有三个互异的特征值,矩阵
的最小多项式为
,
由于
,
因此
是矩阵
的全体多项式生成的线性空间
的一组基。
3.3. 求解矩阵方程
对于矩阵方程
的求解方法,通过矩阵的最小多项式来求得矩阵方程
的解,使方程的结果更加简洁。
定义2.1 [4] :设两个线性空间
、
,
是
到
的映射,
的定义域和值域分别记录为
和
,任取 ,若
,
,那么称
是以
为定义域的
到
的线性算子。
,若
,
,那么称
是以
为定义域的
到
的线性算子。
定理2.2 [5] :设
,若
、
是
在
到
的线性算子则有
,
。
定理2.3 [5] :由
可知,方程
与方程
等价。
定理2.4 [5] :
可逆的充要条件是
,
且
,
其中
为的
次数,
满足
。
例题2.3已知
,
,
,
求解矩阵方程
。
解:矩阵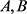 的最小多项式分别为
的最小多项式分别为
,
,
由于
,
取
,从而
,
将
,代入
,
得
。
3.4. 在矩阵对角化中的应用
利用最小多项式的相关理论得到矩阵能够对角化的一个充要条件,可以较快地判断矩阵能否对角化。
定理2.5 [6] :
阶矩阵
的最小多项式无重根的充分必要条件是矩阵
能够对角化。
例题2.4:判断在以下两种情况下矩阵
是否能够对角化。
1)
;2)
。
解:1)
,
为
的零化多项式,因为特征方程无重根,所以
能够对角化。
2)
,
为
的零化多项式,因为特征方程无重根,所以
能够对角化。
4. 结论
本文利用特征多项式的标准分解式,求矩阵的最小多项式。结合最小多项式的相关定理,概括了最小多项式的五种应用,包括:通过带余除法,降低多项式的次数,化简任意多项式;根据最小多项式的一些定理,更加简洁的得到线性空间的维数及其一组基;引用线性算子
、
,并利用 可逆的充要条件,求解矩阵方程
;通过判断矩阵的最小多项式有无重根来判断矩阵
能否对角化,并分别结合例题,列举了最小多项式在这四方面的具体应用。矩阵最小多项式的应用还可以推广到其他领域,因此对于矩阵最小多项式的应用还可以进一步研究。
可逆的充要条件,求解矩阵方程
;通过判断矩阵的最小多项式有无重根来判断矩阵
能否对角化,并分别结合例题,列举了最小多项式在这四方面的具体应用。矩阵最小多项式的应用还可以推广到其他领域,因此对于矩阵最小多项式的应用还可以进一步研究。