1. 引言
矮塔斜拉桥又称“部分斜拉桥”,是介于刚性连续梁桥和柔性常规斜拉桥的一种桥型,具有刚柔相济的结构特性 [1] [2] 。矮塔斜拉桥具有经济、美观、施工方便、跨径布置灵活等优点,近二十年来,在国内外城市景观桥梁、轻轨、高速铁路桥梁建设中得到广泛应用。矮塔斜拉桥在我国应用的历史仅十多年,在索力优化、受力特性研究、极限承载力分析、施工控制等诸多领域仍有待进一步的研究 [2] [3] [4] [5] 。
合理成桥状态是指斜拉桥在施工结束后,在所有恒载作用下,包含预应力荷载,各个构件受力满足某种理想状态。目前,进行一般斜拉桥成桥索力优化的方法主要有影响矩阵法、零阶方法、最小弯曲能量法等 [6] [7] [8] [9] 。但是混凝土矮塔斜拉桥主梁配置了大量体内预应力钢筋,体内预应力对成桥状态的影响与斜拉索索力分布状态作用相当,因此不能完全照搬斜拉桥一般索力优化的方法。必须考虑体内预应力作用影响与斜拉索索力比例分配优化问题,处理好索力和预应力同时优化的关系。目前的相关文献,对于同时考虑索力与预应力影响的方式比较模糊。
本文以常熟市碧溪大桥为工程背景,基于影响矩阵方法,考虑主梁体内预应力影响,以主梁和主塔单元的弯曲能量最小为目标函数,以主梁和主塔控制截面(如塔底截面、主梁根部截面等)的内力为约束条件,对大桥进行成桥索力优化。
2. 工程概况与模型的建立
常熟市碧溪大桥为双塔双索面混凝土矮塔斜拉桥,跨径布置41.6 + 80 + 41.6 m,桥面宽32 m。主塔下部为等截面、上部为变截面的现浇钢筋混凝土结构,从主梁顶面起主塔高为15.8 m;主梁为双向预应力双肋板式截面。主塔在桥台上部塔-梁-墩固接,副塔在塔梁固接梁底设立支座。每个桥塔斜拉索7对,由环氧喷涂钢绞线组成,标准强度1860 MPa。主桥立面图及拉索编号如图1所示。
本文借助于有限元软件MIDAS/CIVIL 2010对于大桥进行有限元仿真分析,主梁、索塔和桥墩以梁单元进行模拟,建模时采用“双主梁模型”。考虑到斜拉索只受拉并有一定的初张力,采用桁架单元对其进行模拟,拉索的垂度效应影响采用Ernst公式换算弹性模量。拉索锚固点均采用和主梁主塔单元共节点的方式进行模拟,塔墩梁固结处采用梁单元共节点方式处理,塔底固结处理。主梁按照截面积等效和抗弯刚度等效原则,双肋与中横梁以共节点的方式组成空间平面框架;主塔按照实际结构尺寸进行模拟。全桥计算模型共划分365个单元。全桥有限元模型如图2所示。

Figure 1. Main bridge elevation and cable number
图1. 主桥立面图及拉索编号

Figure 2. The overall finite element model of Bixi Bridge
图2. 碧溪大桥整体有限元模型
3. 成桥索力优化计算原理
影响矩阵法是基于调值计算原理提出的一种索力优化方法,它可以考虑主梁预应力及汽车活载等多种因素的影响,通过设置优化控制目标和约束条件,得到满足设计要求的合理成桥索力。本文采用影响矩阵调值原理,以大桥结构弯曲应变能为目标函数,考虑预应力及运营车辆荷载作用,以结构关键截面应力容许范围为约束条件,进行成桥索力优化。计算过程如下:
假设结构满足线性叠加原理,根据影响矩阵的定义:
(1)
其中
为施调相量索力向量;
为梁塔关键面弯矩向量;
为影响矩阵。
以大桥结构弯曲应变能为目标函数,则:
(2)
式中:m为离散结构的单元总数;
、
、
分别为i号单元的杆件长度、弹性模量、截面惯性矩;
、
分别表示单元i杆件左右端弯矩。上式矩阵形式为:
(3)
式中:
,
分别为杆件单元左右端弯矩向量;
为对角系数矩阵;
对角系数为:
令调索前杆件左右端弯矩为
、
,施调索力向量为
,则调索后弯矩向量
(4)
式中:
、
分别为索力对左右端弯矩的影响矩阵,将式代入式得:
(5)
为与
无关的常数,由结构特性及其他荷载效应决定。根据变分原理,为了使结构弯曲应变能最小,则
。n为调索的总数,即56。得到:
(6)
求解式线性方程组即可得到结构弯曲应变能最小目标下的成桥索力。
4. 成桥索力优化实施流程
采用MIDAS/CIVIL 2010“未知荷载系数”索力优化功能模块自动计算并根据结构分析经验进行局部人工调整,实现合理成桥索力。以主梁和主塔控制截面(如塔底截面、主梁根部截面等)的内力为约束条件,主梁主塔全部单元的上下缘应力为验算条件(必须满足),兼顾拉索力均匀性以及边墩反力,对大桥进行成桥索力优化。具体实现过程如下:
1) 根据设计资料,建立碧溪大桥空间有限元模型。
2) 确定各斜拉索张力荷载工况以及结构自重、预应力荷载、二期恒载等荷载工况。
3) 根据实际支承情况对有限元模型施加边界约束条件,进行一次落架成桥计算。
4) 利用“未知荷载系数”模块功能,选取弯矩应变能作为目标函数。约束条件为:索塔塔顶侧移以及主梁跨中挠度限值,索塔塔底与主梁固结处截面、主梁根部与索塔固结处截面、主梁边跨四分点截面以及主跨八分点截面弯矩限值;边墩不出现负反力。求解拉索初张力并组合荷载。
5) 判断主梁主塔的边缘应力是否超过材料容许应力,结构应力分布是否合理。否则重新调整“未知荷载系数”来调整索力。
6) 调整索力使主梁主塔的边缘应力、拉索索力相对均匀。将此荷载组合作用下的索力值作为合理成桥索力。
5. 成桥索力优化计算结果与分析
表1为一次成桥合理拉索初张力,在此组斜拉索初张力以及结构恒载作用下,进行一次落架计算,得出成桥状态下斜拉索内力即恒载作用下合理成桥索力,如表2所示。相应的成桥结构内力及应力状态如图3~7所示。
与合理成桥索力对应的合理成桥结构内力及应力状态如图3~7所示。

Table 1. Reasonable initial tension of integral cast construction
表1. 一次成桥合理初张力

Table 2. Reasonable bridge cable force
表2. 合理成桥索力

Figure 3. Reasonable bridge cable force histogram
图3. 合理成桥索力柱状图

Figure 4. Reasonable bridge bending moment diagram
图4. 合理成桥弯矩图

Figure 5. Reasonable bridge axial force diagram
图5. 合理成桥轴力图
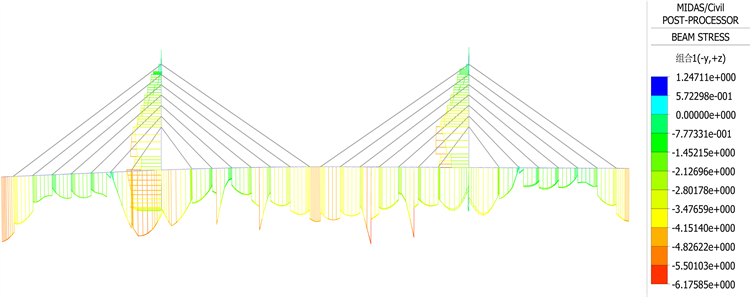
Figure 6. The upper edge stress diagram of a reasonable bridge structure
图6. 合理成桥结构上缘应力图

Figure 7. The lower edge stress diagram of a reasonable bridge structure
图7. 合理成桥结构下缘应力图
从图中可以看出,优化计算得到的大桥成桥索力比较均匀且有一定规律。与此相对的成桥结构内力状态,主梁和主塔弯矩幅值很小,主梁弯矩幅值最大6670 kN·m,最小−6322 kN·m。由于碧溪大桥跨径不是很大,该弯矩幅值比较小,且主梁弯矩图接近主梁形心连线分布。
主梁根部位置以小幅正弯矩为主,边跨L/2截面和主跨L/2截面弯矩分布都是小幅负弯矩为主,有利于减小运营期间混凝土收缩徐变和预应力损失对于结构的不利影响,增加了安全储备。
主梁轴力变化均匀,主梁主塔上下缘应力大小变化均匀。除了边墩附近主梁下缘应力有0.6 Mpa左右的拉应力外(远小于结构拉应力极限为1.89 Mpa),主梁主塔在其余区域全截面受压,应力幅值为−6.7 Mpa,结构具有足够的安全储备。
综上所述,此成桥车辆荷载作用下的结构内力分析表明,活载作用对结构内力影响较小,主要原因是混凝土矮塔斜拉桥恒载较大。斜拉索应力增量最大为39 Mpa,远小于斜拉索强度极限。
状态满足设计规范及成桥状态优化目标要求,该成桥状态下结构弯曲应变能接近最小,此组索力可以作为合理成桥索力。
6. 结语
以常熟碧溪大桥(矮塔混凝土斜拉桥)为工程背景,基于影响矩阵方法,在计入已知的主梁体内预应力的前提下,以主梁和主塔单元的弯曲能量最小为目标函数,以主梁和主塔控制截面(如塔底截面、主梁根部截面等)的内力容许范围为约束条件,对大桥进行了成桥索力优化分析。研究结果表明:
1) 优化分析得到的大桥成桥索力比较均匀且有一定规律。
2) 在边跨和中跨跨中位置弯矩分布以小幅负弯矩为主,主梁根部位置以小幅正弯矩为主,此种内力状态有利于减小混凝土收缩徐变和预应力损失给桥梁运营带来的不利影响。
3) 对成桥状态下进行了移动车辆荷载作用分析,结果表明活载作用对混凝土矮塔斜拉桥结构状态影响较小。
基金项目
江苏省自然科学基金项目(BK20160207)。
NOTES
*通讯作者。