1. 引言
近场声全息是近年来应用比较热门的一门技术,应用近场声全息技术能够反演出整个声场的参数。近场声全息技术在工业中应用最广泛的就是用来定位和识别噪声源。
1948年,Gabor在研究解决电子显微镜的球面像差问题时提出了全息技术原理,由于声波具有光波相似的传播特性,A. F. Metherell在20世纪60年代末期将光全息技术原理引入声学领域并首次提出了声全息的概念。本文着重回顾近场声全息技术的发展过程,学者们经过长期的研究从自由声场中近场声全息的应用到非自由声场中近场声全息的应用。非自由声场中近场声全息的应用更加贴近于工程实际,因为在实际工作中,噪声的污染是不可避免的,近场声全息在非自由声场中的应用使得其应用前景大大增强,但是如何在非自由场中分离声场从而虚拟出目标声源的自由场这是目前应用工作的一个难点。本文旨在通过回顾近场声全息的发展过程,梳理出近场声全息的一些关键技术点,并在最后指出近场声全息发展的方向。
2. 自由场中声源的重建
声源在自由场中辐射和传播声波服从亥姆霍兹微分方程的分布,学者们先后进行了正交共形结构的近场声全息研究和任意结构的近场声全息。
2.1. 正交共形结构近场声全息的研究现状
上世纪80年代初,Williams、Maynard和Veronesi (1985, 1987) [1] [2] [3] 提出近场声全息理论和算法,其测量平面到源面的距离是波长的几分之一,在测量系统的动态范围选择适当的情况下,可充分记录测量全息面上声场的低波数和高波数成份,因此,重建分辨率可以很高,它只与测量面和系统的动态范围之比有关。在NAH的算法中,利用测量面上的声压为源面上的声压与格林函数卷积关系,将二维傅里叶变换应用于Helmholtz方程,实现实空间域(Real-Space)到波数域(K-Space)的快速变换计算,可由声压测量重建源面声压场、振速场及声强场的分布以及远场指向性等声场量。平面共形结构近场声全息变换可以推广到其他正交共形结构近场声全息变换。Williams和Dardy (1987) [4] 首先将NAH推广到柱坐标系,提出了研究柱形声源声场重建的近场声全息(CNAH, Cylindrical Nearfield Acoustical Holography)的原理和方法。利用2D-FFT (The fast Fourier Transform)计算同轴的两柱面上声场的空间变换,讨论了k-space滤波和重建分辨率等问题,给出了离散声场的DFT (The Discrete Fourier Transform)算法,并进行了有限长柱的实验研究。Lee (1996) [5] 又将NAH推广到球坐标下球形声源的声场空间变换(SNAH, Spherical Near Field Acoustical Holography)。理论上讲,有多少种正交坐标系和相应的正交函数组,就可以导出相应的正交共形结构声场空间变换关系。Sarkissian在1990年 [6] 提出了用于分析轴对称声源的声全息技术,并在此基础上研究了用于分析有限振动体的NAH技术。
2.1.1. 测量孔径有限性影响的研究
声压测量只能在靠近振动体的一个有限的测量孔径上进行,测量孔径的有限性使得NAH在大型振动体如船体等上的大规模应用难以实现。Maynard等(1985) [2] 研究了测量孔径的有限所带来的一些问题,包括在声源表面振速重建过程中的wrap around误差等。通过在测量孔径周围填零形成保护带,形成远大于测量孔径的虚拟孔径,消除了wrap around错误。然而,填零后测量孔径边缘的非连续性会在NAH后向传播过程中放大,从而严重污染重建结果。为了避免这种非连续性,需要对补零后的全息面数据做平滑处理。传统的作法是对补零后的全息数据加一个合适的实空间窗函数。然而,在传统的加窗数据平滑过程中,在将测量孔径外的数据置零的同时,也改变了测量孔径内的数据,从而产生新的重建误差。目前,改善测量有限孔径对重建精度影响的主要途径是数据外推技术。数据外推是在保证测量孔径内的数据不受影响的同时,外推出测量孔径外的数据,以提高重建精度。与传统的加窗数据平滑方法相比,基于数据外推技术的数据平滑方法在外推测量孔径外的数据的同时,不会改变测量孔径内的全息面测量数据,因此,有效扩大了全息面孔径,而没有扭曲测量孔径的数据,有效减小了测量孔径有限性的影响。Saijyou和Yoshikawa (2001) [7] 对数据外推技术进行研究,提出real-space和k-space两种新的数据外推方法。Sarkissian (2004) [8] 也进行了类似的研究。
降低测量孔径对重建精度影响的另外一种途径是补丁(Patch) NAH技术。当只对振动体表面某部分的振动情况感兴趣时,为了重建振动体表面该部分处的法向振速,补丁NAH技术只需在靠近结构体该部分表面的共形面上进行声压测量即可,能以较小的代价完成大型结构的NAH分析。Williams等(2003) [9] 的研究工作表明,对于单点激励振动体的辐射声场,在距离0.4 cm的两个共形表面上,频率范围为200 Hz~2700 Hz的重建法向振速的根方差平均小于20%,并可重建出声强,重建误差小于30%。
2.1.2. 重建稳定性与可靠性研究
为了提高NAH的算法稳定性与可靠性及其抗噪声干扰的能力,在real-space或k-space普遍采用加窗滤波。Veronesi等(1987) [3] 提出一种后来被广泛应用的k-space滤波函数,其主要参数是截止频率,但是对测量面离源面距离非常敏感,随着距离的增大效果越来越差。Fleischer和Axelrad (1986) [10] 提出一种k-space的Weiner滤波窗函数,其主要参数是信噪比,形式比较简单。张德俊等(1992) [11] 提出一种最小二乘法k-space滤波窗函数,它与测量信噪比和测量距离及声源频率密切相关,对测量距离的适应性比较好,但在高低边带处的光滑性差。Li等(1994) [12] 通过改变约束条件,提出改进的最小二乘滤波函数,改善了窗函数在高、低边带的光滑性。
虽然在NAH变换中,可以通过滤波提高重建精度。但NAH测量中难免受到各种干扰。测量系统误差及各种环境干扰都将因格林函数的奇异性,在源面场的重建中被放大,而影响重建的效果。Garroll等(1999) [13] 和Nam及Kim (1999) [14] 对各种因素如背景噪声、测量面位置偏差、传感器位置偏差、传感器间的响应一致性偏差等在平面NAH中引起的重建误差进行系统分析,给出随机误差和测量参数间的定量关系,发现随机误差的影响远大于传声器位置偏差的影响,而且随机误差的影响在声压空间频谱的高波数域更加明显,并指出滤波技术是降低这种影响的最佳方法。
2.2. 任意形声源结构近场声全息
正交共形结构声全息变换最突出的优势是获得声场信息量丰富,并大多可借助于FFT快速计算,但最大的缺陷在于对重建的声源表面形状的适应性差。由于实际结构的形状各式各样,结构表面为正交坐标系的情况较少,所以仅靠正交共形近场声全息变换远远无法满足工程需求。当声源为任意几何形状时,需要一种更加通用的声场重建途径。解决该类问题的途径之一是通过数值求解Helmholtz积分方程,建立任意形结构的近场声全息理论。
2.2.1. 重建算法研究
Veronesi和Maynard (1989) [15] 提出用边界积分法实现任意形结构声源表面近场全息重建的原理与方法,利用常数单元法离散Helmholtz 积分方程获得了测量得到的声压和声源表面节点上的法向振速之间的矩阵关系,即所谓的辐射算子,通过对辐射算子求逆,获得法向振速分布。Bai (1992) [16] 对边界积分的声全息变换进行改进,引入边界元方法(BEM, The Boundary Element Method),提出基于BEM的任意结构近场声全息变换法(BEM based NAH)。其作法是将源面离散,利用离散后的表面和外部Helmholtz积分方程,建立源外部测量点上的复声压与源表面上各单元的法向振速的线性方程组。振动结构的几何形状及振动结构和测量全息面之间的振–声关系通过BEM描述为振–声传递矩阵。结构的表面振速分布可以通过对振–声传递矩阵求逆,由外部声压重建得到。再利用表面离散Helmholtz积分方程,由表面振速求出表面声压,从而实现源表面场的重建。
Kim和Ih (1996) [17] 及Kim和Kim (1999) [18] 采用了BEM based NAH重建非规则边界空腔内壁的法向振速分布。Williams等(2000) [19] 在涡轮螺旋桨飞机机身内壁的共形面上测量声压,采用BEM based NAH在螺旋推进器的叶片通过频率及其前两阶谐频处重建机身表面的法向振速分布,揭示出发动机噪声向机舱内的结构传播路径和空气传播路径。
处理任意形结构声源辐射问题的另外一种途径是等效源方法。这种方法的基本思想是采用一系列定位的基本源(即等效源),如单极子源和偶极子源等,代替真实声源。通过测量参数如声压、声速等,和由一系列等效源产生的合成值之间强加一个相容性(或协调性)条件,可以得到这些声源的理想分布。这种方法的优势之一是在大多数情况下,对声场建模需要的自由度数少,克服了BEM计算效率差的缺陷。Helmholtz积分方程最小均方误差法(HELS, Helmholtz Equation Least Squares) [20] 是等效源方法的一种典型方法。上世纪80年代中期,Chao (1987) [21] 利用早期关于声场的正交函数适配法,提出一种用于声场逆变换的基于正交函数适配的最小平方误差方法。它将声场近似表示成一组正交完备的函数组的线性组合,利用LMS (Least Mean Square)准则由测量点的声压数据求出展开式中的待定系数,从而可以确定声场中包括源面上的声压或振速分布。通常这种方法的展开项数或测量点数比基于BEM的任意形结构声场全息变换法中源面离散点数或外部测量点数少很多,并且避免了大量耗时的积分运算,计算量远小于BEM变换法,从原理上讲该方法适用于任意形结构声源的声场重建,后来Wang和Wu (1997) [20] 称这种方法为HELS法,并选取球函数为基本函数,进行了各种参数变化对重建效果影响的分析,但存在对长形振源重建计算收敛性差的问题。HELS法在实施过程中关键是根据声源形状,选取合适的收敛快的正交函数组以及合适的外部场点。同时,M. Villot等(1992) [22] 和Wu等(1998) [23] 还将该方法推广应用到结构内部声场的声全息重建中,这里分别采用了球函数和三角函数作为基本函数。Wu等(2002) [24] 将HELS法和BEM法结合起来用于实现任意形结构声源的全息重建。该方法兼具HELS方法和BEM方法的优点:输入数据的大部分来自于修正HELS构造而非测量得到,因此声场重建的效率非常高;同时,声场重建精度由Helmholtz积分方程和修正的Tikhonov正则化方法及GCV方法保证,使得HELS方法可以在测量面上快速收敛。
毕传兴等(2003) [25] 在边界元法研究的基础上,提出基于分布源边界点法的声场重建和预测技术。它继承了BEM的优点,不受具体形状的限制,同时又有效地避开了系数矩阵的直接计算和具体的插值,也不用进行数值求积和奇异积分的处理。考虑到重建求逆过程对实际测量误差具有放大的负作用,文中在重建过程中采用Tikhonov正则化处理,选择合适的正则化系数,滤去传递矩阵的奇异值分解中对重建结果贡献小且对误差异常敏感的项,从而进一步优化重建结果,保证重建结果的有效性。
商德江(1994) [26] 对任意形结构非共形面全息场变换进行了计算模拟和精度分析,指出在平面–球面、双平面–球面非共形变换及球面–球面共形变换中,单平面–球面变换偏差最大,双平面–球面变换偏差和球面–球面共形变换偏差几乎相等,可作为声场逆问题、空间场重建应用;文中设计了双水听器声场扫描测量装置,既可做双水听器声强测量,又可做全息场测量和场重建的实验研究,并用此装置进行了球形声源的双平面全息变换实验研究;文中对任意形结构非共形面声场变换在源定位中的应用进行了研究。暴雪梅和何祚镛(1997) [27] 将NAH方法应用于水下散射问题研究。文中由散射体近场全息面上的复声压数据重建散射体表面的散射场,并进一步预报远场散射声指向性。
2.2.2. 积分的奇异性和解的非唯一性问题研究
采用BEM离散Helmholtz积分方程是进行任意形结构声源重建最流行的方法。其主要优势在于对声源几何形状适应性强,但同时也增加了计算量,因为离散后的矩阵通常都是非对称的满阵。除此之外,还产生了奇异积分的问题,无论是否需要获得满意的精度,都需要巧妙的积分技术,如极坐标变换法等,从而增加了额外的计算量。Gardner B. K.和Bernhard R. J. (1988) [28] 研究了在声源边界造成的谐振腔特征频率上产生的解不唯一性问题。较有代表性的解决办法有Schenck (1968) [29] 提出的CHIEF (Combined Helmholtz Integral Equation Formulation)法和Buton与Miller (1971) [30] 提出的Buton & Miller法,CHIEF的主要思想是增加声源表面内部少量点上的信息,以获得该问题的超定解,从而获得唯一解;Buton & Miller法通过建立Helmholtz积分方程及其法向导数的线性组合获得唯一解。这些方法都会增加计算量。而且CHIEF法难以选择有效的CHIEF点,Buton & Miller法在法向求导时会产生超奇异积分,增加了处理的难度。
2.2.3. 重建过程中病态问题研究
对于BEM based NAH方法,重建方程可以视为一个线性方程p = Gv,p是测量得到的声压,v是未知的振动结构表面上的法向速度,G是一个已知传递函数。通过对此方程求逆,可得到声源表面振速。由于剧烈衰减的瞬逝波成份的存在,该方程病态性严重,声压p小的改变通常会导致v的大的变化。实际测量时,测量声压的幅值和相位都会存在一定误差,如果直接采用对传递矩阵进行求逆来重建,这些误差会成倍地放大,重建得到的表面法向振速往往会存在很大的误差。因此,减小测量误差的影响,是保证重建结果及应用此结果进行声场预测的精度的关键。
解决声场重建病态性的传统方法是奇异值分解(SVD, The Singular Value Decomposition)滤波技术 [31] 。该技术对振–声传递矩阵进行SVD,并截断小奇异值, 即低空间波数滤波,从而改善重建效果。但这种方法存在很多问题,如截断次序无法正确选择、截断阈值不好确定等,在SVD滤波技术的基础上,发展出控制逆问题中误差影响更有效的方法即正则化方法。正则化处理的基本思想实际上是采取滤波方式来控制传递矩阵的SVD各项中对重建结果贡献小而又对误差非常敏感的各项的影响。
现在BEM based NAH技术中应用的正则化方法主要有,标准Tikhonov正则化(The Standard Tikhonov Regularization Procedure)、修正Tikhonov正则化(The Improved Tikhonov Regularization Procedure)、Landweber迭代正则化(Landweber Iteration Regularization Approach),共轭梯度正则化(The Conjugate Gradient Regularization Approach)。所有这些正则化方法都包含一个不确定的参数–正则化参数,该参数本质上为k-space滤波器的断点,控制着重建表面法向振速对误差扰动的敏感度,因而准确地选取正则化参数也是影响重建结果的一个关键,如果正则化参数选择不当,要么难以起到滤波的作用,要么会丢失大量有用的信息。它必须通过独立的方法确定,参数选择方法 [32] [33] 分为两类,一类依赖于噪声方差的先验知识,另一类无须先验知识。其中,前者的代表方法是离差原理方法(MDP, The Morozov Discrepancy Principle),而后者的代表方法是L曲线法则(L-Curve)、广义交叉验证函数法(GCV, The Generalized Cross Validation)。
目前,关于正则化过程在NAH中的应用的研究工作主要有:Kim和Ih (1996) [17] 首先将Tikhonov正则化方法用于内部NAH问题,Nelson和Yoon (2000, 2000) [34] [35] 研究了GCV方法在NAH的Tikhonov正则化过程如何确定正则化参数。Kim和Ih (2000) [36] 提出使用Landweber迭代正则化方法进行正则化处理,为了获得最优迭代步步数,需要进行最小平均方差估计。文中设计了最优波向量滤波(Optimal Wave Vector Filter)曲线,以除去会产生较大重建误差的高阶模态。大障板辐射体的实验结果表明,与没有使用任何正则化处理相比,应用这种正则化过程可以降低重建误差48%,与使用最优截断正则化处理相比,这种新的技术可以多降低重建误差7%~39%。Williams (2001) [37] 集中讨论了各种正则化方法在平面、圆柱面、球面及其他各种共形面的内部和外部NAH中的应用。为了在这些正交几何问题中应用正则化理论,文中重新整理了平面、圆柱面和球面NAH重建方程,将之变为特征值问题,可以很容易地与正则化理论结合。文中就各种正则化方法的重建精度进行了比较,在此基础上提出一种修正Tikhonov正则化方法,研究表明该方法优于其他正则化方法。为了选择正则化方法的最佳参数,文中对需要先验知识–噪声方差的正则化参数选择方法MDP和无须任何先验知识的正则化参数选择方法GCV进行了研究并对比,认为GCV方法比MDP更有优势。徐张明等(2002) [38] 较为深入地研究了L-curve方法在Tikhonov正则化过程中的应用及应注意的工作。
3. 非自由场中声源的重建
美国的David L. Schoch和Maqsood A. Mohd博士在户外开放空间中,首次进行了虚拟消声室可行性研究。他们的目的是想为美国空军开发测试中心研究开发一个户外测试场(An Open Air Test Arena,简称OATA),解决被测航天飞行器由于体积过大无法在消声室中进行电磁适配性(Electromagnetic Compatibility,简称EMC)和电磁干扰(Electromagnetic Interference,简称EMI)测试的问题。2007年,英国的Grant MacLean进行了在野外跟踪动物用的三维微型GPS (Global Position System,全球定位系统)接收天线性能测试的研究,主要是用来解决在消声室内不能接收GPS远场信号的难题。建立E3测试所需虚拟消声方法要解决的关键科学问题为:如何在户外测试场通过设计调整天线阵列和滤波器避开或消除电磁干扰的路径、频率分量和反射。
对于声波分离这一虚拟消声方法的关键科学问题,在海洋声学、气动声学和结构声学等领域都有专家在研究。基本理论依据是:声场很显然有无限维的自由度,那么就可以充分利用场动力学的知识将声场参数化,而不是通过设法测量声场中每一处的声学量来了解声场。以声压作为声场中最基本的声学量,它是由波动方程约束的解,可以表达为一系列扩展的、相互正交和已知其空间形态的基函数的叠加。这些基函数分别表达不同方向、不同波数的声波。因此,对声场的知识和了解就转化为对基函数的系数的知识和了解。这样一来,声场分离的研究焦点成为:如何在声场中布置声压传感器的空间位置,以及如何利用声压测量值求解基函数的复系数,最后达到声场分离和重构的目的。
而在结构声学领域,有两类较为典型的声场分离方法。第一种方法为:在声场中布置两层平行且同形的、规则的全息声压测量面,如将麦克风阵列布置成平面、柱面或球型面,然后利用两个全息面上的声压测量值以及两个全息面上基函数的正交性,来求解和分离出声场中两类不同的声波。1956年,Pachner首次提出使用两个不同半径的同心球型全息测量面,求解和分离声场中的行波和驻波。1980年,Weinreich和Arnold同样使用了两个半径分别为58.1 cm和72.6 cm的同心球型全息测量面,来分离和重构在小全息面内的声源和在大全息面外的声源,试验设置见图1,图中O为坐标原点;M1,M2为麦克风;A为扫描天顶角θ的电机;B为扫描方位角φ的电机。
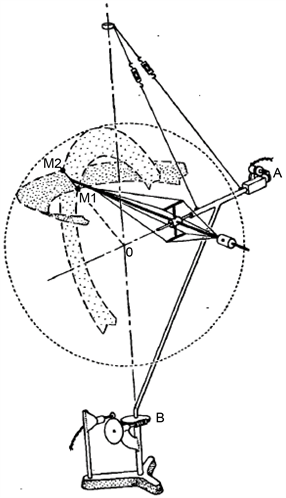
Figure 1. Double holographic spherical sound pressure mechanical scanning system
图1. 双全息球面声压机械扫描系统
上个世纪80年代以来,由于学者们对近场声全息研究的重视,以各种近场声全息技术为基础的对声场分离的研究又重新受到重视。如Jacobsen [39] Cheng,Mann和Pate使用了两个同轴的近场圆柱全息测量面,来分离一个散射器和一个活塞形成的声场,试验设置见图2,图中r1为第一全息测量面;r2为第二全息测量面;r0为声场分离面。
不像Pachner、Weinreich和李卫兵等使用球波函数作为基函数,以及Cheng、Mann和Pate使用柱波函数作为基函数表达声场的声压,C. X. Bi、X. Z. Chen 和J. Chen使用系列等效声源法 [40] 表达声场的声压,在近场布置了两个间隔7.5 cm的平行全息平面来分离和重构位于全息面两侧的两个喇叭辐射的声场,试验设置见图3,图中S1,S2为全息测量面;S*1,S*2为等效源面。
以上所提到的各位学者研究的声场分离方法,都是使用两个间隙很近的、同型的全息测量面。如果声源的结构足够大,如飞机和潜艇等,精确布置两层平行的、具有共型规则的几何形状的传感器阵列将是一项耗时、成本高和难以实施的巨大工程。2007年,Finn Jacobsen和Virginie Jaud提出了只用一个全息测量面的声场分离方法 [41] 。为了识别和分离全息面两侧的声源,在全息面的每个测量点上必须同时测量声压和空气粒子速度。图4为试验设置示意图,图中Measurement plane为全息测量面;Sound source1&2为声源。
虽然Finn Jacobsen和Virginie Jaud提出的声场分离方法 [42] ,只使用一个全息测量面,但是需要在所有测点上逐点扫描测量声压和空气粒子速度。由于空气粒子速度是矢量,它的测量远比声压这一标量的测量难度大、耗时且成本高。后来,国内张小正 [43] 也进行过类似研究。
2007年,国内学者李卫兵 [44] 、廉美转、毕传兴 [45] [46] 、陈剑和陈心昭 [47] 张海滨 [48] 也发表了同

Figure 2. Double holographic cylindrical sound pressure measurement system
图2. 双全息柱面声压测量系统
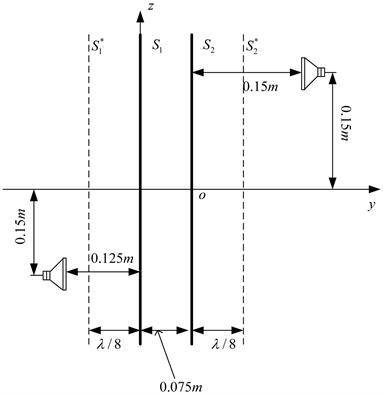
Figure 3. Double parallel holographic surface and sound source location
图3. 双平行全息面和声源位置
Weinreich和Arnold的研究方法相似的、分离由刚性散射球源和点声源组成的声场的仿真计算结果。
4. 结论
近场声全息技术充分利用了声源辐射出的倏逝波,从而在重构声源时非常精确。文章回顾了近场声
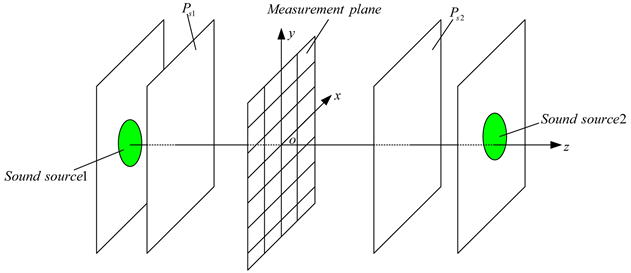
Figure 4. The location of the single holography and the sound sources
图4. 单全息面和声源位置
全息的发展过程,按照声源的形状可以建立不同的坐标系,在实际工作中按照声源的形状分为正交共性结构声源和任意性结构声源,其中对于正交共形结构声源采用最多的是快速傅里叶变换方法,但是在实际的重建工作中会受到测量孔径的影响和重建稳定性的影响。学者们研究了这两种影响的因素,也提出了减小影响的对策。对任意形结构的声源,重建的方法主要是边界元方法和等效源方法,但是在计算过程中都会遇到矩阵病态的问题,针对重建过程中的病态问题,学者们又做出了很多研究来减小重建的误差。非自由场中近场声全息的应用把近场声全息向工程实际的应用更加推进了一步,通过在非自由场中应用近场声全息不仅能把目标声源场和噪声源场分离开,而且能分别重建目标声源和噪声源。
5. 近场声全息技术的发展方向
由于球面具有非常好的对称性,其作为声压或者空气粒子振速的接收阵列具有很大的优势。近场声全息技术在声波的中低频段对噪声源的定位和识别比较精确,波束形成方法在声波的中高频段对噪声源的定位和识别比较精确。将两种技术结合起来能对全频段的噪声源进行比较精确的识别和定位。可以建立一种自适应算法,在中低频段自动采用近场声全息的方法定位和识别噪声源,在高频段自动采用波束形成算法来定位和识别噪声源,这两种技术的结合将是以后近场声全息技术发展的方向。