一种非最小耦合暗能量模型的研究

Study on a Kind of Non-Minimal Coupling Dark Energy Models

摘要: 本文研究的是一种非最小耦合暗能量模型。在这种暗能量模型中，作为暗能量的标量场与引力的耦合形式为F(∅)=1+α∅²。我们研究了该暗能量场的特征和演化行为，并分析了选取不同的参数对模型的影响。通过分析，发现参数α对模型的演化有关键性的作用——暗能量是否一直表现为Quintessence场。

Abstract: This paper studies a kind of non-minimum coupling dark energy models. In the dark energy models, the coupling form of the dark energy as a scalar field and gravity is  F(∅)=1+α∅². We studied the characteristics and evolution behavior of the dark energy field, and analyzed the influence of different parameters on the models. Through analysis, it is found that the parameter α plays a key role in the evolution of the model—whether the dark energy always appears as a Quintessence field.

1. 引言

目前的天文观测数据，如超新星、哈勃、Planck等，对一种具有负压特征的物质：暗能量提供了支持和限制 [1] - [8] 。暗能量和物质、辐射一样，都是宇宙的构成成分之一。并且，伴随着宇宙的膨胀，辐射和物质将在此过程中被稀释，从而在辐射和物质相继占主导地位之后，暗能量最终在宇宙演化中成为主要成分，并最终主导了宇宙的演化。因此，对于暗能量的研究就有了重要的意义。暗能量模型有很多，在本文中，我们研究的是与引力有非最小耦合的标量场暗能量模型。在这类模型中，因为暗能量与引力有非最小耦合作用 [9] - [13] ，而引起了有别于一般传统暗能量模型的演化情况。我们首先分析了一般形式的暗能量模型；然后又选取了一种具体形式为 $F\left(\varphi \right)=1+a{\varphi }^2$ 的耦合形式，与一种指数势能；最后分析了不同的耦合系数对暗能量演化的影响。

2. 一般形式的非最小耦合暗能量模型

对于一般的暗能量场 $\varphi$ 和引力发生非最小耦合的情况，普遍的拉氏量形式为 [9] ：

$L=\frac{F\left(\varphi \right)R}{16\text{π}G}+\frac{1}{2}k\left(\varphi \right){\nabla }_{\mu }\varphi {\nabla }^{\mu }\varphi -V\left(\varphi \right)+L_m$ (1)

因此，与之相对应的作用量为：

$S={{\displaystyle \int }}^{\text{}}{\text{d}}^{4}x\sqrt{-g}\left[\frac{F\left(\varphi \right)R}{16\text{π}G}+\frac{1}{2}k\left(\varphi \right){\nabla }_{\mu }\varphi {\nabla }^{\mu }\varphi -V\left(\varphi \right)+L_m\right]$ (2)

由(1)可得标量场 $\varphi$ 的运动学方程为：

${\nabla }_{\mu }{\nabla }^{\mu }\varphi =-\frac{1}{k\left(\varphi \right)}\left[\frac{-F^{\prime }\left(\varphi \right)R}{16\text{π}G}+\frac{1}{2}{k}^{\prime }\left(\varphi \right){\nabla }_{\mu }\varphi {\nabla }^{\mu }\varphi +V^{\prime }\left(\varphi \right)\right]$ (3)

其中的“'”代表对标量场 $\varphi$ 求导。

从(2)中可得：

$\frac{F\left(\varphi \right)}{16\text{π}G}\left(R^{\mu \nu }-\frac{1}{2}{g}^{\mu \upsilon }R\right)=-\frac{1}{2}{T}_m^{\mu \nu }-\frac{1}{2}{T}_{\varphi }^{\mu \nu }+\frac{1}{16\text{π}G}\left[{\nabla }_{\mu }{\nabla }^{\mu }F\left(\varphi \right)g^{\mu \upsilon }-F{\left(\varphi \right)}^{;\mu ;\nu }\right]$ (4)

$T_m^{\mu \nu }$ 为物质和辐射的能动量张量， $T_{\varphi }^{\mu \nu }$ 表示暗能量的能动量张量，即：

$T_{\varphi }^{\mu \nu }=k\left(\varphi \right)\left({\nabla }^{\mu }\varphi {\nabla }^{\nu }\varphi -\frac{1}{2}{g}^{\mu \nu }{\nabla }_{\mu }\varphi {\nabla }^{\mu }\varphi \right)+V\left(\varphi \right)g^{\mu \upsilon }$

由方程(4)，得：

$R=8\text{π}G\frac{-k\left(\varphi \right){\nabla }_{\mu }\varphi {\nabla }^{\mu }\varphi +4V\left(\varphi \right)+{\rho }_m-3P_m-3{\nabla }_{\mu }{\nabla }^{\mu }F\left(\varphi \right)}{F\left(\varphi \right)}$ (5)

把(5)代入前面的运动学方程(3)中，最后可得运动学方程：

$\begin{array}{l}{\nabla }_{\mu }{\nabla }^{\mu }\varphi =-\frac{1}{k\left(\varphi \right)}[\frac{-F^{\prime }\left(\varphi \right)\left(8\text{π}G\frac{-k\left(\varphi \right){\nabla }_{\mu }\varphi {\nabla }^{\mu }\varphi +4V\left(\varphi \right)+{\rho }_m-3P_m-3{\nabla }_{\mu }{\nabla }^{\mu }F\left(\varphi \right)}{F\left(\varphi \right)}\right)}{16\text{π}G}\\ \begin{array}{c}\underset{}{\overset{}{}}\\ \\ \end{array}+\frac{1}{2}{k}^{\prime }\left(\varphi \right){\nabla }_{\mu }\varphi {\nabla }^{\mu }\varphi +V^{\prime }\left(\varphi \right)]\end{array}$ (6)

公式(6)决定了 $\varphi$ 的演化。

3. 具体形式为 $F\left(\varphi \right)=1+a{\varphi }^2$ ， $K\left(\varphi \right)=1$ 的暗能量模型

以上的推导是适用于一般的非最小耦合暗能量模型的。我们下面具体分析一种 $F\left(\varphi \right)=1+a{\varphi }^2$ ， $K\left(\varphi \right)=1$ 的模型 [13] ，并采用势能 $V=m{\text{e}}^{b{\varphi }^2}$ ，分析它的特征。

在这种情况下，公式(2)的形式成为：

$S={{\displaystyle \int }}^{\text{}}{\text{d}}^{4}x\sqrt{-g}\left[\frac{1+a{\varphi }^{2}R}{16\text{π}G}+\frac{1}{2}{\nabla }_{\mu }\varphi {\nabla }^{\mu }\varphi -V\left(\varphi \right)+L_m\right]$ (7)

这种模型的暗能量能量密度为 [12] ：

$\rho =\frac{\stackrel{\dot{}}{\varphi }}{2}+3a{H}^2{\varphi }^2+V\left(\varphi \right)-6aH\varphi \stackrel{\dot{}}{\varphi }$ (8)

压强为：

$P=\frac{\stackrel{\dot{}}{\varphi }}{2}-a\left(2\stackrel{\dot{}}{H}+3H^2\right){\varphi }^2-V\left(\varphi \right)-4aH\varphi \stackrel{\dot{}}{\varphi }-2a\varphi \ddot{\varphi }-2a{\stackrel{\dot{}}{\varphi }}^2$ (9)

暗能量的状态方程为：

$w_{DE}=\frac{P_{DE}}{{\rho }_{DE}}=\frac{\frac{\stackrel{\dot{}}{\varphi }}{2}-a\left(2\stackrel{\dot{}}{H}+3H^2\right){\varphi }^2-V\left(\varphi \right)-4aH\varphi \stackrel{\dot{}}{\varphi }-2a\varphi \ddot{\varphi }-2a{\stackrel{\dot{}}{\varphi }}^2}{\frac{\stackrel{\dot{}}{\varphi }}{2}+3a{H}^2{\varphi }^2+V\left(\varphi \right)-6aH\varphi \stackrel{\dot{}}{\varphi }}$ (10)

4. 模型演化两种不同情况的分析

根据前面的运动学方程(6)，对暗能量场的演化进行数值计算。为了分析耦合系数a的作用，下面的分析选取同一种势能 $V=m{\text{e}}^{b{\varphi }^2}$ ，不同的耦合系数 $\left(a=\pm 0.01\right)$ 的两种情况。

1) 耦合系数a > 0

根据由于物质和辐射所占的比例为：

${\text{Ω}}_m=\frac{{\rho }_{matt}+{\rho }_{rad}}{\frac{{\omega }_0{\stackrel{\dot{}}{\varphi }}^2}{\varphi }+V\left(\varphi \right)-3H\stackrel{\dot{}}{\varphi }+{\rho }_{matt}+{\rho }_{rad}}\approx 30\%$

为了符合目前的实验数据限制，选取适当的初始条件，并用自然单位制，a = 0.01，m = 6，b = 0.1，使得今天 ${\Omega }_m=30\%$ ，如图1所示。

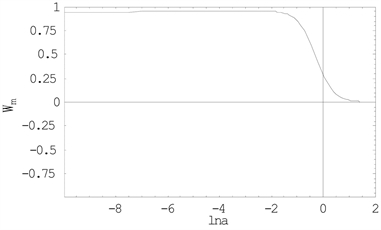
Figure 1. Percentage of matter and radiation

图1. 物质与辐射占的百分比

在这样的初始条件下，标量场的演化过程为：

图2横坐标为lna，纵坐标为标量场的值。标量场随时间越来越小，势能也随之减小，意味着这种情况下的暗能量场的状态方程一直大于−1，近似于比较普遍的一般暗能量场的行为。

Figure 2. The evolution of $\varphi$

图2. $\varphi$ 的演化过程

图3表示暗能量的状态方程w先是跟随辐射，然后跟随物质，最后下降到−1附近，最终状态类似于宇宙学常数。

Figure 3. The state equation w of the dark energy

图3. 暗能量的状态方程参数w

2) 耦合系数a < 0

如果使耦合系数a = −0.01；要使今天的 ${\Omega }_m$ 仍然为30%，如图4。

Figure 4. Percentage of matter and radiation

图4. 物质与辐射占的百分比

需要使m = 7；b = 0.1。

图5中，暗能量场随时间增加，因此势能和能量密度也随宇宙的膨胀而增加。这意味着它的演化过程与前面a = 0.01的情况完全不同。在某个阶段，表现形式类似于phantom场。

Figure 5. The evolution of $\varphi$

图5. $\varphi$ 的演化过程

图6是暗能量本身的状态参数w随时间的演化情况，在今天附近，它演化到了−1以下，跟图5暗示的情况是符合的。

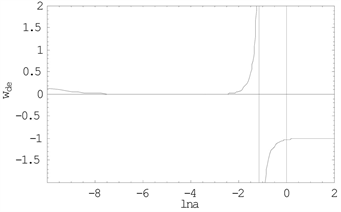
Figure 6. The state equation w of the dark energy

图6. 暗能量的状态方程参数w

可以看出，当a取正数时，暗能量场的演化行为先跟随物质和辐射；当物质和辐射被稀释后，暗能量场摆脱前两者的影响，逐渐接近于−1。而当a取负数时，在物质和辐射占比例大时，与a取正数的情况近似；物质与辐射比例变得足够小后，有一种先增加再减小到−1以下的过程。

以上a取正数或负数而导致的两种情况，都在目前的实验允许范围之内 [1] - [8] ，有待于观测的进一步精确。

5. 结论

根据前面的分析，这种非最小耦合暗能量模型的演化过程高度依赖于耦合系数a的选取，如果a大于0，演化情况类似于quintessence暗能量模型；而a小于0，则会有一个从quintessence场演化到phantom场的过程，最后状态方程参数w从下方无限接近于−1。这两种完全不同的情况给模型的演化提供了多种可能，提高了这类模型的普适性。