1. 引言
对流扩散方程 [1] [2] [3] 是一种常见的用来描述海洋、大气等环境和化学中传热、质量输运的等运动现象。众所周知,对流占优导致对流扩散方程呈双曲特性,采用标准有限差分法会导致数值震荡和数值弥散。为有效抑制数值震荡和数值弥散现象,国内外学者提出了求解对流扩散方程的迎风 [4] [5] [6] 和特征格式。Douglas [2] 利用二次Lagrange线性插值和差分法,提出了二阶修正特征线法(MMOC)法,并给出了收敛性分析。为改进二次Lagrange插值带来的数值震荡,陆金甫 [7] 、由同顺 [8] 和张鲁明 [9] 等人分别对特征差分法进行了修正和改进。由于MMOC特征差分不守恒,Douglas [10] 提出了修正对流的质量守恒的MMOCAA差分格式,芮红兴 [11] 提出了质量守恒的特征有限元格式,梁栋 [12] 提出了守恒的高精度质量守恒的特征差分法。
考虑到实际研究问题的规模大,计算时间长和计算存储量大的问题,算子分裂和区域分解算法 [13] [14] 被广泛应用到求解抛物型问题中。算子分裂把一个高维问题分解成多个一维问题,进而可以把一个十分复杂且包含多个变量的方程转化为包含一个或者较少的自变量的多个方程组。柳忠伟 [15] 结合LOD算子分裂、特征差分法和二阶本质非振荡法求解对流方程,但此算法不满足质量守恒。
结合算子分裂,二阶本质非震荡和质量校正法,本文提出了求解对流扩散方程的守恒特征法。在每个时间步,算法分三步,第一步,利用LOD算子分裂将方程分解成沿x方向和y方向的两个一维的偏微分方程组。第二步,在每个方向上,结合二阶本质非振荡和特征差分法,构造特征差分法。第三步,引入保守的MMOCAA格式,提出本质非振荡守恒特征差分格式。最后,通过数值实验验证格式质量守恒。
2. 模型
2.1. 对流扩散方程
对于伴有物质输运、气溶胶运动和分子扩散的物理过程以及粘性流体的流动等流体运动现象,都可用如下的数学模型表述。
(2.1)
其中有限区域
是流体的浓度,
为区域的边界,其中D,
分别表示扩散系数和速度场,不失一般性,假设它们均是常数,即
。
2.2. LOD算子分裂
局部一维格式
利用LOD算子分裂,将对流扩散方程分别沿x方向和y方向进行分解,得到如下的方程组:
(2.2)
分裂后的两个一维偏微分方程,若利用时间一阶格式和空间二阶修正迎风格式离散,截断误差可以达到
,且每个方向的方程可用追赶法求解。考虑到二阶修正迎风格式尽管可避免数值震荡,但在一定程度上带来了数值弥散,尤其在高对流占优扩散问题时,弥散现象变得更加明显。接下来,将结合特征差分和二阶本质非震荡法,解决对流扩散问题。
3. 算法
为了有效解决对流占优问题,第一步,分别对每个方向的方程采用特征线法处理,构造本质非振荡特征差分格式;第二步,加入质量校正项,引入保守的MMOCAA格式,得到校正后的本质非振荡守恒特征差分格式,并表示为矩阵形式;第三步,对于方程右端的未知项用本质非振荡插值求解,使其转化为已知项;第四步,利用追赶法 [16] 求解对角占优的三对角矩阵。
3.1. 特征线法
Step 1:沿x方向
(3.1)
采用特征线法
(3.2)
为x方向特征线,
和
分别为特征线与x和t方向的夹角,则
代入(3.2)得
方程两边同乘
,代入(3.2)式,得
离散上式,得
(3.3)
表示
的数值解,
将在后面给出。
Step 2:沿y方向
令
其中
是y方向的特征线,
,
分别为特征线与y,t方向夹角,离散化,得
其中,
表示
的数值解,
将在后面给出。而此时数值格式质量不守恒。
为解决格式质量不守恒问题,结合MMOCAA格式,现提出守恒的特征差分格式。
(1-a) 沿x方向,令
不失一般性,我们假定
,即点
落在
和
之间。
(1-b) 引入三个质量通量:
时的初始质量通量
中间质量通量
改进的质量通量
其中,
,
,
,
且
。
(1-c) 质量扰动参数
的确定
如果
,在这个时间步长内,误差是允许接收的。当
时,
被确定为
(1-d) 定义
它是容易验证格式沿x方向满足质量守恒
(1-e) 计算
。
加入质量校正后,(3.3)式变成
(3.4)
两边同乘
,令
则
化简得
(3.5)
记为
其中系数矩
因为
,所以系数矩阵A是一个严格对角占优的三对角矩阵。
(2-a) 沿y方向,
假定
。
(2-b) 质量通量。
时的质量通量
中间质量通量
改进的质量通量
其中,
,
其中,
。
(2-c)
的确定
如果
,误差可以接收。
当
时,
被确定为
(2-d) 计算
。定义
满足
(3.4)式加入质量校正后,得
(3.6)
令
,得
(3.7)
表示成矩阵形式,即
由于A,B均为严格对角占优三对角矩阵,故采用追赶法求解。
3.2. 本质非振荡插值
本部分给出
的计算方法。为了避免数值震荡,欲通过比较两个二阶差商的绝对值,选择绝对值相对较小的方法给出(文献 [8] )。
1) 当
为正数时,
(1-1) 当
时,利用牛顿插值得
(3.8)
同理
令
由上式计算可得,当
时,
当
时,
当
时,
,
时,
。
(1-2) 当
时,得
(3.9)
由上式计算可得,当
时,
当
时,
当
时,
当
时,
2) 当
为负数时,利用牛顿插值,
,
,
,
(2-1)
时,得
由上式计算可得,当
时,
当
时,
当
时,
,
时,
(2-2)
时,得
计算可得,当
时,
当
时,
当
时,
,
时,
。
同理,可得沿y方向。
4. 数值实验
方程(1)中的速度场系数
,扩散系数
,有限区域
,时间剖分
和空间剖分
。假定有初始时刻浓度只在
,
,
和
位置为1,其他位置浓度值为0。假定右端项
。
图1~图6展示了浓度在不同时刻的表面图和等值线图,由于对流项的存在,浓度会随着时间,沿着对角线方向行进,同时,由于扩散项的存在,浓度会不断的减小,这与物理现象相吻合。因此,我们的格式可很好地描述对流扩散问题,而且我们空间步长比较大时(
),没有出现数值震荡问题。
验证格式的质量误差,令时间剖分
和空间步长分别取
。并与文献 [15] 进行比较。

Figure 1. T = 0.0 s time concentration surface map and contour map
图1. T = 0.0 s时刻浓度表面图和等值线图

Figure 2. T = 0.1 s time concentration surface map and contour map
图2. T = 0.1 s时刻浓度表面图和等值线图
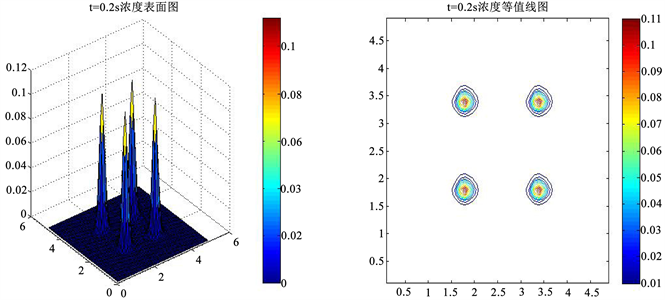
Figure 3. T = 0.2 s time concentration surface map and contour map
图3. T = 0.2 s时刻浓度表面图和等值线图

Figure 4. T = 0.5 s time concentration surface map and contour map
图4. T = 0.5 s时刻浓度表面图和等值线图
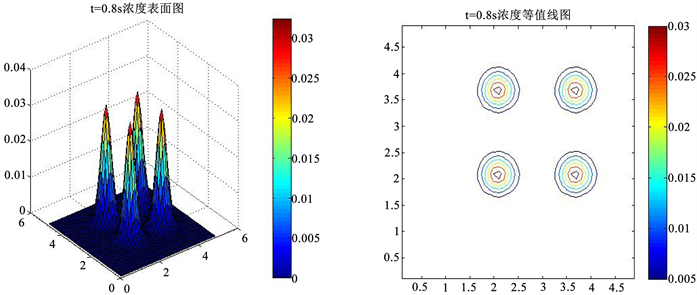
Figure 5. T = 0.8 s time concentration surface map and contour map
图5. T = 0.8 s时刻浓度表面图和等值线图

Figure 6. T = 1.0 s time concentration surface map and contour map
图6. T = 1.0 s时刻浓度表面图和等值线图

Table 1. Mass errors at the different time
表1. 不同时刻的质量误差
由表1中数据,可知在加入质量校正前,格式质量之差数值比较大,当加入质量校正后,格式质量之差可以达到
,可以认为是质量守恒的。
基金项目
国家自然科学基金资助项目(61703250, 61503227),山东自然科学基金资助项目(ZR2017BA029, ZR2017BF002)。
NOTES
*通讯作者。