1. 引言
卷积神经网络最早是由Yann Lecun 提出用于手写数字识别,近年来在语音识别,自然语言处理等方面,均取得重大突破 [1] 。卷积神经网络在传统神经网络的基础上,最重要的改进是局部感知、权值共享,卷积神经网络中的卷积层有若干个特征地图(Feature Map)构成 [2] 。每个feature map由若干神经元组成,代表着提取出的图像特征,这些神经元通过同一个卷积核(权值)去卷积图像而获得,即这些同一个feature map共享同一组权值,权值共享机制大大减少了神经网络需要训练的参数量级,例如识别一个1000 × 1000的图像,假设隐藏层有1 M即106个神经元,那么传统神经网络采用全连接方式需要训练的参数个数为106 × 1000 × 1000,即1012 (2 G)个参数,显然这个计算数量级非常庞大。而采用卷积神经网络,假设同样设置隐藏层有1 M个神经元,每个神经元采用10 × 10大小卷积核去感知图像的固定区域,那么这种方式需要训练的参数为106 × 10 × 10,即108 (100 M)个参数,卷积神经网络局部连接的算法,一方面降低了需要训练的参数量级,另一方更符合人类神经对于图像的认知,即先感知局部,再到全局 [3] 。
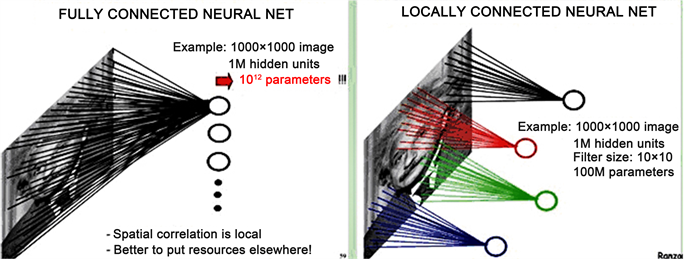
Figure 1. Local perception schematic of convolutional neural network
图1. 卷积神经网络局部感知示意图
卷积神经网络的第二个重要特性是权值共享 [4] ,图1中采用局部连接仍然需要训练100 M个权值参数,如果这1 M个神经元共享同一个10 × 10的卷积核,那么这1 M个神经元仅需要训练10 × 10个权值参数,这将极大的优化计算过程,这个10 × 10的卷积核相当于一种特征提取器,提取出的1 M个神经元即为一种feature map,通过不同的卷积核即可提取出图像的不同特征,综合到全局 [5] 。
由于卷积核比较小,卷积后得到的feature map仍然很大,为了降低图像维度,防止过拟合,采用池化即下采样的方法进行处理。池化的方法通常有:最大值下采样(Max-Pooling)与平均值下采样(Mean-Pooling),例如一个1000 × 1000的feature map 用一个100 × 100的采样窗口进行下采样,那么池化后的feature map大小为10 × 10。
例如图2所示,卷积层通过不同的卷积核识别出图像的不同特征,经过6层的特征提取提取和3次池化,最终由全连接层进行分类。
针对传统神经网络的计算复杂、缺少权值共享等问题,本文致力于讨论性能更优的卷积神经网络,在MATLAB中实现推导,并优化学习算法。

Figure 2. Calculation schematic of convolutional neural network
图2. 卷积神经网络计算示意图
2. 卷积神经网络的卷积核传递
一个传统神经网络的BP过程:先求出各个神经元的灵敏度函数,然后再求得误差函数对权值的导数,这个导数即为权值下降的梯度 [6] 。
首先,我们需要定义一个优化的目标函数:
(1)
为输出层第j个神经元的实际值,
为第j个神经元的理想值,采用方程(1)的形式定义目标函数,方便后面的求导计算:
(2)
首先求输出层神经元的误差:
(3)
代表第L层,即输出层第j个神经元,
为神经元
通过激活函数
后的激活值,那么即可求出输出层第j个神经元的误差为:
(4)
输出层之前的神经元误差可以由后一层逐层推算,
(5)
其中,
是
层第k个神经元,
是
层第k个神经元的误差。
由于
(6)
所以
(7)
因此
(8)
由上面推导过程可以求得每个神经元误差。权值更新需要求代价函数对权值的导数:
(9)
代价函数对偏置
的导数为:
(10)

Figure 3. The update process of the neural network weight
图3. 神经网络的权值更新过程
图3即为更新过程,类比于普通神经网络的神经元误差传递,卷积神经网络卷积层神经元误差传递为:
(11)
卷积层神经元误差在MATLAB中可以通过以下代码实现:
for j = 1 : numel(net.layers{l}.a)
net.layers{l}.d{j} = net.layers{l}.a{j} .* (1 - net.layers{l}.a{j}) .* (expand(net.layers{l + 1}.d{j}, [net.layers{l + 1}.scale net.layers{l + 1}.scale 1]) / net.layers{l + 1}.scale ^ 2);
end
net.layers{l}.a为第1层神经元,numel(net.layers{l}.a为卷积层神经元的个数,这里net.layers{l}.a{j} .* (1 - net.layers{l}.a{j})是对激活函数f(z)求导。expand(net.layers{l + 1}.d{j}, [net.layers{l + 1}.scale net.layers{l + 1}.scale 1]) / net.layers{l + 1}.scale ^ 2是上采样操作。
由于池化层神经元没有经过激活函数,神经元误差不需要对激活函数求导,所以池化层神经元误差传递公式为:
(12)
池化层神经元的误差在MATLAB中的实现方式为:
for i = 1 : numel(net.layers{l}.a)
z= zeros(size(net.layers{l}.a{1}));
for j = 1 : numel(net.layers{l + 1}.a)
z = z + convn(net.layers{l + 1}.d{j}, rot180(net.layers{l + 1}.k{i}{j}), 'full');
end
net.layers{l}.d{i} = z;
end
numel(net.layers{l}.a)为池化层神经元的个数,numel(net.layers{l + 1}.a)为池化层下一层即卷积层神经元的个数,net.layers{l}.d{i}为池化层第1层第i个神经元的误差。
在求得池化层核卷积层神经元误差后,下一步需要求得代价函数对网络权值的导数:
由于池化层没有进行权值加成,因此仅对卷积层进行权值梯度计算:
卷积神经网络的权值误差为:
(13)
(14)
卷积核和偏置的误差计算在MATLAB的实现方式为:
for j = 1 : numel(net.layers{l}.a)
for i = 1 : numel(net.layers{l - 1}.a)
net.layers{l}.dk{i}{j}=convn(flipall(net.layers{l-1}.a{i}),net.layers{l}.d{j},'valid')/size(net.layers{l}.d{j}, 3);
net.layers{l}.db{j} = sum(net.layers{l}.d{j}(:)) / size(net.layers{l}.d{j}, 3);
end
numel(net.layers{l}.a 为卷积层l神经元的个数,net.layers{l}.dk{i}{j}为第l层卷积核k{i}{j}的误差。net.layers{l}.db{j}为卷积层偏置的误差。
3. 深度学习算法优化
神经网络的非线性建模能力通过神经元的激活函数实现,深度学习使用的广泛的激活函数是tanh函数 [7] :
(15)
激活函数tanh的图像如图4所示,可以看出该函数处处可导,但是当输入
时,tanh导数激活为零,即处于饱和状态,神经元的参数更新的梯度非常小,这就导致神经元的误差传递效率几乎为零。为了避免梯度消失,在tanh函数叠加一个系数kx。
函数
,当输入
时,导数不为零,即可增加一个梯度k。优化后的tanh函数如图5所示,可以看到梯度明显增加,且不同k值会对梯度产生影响。

Figure 4. Primitive function and derived function of the tanh
图4. tanh的原函数和导数
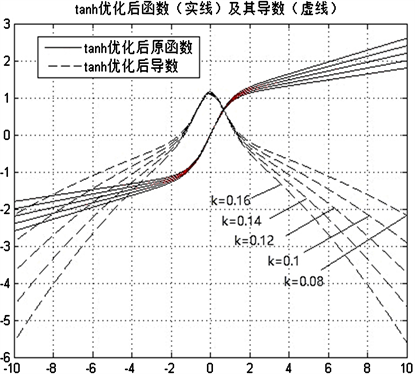
Figure 5. Primitive function and derived function of the optimized tanh
图5. 优化后tanh的原始函数及其导数
图6是优化后的激活函数,可以看出当k = 0.13时,误差降低速率最快,最终迭代后的误差值为:0.1694,在激活函数优化后,可避免梯度的消失,但是600迭代后,残差仍然有0.1694,需要通过修改学习速率来降低残差。图7是学习速率α分别取0.1,1.5,2,3,4,5时,误差的下降速度。当学习速率取2时,误差下降最快,残差值降低至0.0481。因此,在激活函数参数和学习速率要同时考虑时,才能取到参数的最优值。
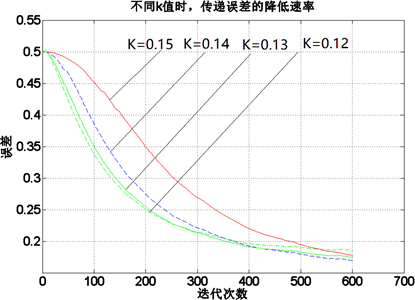
Figure 6. The influence of different k values on the calculation rate of error function
图6. 不同k值对误差函数计算速率的影响

Figure 7. Error reduction in different learning rates
图7. 不同学习速率的误差降低情况
Tanh激活函数在求导计算时,涉及指数运算,在处理大规模数据输入时,时间代价较大,为了更加快速地进行误差传递,采用
即Relu函数激活 [8] [9] ,该激活函数及其导数的图像如图8所示。从图中可以看出,当输入大于0时,其梯度快速增加,解决梯度消失问题,提供神经网络稀疏表达能力,但是当输入小于0时,梯度为0,在训练过程中权值无法更新,造成部分神经元死亡。为了解决这一问题,需要对max(0, x)激活函数进行改进。为了避免梯度消失的情况出现,将激活函数小于0范围内,增加一个修正系数α,即:
。既修正了数据分布,又保留了一些负轴的值,使得负轴信息不会全部丢失,但是修正系数α的选择无法直接确定。为了获得合适的修正系数,对于特定的神经网络,设置同样的修正系数进行训练。图9是采用不同的修正系数来训练同一个神经网络的输出结果。α = 0的情况即为max(0,x)激活函数的训练情况,其误差函数下降速度最缓,部分神经元已经死亡。增加修正系数后,误差函数下降明显提速,说明修正系数有效避免激活函数梯度消失的区间。为了获得更优的修正系数,继续增加修正系数的值,进行训练,从训练结果来看,当系数增加到0.06,误差函数的下降梯度变缓,因此,通过6组实验数据的训练曲线来看,修正系数α取0.05时,训练效果最佳。
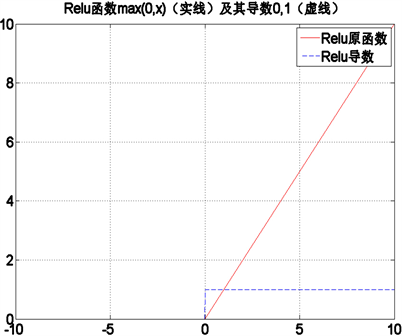
Figure 8. Primitive function and derived function of the Relu
图8. Relu的原函数和导数

Figure 9. Selection of correction coefficient
图9. 修正系数选择
4. 总结
讨论深度学习网络的误差传递计算过程,应用matlab建立深度学习网络对手写体进行识别,分析激活函数梯度饱和问题,优化激活函数,解决误差传递过程中梯度消失问题,通过计算得出最优的激活函数。通过对不同学习速率系数的计算,得出最优学习速率系数,在600次迭代中,使得神经网络的残差从0.169降低到0.0481。
本文讨论卷积神经网络算法的参数优化和算法的MATLAB实现,对以后深度学习尤其是在图像识别方面的应用具有一定的价值。